 |
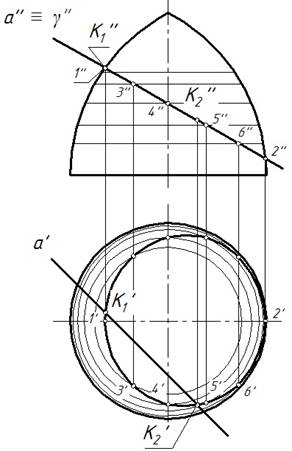
Последовательность построения точек пересечения прямой и поверхности.
|
|
|
|
Последовательность построения точек пересечения прямой и поверхности.
Последовательность построения аналогична задаче пересечения прямой с плоскостью:
1) γ - вспомогательная проецирующая плоскость;
2) прямаяа включена вγ ;
3) плоскость α пересекает поверхность по кривой (1 – 3 – 2);
4) кривая (1 – 3 – 2) пересечена прямой a в точках K1иK2.
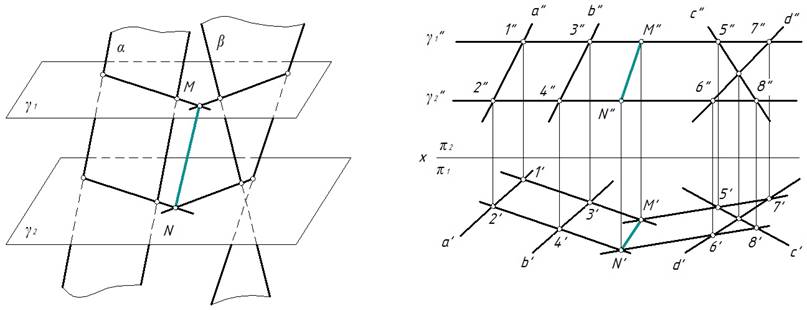
Последовательность построения линии пересечения двух плоскостей.
α ∩ β → l1, l2 …
вводим ɣ i – вспомогательные поверхности;
α ∩ γ i → mi; β ∩ γ i → ni; - строим линии пересечения с данной плоскостью
m i ∩ ni (т. к. лежат в одной поверхности γ i)
m i ∩ ni → Ki;
K 1 UK2 UK3 … U Ki → li
Задача. Построить проекции линии пересечения плоскостей.
Последовательность построения линии пересечения двух поверхностей.
1. Введем вспомогательную поверхность
2. Строим линии пересечения с заданной поверхностью.
3. В пересечении построенной линии получаем искомые точки пересечения
4. Объединяем точки в линии

Какая линия поверхности вращения называется ее меридианом?
Меридиан — линия полученная рассечением поверхности вращения плоскостью проходящей через её ось.

Какая линия поверхности вращения называется ее параллелью?
Параллель — окружность образованная вращением точки вокруг оси.

Правило построения проекций точки, принадлежащей поверхности вращения? Приведите пример.
Проекции точек строят с помощью окружностей (или образующих), принадлежащих поверхности вращения.
Какие конические сечения Вы знаете? При каком положении секущей плоскости относительно оси поверхности конуса сечением является эллипс? Приведите пример.
|
|
|
Конические сечения: эллипс, парабола, гипербола.


Какие конические сечения Вы знаете? При каком положении секущей плоскости относительно оси поверхности конуса сечением является парабола? Приведите пример.
Конические сечения: эллипс, парабола, гипербола.

Какие конические сечения Вы знаете? При каком положении секущей плоскости относительно оси поверхности конуса сечением является гипербола? Приведите пример.
Конические сечения: эллипс, парабола, гипербола.

Способы преобразования. Условия преобразования способом замены плоскостей проекций.
1. Положение фигуры неизменно
2. Изменяется положение первой из двух плоскостей проекции
3. Новая плоскость проекции перпендикулярна оставшейся
4. Положение новой плоскости может быть задано или выбрано.
Способы преобразования. Условия преобразования способом плоскопараллельного перемещения.
Плоскопараллельным перемещением геометрической фигуры в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельных друг другу плоскостях. При этом строятся новые проекции фигуры в частном положении по отношению к прежним плоскостям проекции.
Рассмотрим плоскопараллельное перемещение на примере рис. 5. 15 — преобразования прямой общего положения в прямую уровня — фронталь. Выполним плоскопараллельное движение прямой АВ относительно горизонтальной плоскости проекций П1. Точки А и В перемещаются в горизонтальных плоскостях. Суть построений заключается в том, что мы перемещаем проекцию А1В1 так, чтобы она стала параллельна оси П1/П2 и затем достраиваем проекцию A2'B2' на П2. Таким образом мы получаем ту же прямую, но перемещенную в новое состояние параллельное П2.
Алгоритм графических построений:
Из произвольной точки A1' параллельно оси П1/П2 откладываем расстояние равное длине проекции А1В1;
|
|
|
Проводим линии проекционной связи с П1 на П2.
Проводим вспомогательные горизонтальные линии на П2. Эти линии являются следами горизонтальных плоскостей, в которых перемещаются точки A и B;
Находим проекцию A2'B2' прямой A'B' на П2, как точки пересечения линий связи с горизонтальными линиями.

Прямая AB спроецировалась на П2 в натуральную величину, так как она параллельна ей. При перемещении угол а наклона AB к П1 не изменился, так как перемещение происходило в горизонтальной плоскости. И теперь его можно определить по полученной проекции A2'B2' на П2.
|
|
|


