 |
II . 2. Показательная функция и ее свойства.
|
|
|
|
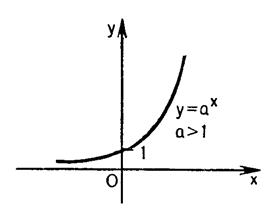 Функция, заданная формулой вида у = ах, где а — некоторое положительное число, не равное единице, называется показательной.
Функция, заданная формулой вида у = ах, где а — некоторое положительное число, не равное единице, называется показательной.
1.Функция у = ах при а>1 обладает следующими свойствами (см. рис. II.7.):
а) область определения — множество всех действительных чисел;
б) множество значений — множество всех положительных чисел;
Рис. II.7.
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если x > 0, то а x > 1;
е) если х < 0, то 0 < ах < 1.
3. Функция у = ах при 0<а< 1 обладает следующими свойствами (см. рис. II.8.):
 а) область определения D (f)= R;
а) область определения D (f)= R;
б) множество значений E (f)= R +;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0 < ах < 1;
е) если х < 0, то ах > 1.
Рис. II.8.
Глава III. Решение показательно-степенных уравнений, алгоритмы и примеры.
Так называются уравнения вида  , где неизвестное находится и в показателе и в основании степени.
, где неизвестное находится и в показателе и в основании степени.
Можно указать совершенно четкий алгоритм решения уравнении вида  . Для этого надо обратить внимание на то, что при а(х) не равном нулю, единице и минус единице равенство степеней с одинаковыми основаниями (будь-то положительными или отрицательными) возможно лишь при условии равенства показателей То - есть все корни уравнения
. Для этого надо обратить внимание на то, что при а(х) не равном нулю, единице и минус единице равенство степеней с одинаковыми основаниями (будь-то положительными или отрицательными) возможно лишь при условии равенства показателей То - есть все корни уравнения  будут корнями уравнения f (x) = g (x) Обратное же утверждение неверно, при а(х) < 0 и дробных значениях f (x) и g (x) выражения а(х) f ( x ) и
будут корнями уравнения f (x) = g (x) Обратное же утверждение неверно, при а(х) < 0 и дробных значениях f (x) и g (x) выражения а(х) f ( x ) и
а(х) g ( x ) теряют смысл. То - есть при переходе от 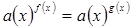 к f (x) = g (x) (при
к f (x) = g (x) (при 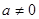 и
и 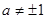 могут появиться посторонние корни, которые нужно исключить проверкой по исходному уравнению. А случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно.
могут появиться посторонние корни, которые нужно исключить проверкой по исходному уравнению. А случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно.
Итак, для полного решения уравнения  рассматриваем случаи:
рассматриваем случаи:
1. а(х) = О. Если при значении х, удовлетворяющем этому уравнению, f (x) и g { x) будут положительными числами, то это решение. В противном случае, нет
|
|
|
2. а(х) = 1. Корни этого уравнения являются корнями и исходного уравнения.
3. а(х) = -1. Если при значении х, удовлетворяющем этому уравнению, f (x) и g (x) являются целыми числами одинаковой четности (либо оба четные, либо оба нечетные), то это решение. В противном случае, нет
4. При 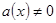 и
и 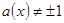 решаем уравнение f (x)= g (x) и подстановкой полученных результатов в исходное уравнение отсекаем посторонние корни.
решаем уравнение f (x)= g (x) и подстановкой полученных результатов в исходное уравнение отсекаем посторонние корни.
Примеры решения показательно-степенных уравнений.
Пример №1.
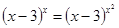
Решение
1) x – 3 = 0, x = 3. т.к. 3 > 0, и 32 > 0, то x1 = 3 - это решение.
2) x – 3 = 1, x2 = 4.
3) x – 3 = -1, x = 2. Оба показателя четные. Это решение x3 = 1.
4) x – 3 ≠ 0 и x ≠ ± 1. x = x2, x = 0 или x = 1. При x = 0, (-3)0 = (-3)0 –верно это решение x4 = 0. При x = 1, (-2)1 = (-2)1 – верно это решение x5 = 1.
Ответ: 0, 1, 2, 3, 4.
Пример №2.

Решение
По определению арифметического квадратного корня: x – 1 ≥ 0, x ≥ 1.
1) x – 1 = 0 или x = 1,  = 0, 00 это не решение.
= 0, 00 это не решение.
2) x – 1 = 1 x 1 = 2.
3) x – 1 = -1 x 2 = 0 не подходит в ОДЗ.
4)  =
= 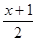
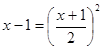
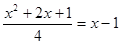
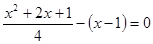


Д = (-2) – 4*1*5 = 4 – 20 = -16 – корней нет.
Ответ: 2.
Пример №3.
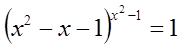
Решение
1) 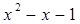 = 0 решения нет, т.к. 0 в любой степени не равен 1.
= 0 решения нет, т.к. 0 в любой степени не равен 1.
2) 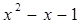 ≠ 0 т.е.
≠ 0 т.е.  . Тогда можем записать:
. Тогда можем записать:

3) 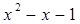 = 1.
= 1. 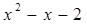 = 0
= 0
 и
и 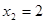
4) 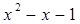 = -1 х = 0 или х = 1. При х = 0
= -1 х = 0 или х = 1. При х = 0 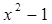 = -1. (-1)-1 ≠ (-1)0. Это не решение. При х = 1 (-1)0 = (-1)0. Это решение х3 = 1.
= -1. (-1)-1 ≠ (-1)0. Это не решение. При х = 1 (-1)0 = (-1)0. Это решение х3 = 1.
5) 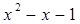 ≠ 0 и
≠ 0 и 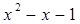 ≠ ±1 имеем
≠ ±1 имеем 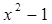 = 0,
= 0, 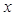 = -1 или
= -1 или
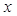 = 1. Эти корни уже учтены.
= 1. Эти корни уже учтены.
Ответ: -1, 1, 2.
Пример №4.
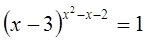
Решение
1) При  решений нет, т.к. 0 в любой степени не равен 1.
решений нет, т.к. 0 в любой степени не равен 1.
при 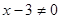 ,
, 
2)  ,
, 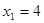 .
.
3)  ,
,  .
.
 , (-1)0 = (-1)0 это решение.
, (-1)0 = (-1)0 это решение.
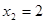 .
.
4)  и
и 

 или
или 
При  (-4)0 = 1 – верно.
(-4)0 = 1 – верно. 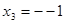
Ответ: -1, 2, 4.
Пример №5.

Решение
1) 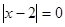 ,
,  ,
, 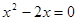 это не решение.
это не решение.
2)  ,
, 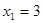 и
и  .
.
3) отрицательных значений основание не имеет. При  и
и 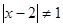 ,
, 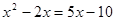 ,
,  ,
,
х = 5, 315 = 315 – верно. х3 = 5,
х = 2 – не является решением.
Ответ: 1,3,5.
Пример №6
|
|
|

Решение
1)  не дает решений, т.к. 0 ни в какой степени не равен 1.
не дает решений, т.к. 0 ни в какой степени не равен 1.
2)  .
.  или
или 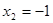 .
.
3) отрицательных значений 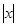 не имеет.
не имеет.
4) При  ,
, 
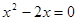 , т.к.
, т.к.  , то
, то  . Проверка 20 = 1 – верно.
. Проверка 20 = 1 – верно. 
Ответ: -1, 1, 2.
Пример №7
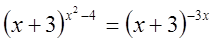
Решение
1) 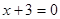 ,
,  ,
, 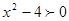 ,
,  . Это решение
. Это решение  .
.
2)  ,
,  .
.
3) 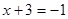 ,
, 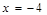 ,
, 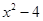 - четное и -3х – четное. Это решение. х2 = -4.
- четное и -3х – четное. Это решение. х2 = -4.
4)  и
и 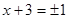 ,
,  ,
,  ,
, 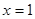 , 4-3 = 4-3 – верно.
, 4-3 = 4-3 – верно.  .
.
Ответ: -4, -3, -2, 1
Пример №8

Решение
ОДЗ: 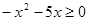 ,
, 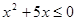
 ,
,  ,
,
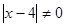 и
и 

Все решения принадлежат уравнению 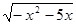 =2.
=2.
 ,
, 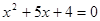 ,
,  и
и 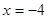 . Оба значения принадлежат к ОДЗ.
. Оба значения принадлежат к ОДЗ.
Ответ: -4, -1.
Пример №9

Решение
ОДЗ:  ,
,  ,
,  .
.
1) 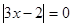 решений не имеет, т.к. 0 в любой степени не равен 1.
решений не имеет, т.к. 0 в любой степени не равен 1.
При 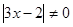 ,
,  или
или  ,
,
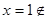 ОДЗ,
ОДЗ,  ОДЗ.
ОДЗ.
Значит все решения содержатся в уровнении  = 0,
= 0,  или
или 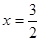 .
.
Проверка:  , 20 = 1 – верно.
, 20 = 1 – верно.
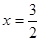 ,
, 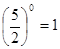 - верно.
- верно.
Ответ: 0, 3/2.
Пример №10

Решение
1)  решений не дает, т.к. 0 в любой степени не равен 1.
решений не дает, т.к. 0 в любой степени не равен 1.
2) При 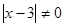 ,
,  ,
,  . Все решения принадлежат уравнению
. Все решения принадлежат уравнению  .
.  или
или 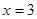 .
.
3) 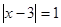 ,
, 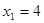 и
и 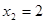 .
.
Второе решение не подходит, т.к 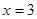 ,
, 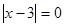 . А
. А  является решением
является решением 
Ответ:  , 2, 4.
, 2, 4.
Пример №11

Решение
1) 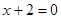 ,
, 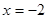 ,
, 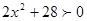 и
и 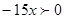 это решение
это решение  .
.
2) 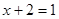 ,
,  .
.
3)  ,
, 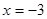 ,
, 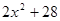 - четное,
- четное,  - нечетное. Это является решением.
- нечетное. Это является решением.
4) 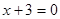 или
или  ,
,  ,
,  ,
, 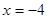 ,
, 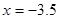 .
.
Проверка:  ,
,  - верно.
- верно.
Но 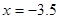 не является корнем!
не является корнем!
Выражение (-1,5)52,5, которое получается при проверке не имеет смысла, т.к. степень отрицательно числа имеет смысл только для целых показателей. Равенство  =
= 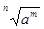 только для
только для  . Значит, отрицательное число можно возводить только в степень с целым показателем.
. Значит, отрицательное число можно возводить только в степень с целым показателем.
Ответ: -4, -2, -1.
Пример №12

Решение
ОДЗ:  . Значит 0,1 и -1 отпадают.
. Значит 0,1 и -1 отпадают.
 и все решения содержатся в уравнении.
и все решения содержатся в уравнении.
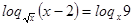
 ,
, 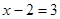 ,
, 
Ответ: 5.
Пример №13

Решение
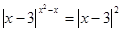
1) 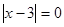 ,
,  ,
,  . Это решение
. Это решение  .
.
2)  ,
, 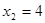 ,
,  .
.
3) отрицательных значений 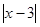 не имеет.
не имеет.
При 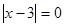 или
или 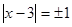 все решения в уравнении
все решения в уравнении 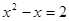 ,
, 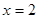 и
и 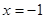 .
.
При 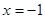 ,
,  - верно.
- верно. 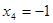 .
.
Ответ: -1, 2, 3, 4.
Пример №14
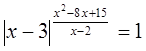
Решение
ОДЗ: 
1) При 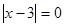 решений нет, т.к. 0 в любой степени не равен 1.
решений нет, т.к. 0 в любой степени не равен 1.
При 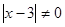
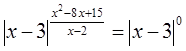
2)  ,
,  и
и 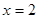 .
. 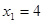 - решение, а
- решение, а 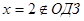 .
.
3) 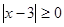 для всех
для всех  . При
. При 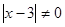 и
и 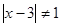 все решения содержатся в уравнении
все решения содержатся в уравнении  ,
, 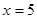 или
или  . При
. При  ,
, 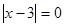 .
.
При 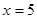 ,
, 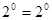 - верно.
- верно. 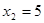 .
.
Ответ: 4, 5.
Пример №15.
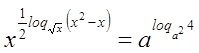 ,
, 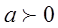
Решение

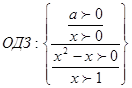
используя свойства логарифма  и
и 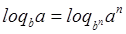 получили:
получили:
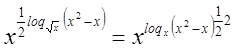 =
= 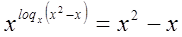
В первой части уравнения выполнили преобразования
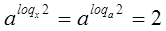 . Получили уравнение
. Получили уравнение  . Все решения содержатся в уравнении.
. Все решения содержатся в уравнении.
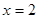 или
или 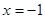 .
. 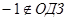
Ответ: 2.
Пример №16

Решение
ОДЗ: 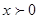
Преобразуем знаменатель дроби в правой части уравнения
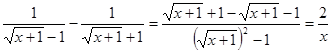 ;
;  .
.
 ,
, 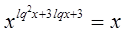 , где
, где 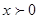
|
|
|
1) 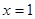 ,
, 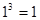 - верно.
- верно.
2)  ,
, 
Пасть  , тогда
, тогда 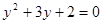

 ,
, 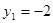 или
или 
 .
.
Следовательно; 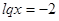 или
или  ,
,  ,
,  .
.
Ответ: 1, 0,1, 0, 0,01.
Пример №17

Решение
ОДЗ:  и
и 
Выполним преобразования.
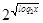 +
+ 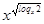 = 2+2
= 2+2
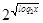 +
+ 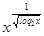 = 4
= 4
Пусть 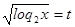 , а
, а 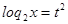 ,
, 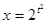
Следовательно,  или
или
 ,
, 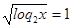
2*2t = 4 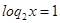
2t = 4/2 
2t = 2
t = 1
Ответ: 2.
Пример №18
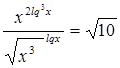
Решение
ОДЗ: 
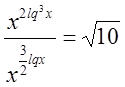 ;
; 
Прологарифмируем обе части равенства:
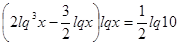
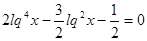 , где
, где 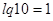 .
.
Умножим обе части уравнения на 2.
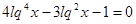
Пусть 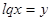 , тогда
, тогда 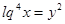


 ,
, 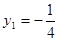 или
или 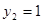
1)  ,
, 
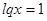 или
или 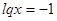


Ответ: 0.1, 10.
Пример №19

Решение
ОДЗ: 
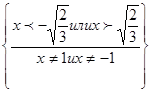
Обратите внимание 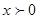 ниоткуда не следует! Наоборот, из ОДЗ видно, что
ниоткуда не следует! Наоборот, из ОДЗ видно, что  может быть отрицательным!
может быть отрицательным!

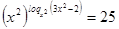 ,
, 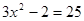
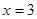 или
или 
Оба значения в ОДЗ.
Так как возводили в квадрат, корни надо проверить.
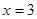 ,
, 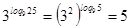 - верно.
- верно.
 ,
, 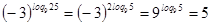 - верно.
- верно.
Ответ: -3, 3.
Пример №20
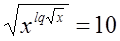
ОДЗ: 
Возведем обе части уравнения в квадрат (т.к. они положительны, то посторонние корни не появляются)
 или
или 
Прологарифмируем по основанию 10.

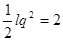 или
или 
1)  или
или 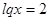
 ,
, 
Ответ: 0.01, 100.
Пример №21

Решение
ОДЗ: 
Прологарифмируем по основанию 10.
 , где
, где 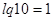 .
.

Пусть  , тогда:
, тогда:
 умножим на 4
умножим на 4
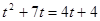
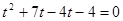 ,
, 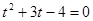
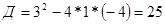
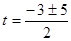 ,
, 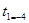 или
или 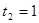
1) 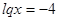
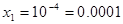
2) 

Ответ: 0,0001, 10.
Пример №22
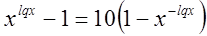
Решение
ОДЗ: 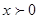

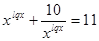
Заменим:  , получим:
, получим:
 , где
, где 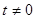 .
.
Решаем уравнение: 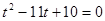
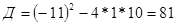
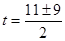 ;
; 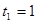 или
или 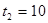
1) 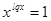 ;
;  ;
; 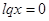 .
.  .
.
2) 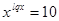 ,
,  ,
, 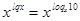 ,
,  ,
,  .
.
 ;
;  ;
; 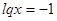 ;
;  .
.
Ответ: 0,1, 1, 10.
Пример №23

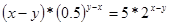

Решение
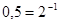 и
и 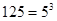
 \:
\: 
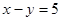
Подставим во второе уравнение вместо  число 5, получим:
число 5, получим:
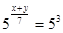
 или
или 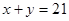
составляем систему уравнений:
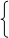
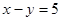
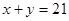

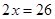

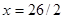


Ответ: (13;8)
Пример №24

Решение
ОДЗ: 

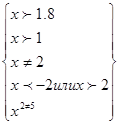

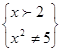
 ;
; 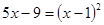
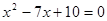 ,
,
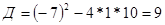
 ;
; 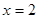 или
или 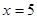
 ,
, 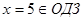 .
.
Ответ: 5.
Пример №25

Решение
ОДЗ: 
Прологарифмируем правую и левую части данного уравнения по основанию 10:
Получим:
 или
или 
Обозначив  , перепишем записанное уравнение в виде:
, перепишем записанное уравнение в виде:
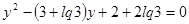 .
.
Решая его относительно 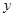 , находим
, находим 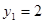 ,
,  .
.
Используя обозначения  , из первого решения квадратного уравнения имеем
, из первого решения квадратного уравнения имеем 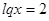 . Отсюда
. Отсюда  . Используя решение
. Используя решение  , получаем
, получаем  . Преобразуем правую часть этого уравнения:
. Преобразуем правую часть этого уравнения:
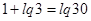 . Значит,
. Значит, 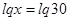 , т.е.
, т.е.  .
.
Ответ: 30, 100.
Пример №26
|
|
|

Решение
Так как 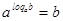 , то при
, то при  и
и  имеем равносильное уравнение:
имеем равносильное уравнение:
 или
или 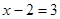
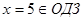 .
.
 ,
, 
Ответ: 5.
Пример № 27
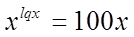
Решение
ОДЗ: 
Так как обе части уравнения положительны, то прологарифмируем по основанию 10:


 ,
, 

 ;
;  или
или 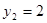
1)  2)
2) 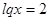
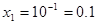

Ответ: 0.1, 100.
Пример №28
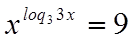
Решение
ОДЗ: 
Так как обе части уравнения положительны, то прологарифмируем по основанию 3:
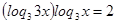
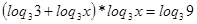
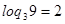 и
и 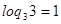 , поэтому
, поэтому
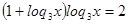

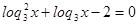
Пусть  , тогда
, тогда 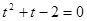
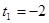 или
или 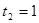 .
.
1) 
 ;
;
2) 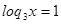
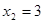
Ответ:  , 3.
, 3.
Пример №29

Решение
1) 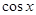
 , т.к. 0 в любой степени не равен 1.
, т.к. 0 в любой степени не равен 1.
2)  = 1,
= 1, 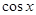 =1,
=1,  ,
,  или
или
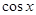 =-1,
=-1,  ,
,  .
.
Так как 1 в любой степени равна 1, то это решения.
3) 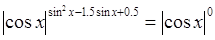 (т.к.
(т.к.  )
)
При  все решения принадлежат уравнению
все решения принадлежат уравнению 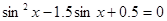 .
.  или
или  .
.
При 

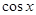 = 0, что не удовлетворяет уравнению
= 0, что не удовлетворяет уравнению 

 ,
, 
Ответ: 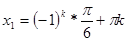 ,
, 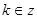 .
.
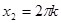 ,
,  .
.
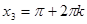 ,
,  .
.
Пример №30

Решение
ОДЗ: 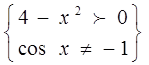

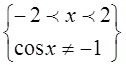
 =
= 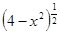
1)  ,
, 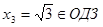 ,
, 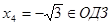 .
.
2) Так как  , то остальные решения получаем из уравнения
, то остальные решения получаем из уравнения  : Отсюда
: Отсюда  или
или 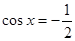 .
. 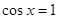
 ,
,  и
и 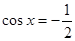

 ,
, 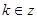 .
.
Ответ:  , -
, - 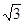 ,
,  и
и  ,
, 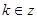 .
.
Пример №31

Решение

1) 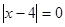 или
или  ,
,  и
и


