Силы вредных сопротивлений

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра «Механическое оборудование

И детали машин»

 

СИЛОВОЙ АНАЛИЗ

РЫЧАЖНЫХ МЕХАНИЗМОВ

 

Методические указания

По теории механизмов и машин

 

М о с к в а 2 0 14

 

Цель силового анализа

Целью силового анализа (расчета) рычажного механизма является: 1) определение действующих на звенья механизма сил при заданном движении механизма; 2) определение реакций в кинематических парах; 3) определение уравновешивающей силы или уравновешивающего момента, приложенных к ведущему звену механизма.

Силовой анализ начинают с составления расчетной схемы: рисуют метрическую* схему механизма с указанием приложенных к звеньям внешних сил, часть из которых может быть задана, а часть подлежит определению. В связи с этим рассмотрим силы, которые могут участвовать в силовом расчете.

Классификация и характеристика сил

Силы движущие

Эти силы, считающиеся в ТММ известными и создающими положительную работу, приводят механизм в движение, т. е. эти силы создаются двигателем и определяются, например, его механической характеристикой.

Силы полезного сопротивления

Эти силы, как и силы движущие, в ТММ считаются известными: они обычно задаются в техническом задании на проектирование машины. Силы полезного сопротивления определяются назначением механизма и тем технологическим процессом, в котором он используется, например, силы сопротивления резанию ковшом экскаватора или силы резания для токарного станка.

Силы вредных сопротивлений

Эти силы в механизмах и машинах строительной отрасли чаще всего проявляются в виде сил трения и сил сопротивления внешней среды.

В плоских рычажных механизмах силы трения проявляются в низших одноподвижных кинематических парах пятого класса (поступательные, вращательные и винтовые) и в высших двухподвижных кинематических парах четвертого класса (например, контакт зубьев в зубчатом зацеплении или контакт ролика с кулачком).

Разберем силы трения в низших и высшей кинематических парах.

В поступательной паре (рис. 1) сила трения F_тр равна произведению силы нормального давления N на коэффициент трения скольжения f и направлена в сторону противоположную движению данного тела.

На рис. 1 к ползуну под углом a приложена движущая сила F_д, которую перенесли в точку А и разложили на две составляющие: вертикальную F_в = F_д cosa и горизонтальную F_г = F_д sina. Кроме того, к телу со стороны направляющей приложена нормальная реакция N=F_в=F_д cosa и сила трения F_тр = N∙f.

Сумма сил N и F_тр дает полную реакцию поверхности R, отклоненную от вертикали на угол трения j:

tg j arctg f.

Из схемы рис. 1 можно установить, что движение возможно при F_г > F_тр или

F_д sina > F_д cosa∙ f; => tga > tgj;

a > j.

 

Если движущая сила F_д будет приложена к телу под углом

a £ j, то какой бы величины она ни была, эта сила не сможет сдвинуть тело. Такое явление называется самоторможением и широко используется в технике, например, в крепежных резьбах.

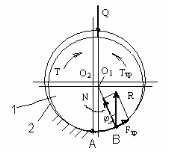
Во вращательной паре (рис. 2) движению (вращению) одного звена (пальца 1) относительно другого (втулки 2) под действием вращательного момента Т мешает момент трения

Т_тр = F_тр × r ₁ = R ∙ f ×r₁ = Q ∙ f ∙ r,

 

где Q – внешняя нагрузка на вращательную пару; f – коэф-

фициент трения скольжения контактирующих поверхностей; R = Q – полная реакция поверхности, отклоненная от нормали N на угол трения j; r – номинальный радиус вращательной пары; r ₁ – радиус пальца*.

На рис. 2 также показано, что контакт тел из точки А при покое перемещается в точку В при движении, где и возникают указанные выше силы. Приведенный коэффициент трения во вращательной паре больше, чем в поступательной на 25...50% в зависимости от степени приработанности поверхностей вращательной кинематической пары.

В винтовой кинематической паре действие сил между витками винта и гайки можно свести к действию сил на тело, находящееся на наклонной плоскости (рис. 3). Также можно допустить, что силы приложены по середине витка резьбы.

Схема рис. 3а составлена для случая подъема винта при прямоугольном профиле витка. Винтовая пара нагружена вертикальной (вдоль оси винта) силой Q, и винт вращается под действием момента Т, определяемого движущей силой F_д, приложенной к среднему радиусу резьбы r. Движению мешает сила трения в резьбе

F_тр = N × f,

где N – нормальная реакция поверхности,

f – коэффициент трения скольжения.

 

 

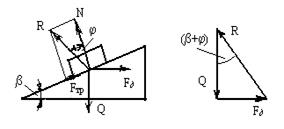
а б

 

Рис. 3. Трение в винтовой паре: а – расчетная схема; б – план сил

 

Полная реакция поверхности (равнодействующая сил N и F_тр) отклоняется от нормали N на угол трения j в сторону, противоположную движению. Рассматривая равновесие сил, приложенных к телу, из рис. 3,б найдем требуемую движущую силу

F_д = Q ×tg (b + j),

где b - угол подъема витка резьбы (угол наклона винтовой линии).

Тогда момент, необходимый для подъема винта

Т = F_д × r = Q × r ×tg(b + j).

В случае опускания этот момент

Т = Q × r ×tg (b – j).

В случае треугольного профиля витка резьбы (рис. 4), что характерно для крепежных резьб, сила трения определяется с учетом угла профиля резьбы a (для метрических резьб a=60°). Внешняя осевая сила Q разложена на две симметрично расположенные силы Q /2, уравновешиваемые двумя реакциями:

N = Q / (2cos (a/2)).

Тогда сила трения

Величина f * = f /cos(a/2) называется приведенным коэффициен­том трения, а угол трения j*= arctg(f *) называется приведенным углом трения. При β < φ* в винтовой паре обеспечивается самоторможение: никакая осевая сила не вызовет поворот винта.

Рис. 4. К определению силы трения в винтовой паре

с треугольным профилем витка

 

В высшей кинематической паре возможны поступательное и качательное (вращательное) движения одного звена относительно другого. Поэтому может проявляться как трение скольжения, так и трение качения. Первое мы уже разобрали и рассмотрим трение качения.

При перекатывании цилиндра (рис. 5) равнодействующая R сил реакции поверхности смещается относительно линии действия внешней прижимающей силы Q на величину k. Это смещение k называется плечом силы трения качения или коэффициентом трения качения и имеет размерность длины. Если цилиндр перекатывается под действием внешнего момента Т, то возникающее перекатыванию сопротивление в виде момента трения Т_тр £ Т будет равно

T_тр = Q × k.

Если внешний момент Т создается силой Р и Т = Р × r, где r - радиус цилиндра, то приведенный коэффициент трения скольжения найдем из условия равновесия при равномерном движении:

Т = Т_р; => Р × r = Q × k;

P = Q ,

где приведенный коэффициент трения скольжения.

Из последнего выражения следует важный вывод: с увеличением радиуса цилиндра приведенный коэффициент трения уменьшается, а, следовательно, уменьшаются и потери на трение качения.

Рис. 5. Трение качения в высшей

кинематической паре

4. Силы тяжести. Эти силы всегда направлены вертикально вниз и равны произведению массы тела m на ускорение свободного падения g:

Q = mg.

Они могут играть роль сил движущих или сил полезного сопротивления.

5. Силы инерции. Под силой инерции понимается вектор 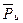, равный произведению массы на ускорение центра масс и направленный против ускорения центра масс:

где m - масса тела, - вектор ускорения центра масс.

При сложном движении тела (рис. 6), обладающего распределенной массой, в общем случае кроме силы инерции 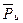, приложенной к центру масс, возникает момент от сил инерции или инерционный момент , приложенный к звену. Он равен произведению момента инерции звена Is относительно оси, проходящейчерез центр масс и перпендикулярной плоскости движения, на угловое ускорение этого звена и направлен в сторону противоположную угловому ускорению:

.

Действие силы инерции 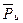и инерционного момента можно заменить действием одной силы инерции, смещенной параллельно самой себе на плечо h = / 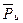так, чтобы момент результирующей силы инерции относительно центра масс был направлен против углового ускорения звена (рис. 6). Точка К, к которой приложена результирующая сила инерции, называется центр качания звена.

К рис. 6 можно сделать следующие пояснения.

1. При силовом расчете к звену прикладывают либо в центре масс S силу инерции 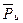и момент инерции , либо к центру качания звена в точке К только силу инерции .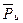

2. Полное ускорение центра масс звена при плоскопараллельном движении складывается из двух составляющих: нормальной характеризующей изменение скорости по направлению и направленной вдоль звена к центру вращения, и тангенциальной характеризующей изменение скорости по величине и направленной по касательной к траектории движения центра масс. Величина и направление углового ускорения звена определяется тангенциальной составляющей

6. Реакции в кинематических парах. Это силы взаимодействия звеньев. Если в кинематической паре соединены звенья i и j и звено i действует на звено j, то возникает реакция:

Обычно плоский механизм состоит из кинематических одноподвижных поступательных и вращательных пар и высшей двухподвижной пары.

В высшей паре (рис. 7,а) реакция 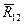или 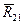возникает в точке соприкосновения тел А и направлена по общей нормали n-n к контактирующим поверхностям. То есть для высшей кинематической пары известно направление реакции и точка её приложения и неизвестен всего один параметр – величина реакции.

Во вращательной паре (рис. 7,б) реакция R ₁₂ проходит через центр шарнира В, но её величина и направление неизвестны, т. е. неизвестны два параметра.

 

В поступательной паре (рис. 7,в) реакция 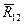перпендикулярна направляющей х-х,а ее величина и точка приложения неизвестны, т. е. как и в предыдущем случае неизвестны два параметра.

б

в

а

 

Рис. 7. Реакция в кинематических парах:

а – высшей; б – вращательной; в – поступательной

 

Таким образом, каждая высшая пара четвертого класса для определения реакции имеет одну неизвестную, а каждая низшая пара пятого класса – две неизвестные. Поэтому, если кинематическая цепь имеет число кинематических пар пятого и четвертого классов соответственно Р ₅ и Р ₄, то число неизвестных будет 2 Р ₅+ Р ₄. В то же время для этой цепи, состоящей из n звеньев, можно составить 3 n уравнений статического равновесия. Статическая определимость кинематической цепи возникает при равенстве числа неизвестных числу уравнений статики:

2 Р ₅ + Р ₄ = 3 n или 3 n – 2 P ₅ – P ₄ = 0,

а это является уравнением структурной группы. Поэтому, структурные группы являются статически определимыми, что и определяет порядок силового анализа.

ПОРЯДОК СИЛОВОГО РАСЧЕТА

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: