 |
Структурная группа звеньев 2-3
|
|
|
|
На рис. 11,а к звеньям приложена известная сила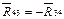 
, которую мы уже нашли из решения предыдущей структурной группы, и реакции отброшенных связей: 
и 
. Нормальная составляющая реакции направлена вдоль звеньев, а тангенциальная – перпендикулярно соответствующим звеньям.
Запишем векторное уравнение сил для этой структурной группы
+ 
+ 
+ 
+ 
= 0;
В этом уравнении полностью известна реакция , а все остальные известны только по направлению. Таким образом, имеются четыре неизвестных, две из которых – тангенциальные составляющие и - найдем аналитически из условия равенства нулю суммы моментов всех сил относительно внутренней кинематической пары C отдельно для каждого из звеньев, а две – нормальные составляющие и – из плана сил. Итак:
для 2-го звена: 
. 
∙ВС=0; => =0.
для 3-го звена: . 
∙СD-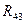 
∙ 
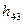=0; => 
.
а б
Рис. 11. Расчетная схема для структурной группы звеньев 2-3 (а)
и звена 2 (б)
Теперь строим план сил (рис. 12). Сначала чертим друг за другом в выбранном масштабе сил известные вектора и . Затем через конец вектора проводим направление нормальной составляющей , а через начало вектора направление нормальной составляющей . Точка пересечения этих направлений ограничивает соответствующие реакции. Стрелки ставим так, чтобы вектора шли один за другим.
Вектор одновременно является и полной реакцией 
, так как =0. По масштабу сил найдем числовое значение реакций.
Для нахождения реакции во внутренней кинематической паре необходимо рассмотреть равновесие одного из звеньев группы. В данном случае проще рассмотреть равновесие второго звена (рис. 11,б): в точке В приложена реакция , и для равновесия звена в точке С необходимо приложить 
.
|
|
|
Таким образом, найдены реакции во всех кинематических парах этой группы и можно перейти к ведущему звену.
Механизм первого класса
Структурная группа имеет степень подвижности W = 0 и она статически определима. Механизм 1-го класса имеет W = 1 и для статической определимости необходимо приложить к ведущему звену уравновешивающую силу Ру или уравновешивающий момент Му. Физически эту силу или момент развивает двигатель.
Уравновешивающая сила
Принято считать, что ее развивает зубчатая передача, приводящая кривошип в движение. Если нет дополнительных указаний, то уравновешивающую силу прикладывают к концу кривошипа и перпендикулярно кривошипу (рис. 13).
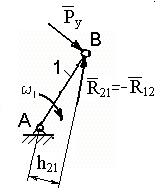
Рис. 13. Механизм 1-го класса Рис. 14. План сил для ведущего звена
Из условия 
найдем Ру:
Ру × АВ –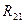 
∙ 
= 0; => 
.
Для определения реакции в опоре необходимо рассмотреть равновесие ведущего звена, заменив влияние опоры реакцией 
: векторная сумма всех сил должна быть равна нулю, т.е.
+ 
+ = 0.
В этом уравнении все слагаемые, кроме 
, полностью известны. Поэтому полную реакцию в кинематической паре А можно найти из плана сил рис. 14. Для его построения откладываем в выбранном масштабе сил одну за другой реакцию и уравновешивающую силу . Затем соединяем начало вектора с концом , получаем направление и с помощью масштаба величину реакции .
Уравновешивающий момент
Уравновешивающий момент Му может передавать приводная муфта, соединяющая двигатель или редуктор с кривошипом. Величину этого момента также, как в предыдущем случае уравновешивающую силу, находят из условия 
(рис. 15):
Му – R 21 ∙h 21 ∙ml = 0;=> My = R 21× h 21× ml.
Рис. 15. Механизм 1-го класса Рис. 16. Схема сил для ведущего звена
Здесь можно сделать два замечания: 1) если к звену приложен внешний момент, то в уравнении равновесия необходимо использовать истинные, т. е. физически существующие размеры. Поэтому появился сомножитель ml – масштаб длин; 2) из сравнения выражений для Ру и Му следует простая зависимость:
|
|
|
Му = Ру × lAB,
где lAB – истинный размер кривошипа.
Для определения реакции в опоре А рассмотрим равновесие сил, приложенных к ведущему звену (рис. 16):
+ = 0; => = – .
В данном случае мы сразу находим реакцию без построения плана сил.
Контрольные вопросы к защите
второго листа курсового проекта
1. Какова цель силового анализа механизма?
2. Каков порядок силового расчета и почему?
3. Из каких условий находят реакции в кинематических парах?
4. Как действия силы и момента инерции можно заменить действием одной силы инерции?
Библиографический список
Теория механизмов и механика машин: Учебник для вузов / Под ред. К.В. Фролова. М.: Изд-во МГТУ, 2009.
* Метрической называют схему механизма, выполненную в масштабе при известных размерах всех звеньев и взаимном расположении всех кинематических пар.
* Вращение пальца 1 с радиусом r 1 во втулке 2 с радиусом r 2 возможно при r 2 > r 1. Эти радиусы могут отличаться от номинального (расчетного) радиуса пары только в пределах допусков, поэтому в данном случае принимаем r 1 = r 2 = r, обеспечивающих соединение с зазором.
* Значение сил рекомендуем округлять до трех значащих цифр. Далее числовое значение сил приводить не будем, а выполним расчет в общем виде.
|
|
|
