Силовой линией или линией вектора напряженности поля называется линия, для которой направление касательной в любой точке совпадает с направлением вектора напряженности поля.

рисунок с силовыми линиями

Густота линий на рисунке пропорциональна величине вектора напряженности электрического поля. Силовые линии начинаются на положительных зарядах, а заканчиваются на отрицательных. Силовые линии нигде не пресекаются.

Электрическое поле, напряженность которого во всех точках одинаково называется однородным.

Силовые линии такого поля параллельны, а расстояние между ними – одинаково! Например, таким является поле внутри плоского конденсатора.

рисунок с конд.

Поле точечного заряда

Величина вектора 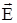поля точечного заряда определяется формулой (1.14).

(1.21)

рисунок

Диполь

Электрическим диполем (двойным полюсом) называется электрическая система, состоящая из двух зарядов +q и -q равных по величине, противоположных по знаку и находящихся на расстоянии r.

Электрическим моментом диполя или дипольным моментом называется вектор

,

где - радиус-вектор, проведенный от отрицательного заряда к положительному.

l - называется плечом диполя.

 

§9: Поток вектора и электростатическая теорема Гауса. Применение теоремы Гауса.

 

Понятие потока вектора является одним из важнейших понятий векторного анализа. Оно используется при формулировке важнейших свойств электрического, магнитного и других векторных полей. Первоначально это понятие было введено в гидродинамике.

рис.

 

Возьмем в поле скоростей движущейся жидкости малую (плоскую) площадку площадью S перпендикулярную к векторам скорости жидкости такую, что скорости частиц жидкости, попадающих на эту площадку, равны по величине. Тогда объем жидкости, протекающий через эту площадку за время dt равен V=vSdt. Если площадка наклонена к потоку, то соответствующий объем равен V=vScosadt, где a - угол между вектором скорости v и единичным вектором нормали к площадке S. Можно записать, что за единицу времени объем протекшей жидкости равен

V=vScos a=() (*), где - так называемый вектор площадки. Если поверхность S не плоская и не бесконечно малая и v не константа, то при вычислении объема протекающей жидкости через поверхность S ее надо разбить на бесконечно малые площадки dS, найти скалярное произведение (*) для каждой бесконечно малой площадки dS и сложить по всей поверхности. Получим:

Выражение типа () или встречаются в самых разнообразных разделах физики и математики. Эти выражения имеют смысл независимо от конкретной природы вектора . Они называются потоком вектора через поверхность S. В общем случае поток вектора через поверхность S обозначается буквой Ф.

Так например, в случае эл. поля величина

(1.27)

называется потоком вектора электрического поля 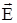через поверхность S (хотя с этим понятием и не связано никакое реальное течение).

Пусть вектор есть геометрическая сумма нескольких полей.

Умножим обе части этого равенства скалярно на справа и проинтегрируем по поверхности S. Получим:

Тогда согласно (1.27) получим, что

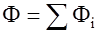(1.28)

где Ф ₁, Ф ₂,...- потоки векторов ₁, ₂,... через ту же поверхность S. Таким образом в то время как векторы складываются геометрически, их потоки через одну и ту же поверхность - алгебраически.

Теорема Гаусса.

Теорема Гауса определяет поток вектора напряженности электрического поля через произвольную замкнутую поверхность.

Пусть электрическое поле создается одним точечным зарядом q. Возьмем произвольную замкнутую поверхность, окружающую этот заряд. В любой точке поверхности S поле определяется выражением:

(1.29)

Рассмотрим простейший случай, когда поверхность - сфера, а заряд q находится в ее центре. Возьмем бесконечно малую площадку сферы площадью dS, для которой можем считать, что вектор одинаков (параллелен) во всех ее точках. Тогда для потока вектора через эту площадку dS можем записать:

Чтобы найти полный поток через поверхность сферы нужно сложить все элементарные потоки, то есть проинтегрировать по всей поверхности:

(1.30)

Результат (1.30) говорит о том, что поток вектора через поверхность сферы с центром в q не зависит от радиуса. Оказывается, что этот результат (1.30) не зависит и от формы замкнутой поверхности, окружающей заряд q (без доказательства). Из (1.28) следует, что (1.30) справедлив и в том случае, когда поверхность S окружает систему зарядов:

В результате получается следующее фундаментальное соотношение:

(1.31)

Это - первое из четырех уравнений Максвелла для электромагнитного поля.

Заметим, что заряды, расположенные во внешнем пространстве по отношению к этой поверхности на величину потока не влияют.

Теорема Гауса для электростатического поля:

Поток Ф_эл вектора напряженности электрического поля через произвольную замкнутую поверхность S равна сумме зарядов, заключенных внутри этой поверхности, с точностью до коэффициента, который в системе СИ равен .

Применения теоремы Гауса.

1). Электростатическое поле бесконечной и равномерно заряженной плоскости.

Возьмем бесконечную плоскость, для которой поверхностная плотность зарядов равна s. Ясно, что вектор напряженности перпендикулярен к этой плоскости в любой точке пространства.

В качестве замкнутой поверхности возьмем цилиндр с площадью основания S₀ и площадью боковой поверхности S. Найдем поток вектора через поверхность этого цилиндра.

?????

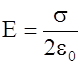(1.32)

2). Поле равномерно заряженного шара.

Возьмем шар радиуса R. Окружим шар сферой с центром в центре шара, радиус которой. В любой точке поверхности сферы вектор направлен по радиусу-вектору . По теореме Гауса поток вектора напряженности равен:

где q - заряд внутри сферы.

(1.33)

(1.33) описывает поле вне равномерно заряженного шара независимо от того заряжен ли он по объему или по поверхности. Таким образом равномерно заряженный шар создает такое поле во внешнем пространстве как если бы весь заряд был сосредоточен в его центре. Это верно для любого сферически симметричного распределения заряда по объему шара. Т.е. поле равномерно заряженного шара во внешнем пространстве такое же, как и у точечного заряда такой же величины,расположенно в центре шара.

Найдем зависимость Е(r) внутри шара, т.е. для r<R.

Возьмем сферу радиуса r.

По теореме Гауса имеем:

(1.34)

где q¢ - заряд внутри сферы.

q¢можно найти, зная объемную плотность заряда r.

, где V- объем сферы.

 

(1.34)

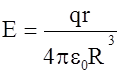(1.35)

Из (1.35) видно, что напряженность внутри равномерно заряженного шара прямо пропорциональна расстоянию от центра.

 

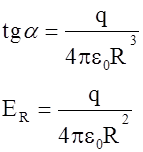
Если заряд равномерно распределен по поверхности сферы, то q `=0. Если 0£r£R и из (1.34) следует, что внутри шара напряженность E=0

 

3). Поле двух параллельных равномерно и разноименно заряженных плоскостей.

Возьмем две параллельные плоскости. Одна плоскость заряжена положительно другая отрицательно. Из рисунка видно, что направление векторов 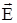обеих плоскостей между ними совпадают, а вне их противоположны. Напряженность поля равномерно заряженной бесконечной плоскости (см. формулу 1.32) равна 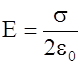. Если плотности зарядов равны, т.е. s₁=s₂=s, то вне плоскостей поле равно нулю, а между ними:

 

(1.36)

Это и есть напряженность поля внутри двух равномерно заряженных плоскостей (поле плоского конденсатора).

 

 

§10. Металлические проводники в электрическом поле.

Проводниками электрического поля называются вещества, имеющие свободные заряды.

Свободным называется заряд, который может перемещаться под действием эл. поля.

К проводникам относят:

1. металлы, в которых свободными являются электроны;

2. водные растворы солей и кислот, в которых свободными являются положительно и отрицательно заряженные ионы;

3. ионизированные газы, в которых свободными являются положительно и отрицательно заряженные ионы, а также - электроны.

Возьмем металлический проводник и поместим его во внешнее электрическое поле. Под действием этого поля внутри металла начнут передвигаться свободные электроны и скапливаться на поверхности (1). На поверхности (2) останутся положительно заряженные ионы. Внутри проводника возникает поле , направленное противоположно . Разделение зарядов будет происходить до тех пор пока = . При этом поле внутри проводника =0. Из этого следует, что силовые линии заканчиваются и начинаются на поверхности проводника и перпендикулярны ей. Если сообщить проводнику заряда q (больший, чем заряд одного электрона), то в силу взаимного отталкивания он весь располагается на поверхности. Модно доказать, что поверхностная плотность заряда обратно пропорциональна радиусу кривизны поверхности проводника:

s_R1>>s_R=¥>>s_-R4

На остриях заряженного проводника как поверхностная плотность зарядов s, так и напряженность эл. поля в пространстве, окружающем острия, принимают максимальные значенияя.

 

§11: Диэлектрики в электростатическом поле. Поляризация диэлектриков. Диэлектрическая проницаемость.

Вещества. которые не проводят электрический ток, называются диэлектриками.

В веществах, которые не относятся к перечисленным в §10, свободных электронов нет и электрический ток через них течь не может. В диэлектриках все электрические заряды сосредоточены или в атомах, или в молекулах, или в ионах.

К диэлектрикам относится большинство твердых веществ (дерево, стекло, фарфор, пластмассы...), чистые жидкости (дистиллированная вода) и неионизированные газы (водород, азот, амиак...). Рассмотрим ряд опытов, связанных с помещением диэлетриков в электрическое поле.

1) Поднесем к заряженному электрометру диэлектрик (не заряженный). При этом показания электрометра уменьшаются.

2) Возьмем диэлектрическую палочку, подвешенную на нити. В электрическом поле диэлектрическая палочка поворачивается, стремясь занять положение вдоль силовых линий поля.

3) Возьмем конденсатор. Поднесем пластину из диэлектрика. Она втягивается внутрь. Это объясняется тем, что вблизи краев пластин в области неоднородного поля вектор имеет составляющую параллельную пластинам. Из этого следует, что на стеклянный брусок действуют силы, втягивающие его внутрь.

Приведенные опыты показывают, что на первоначально не заряженных диэлектриках в электрическом поле возникают электрические заряды. На противоположных поверхностях диэлектрика появляются разноименные заряды (электрические полюсы).

Поэтому это явление называется поляризацией диэлектрика., а заряды, возникающие на диэлектриках при поляризации в электрическом поле называются поляризационнымизарядами.

Явление поляризации сходно с индуктированием проводника, но между обоими явлениями есть важные различия: индукционные заряды можно разделить, а поляризационные - нет!!!

В зависимости от строения веществ возможны два вида поляризуемости:

1) дефформационная (электронная) поляризуемость. Если атом внести в электрическое поле, то электроны атома будут стремиться переместиться против вектора 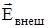, а положительно заряженное ядро – по вектору 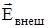. В результате атом деформируется (растягивается вдоль поля).

2) Ориентационная поляризуемость имеет место для не симметричных построений молекул H₂O, NH₃, NaCl. В отсутствие внешнего поля у таких молекул электрический (дипольный) момент . Такие молекулы называются полярными.

При помещении такой молекулы в электрическое поле молекула деформируется за счет деформационного эффекта и поворачивается так, чтобы был параллелен вектору 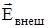. Степень ориентации полярных молекул пропорциональна напряженности электрического поля вектору 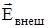. и обратно пропорциональна температуре Т. Т.е. тепловое движение разрушение разрушает ориентацию молекул вдоль поля.

Возьмем конденсатор, внутри которого помещен диэлектрик. Пусть диэлектрик состоит из полярных молекул. В этом случае будет происходить ориентационная поляризуемость.

(1.43)

Величина, показывающая во сколько раз поле внутри однородного диэлектрика меньше поля в вакууме называется диэлектрической проницаемостью вещества и обозначается e.

Соответственно, для сил взаимодействия между зарядами и для напряженностей полей зарядов в однородных диэлектриках в формулах (1.4) и (1.15) в знаменатель входит e.

(1.44)

(1.45)

 

§13: Потенциальная энергия заряженного тела в однородном электростатическом поле.

Пусть имеем однородное эл. поле. На заряд, помещенный в это поле действует сила. Согласно второму закону Ньютона под действием этой силы заряд будет перемещаться. При этом кулоновская сила будет совершать работу. Следовательно можно говорить о том, что в электрическом поле заряд обладает потенциальной энергией, которая при его движении переходит в кинетическую энергию движения. Пусть заряд q из точки 1 переместился в точку 2. Здесь рассмотреть по рис. работу по прямолин. траектории, затем по кривой

1) Работа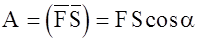

(1.46)

2) Разобьем траекторию на части. Заменим траекторию ступеньками. Видно, что

Итак, работа в однородном электрическом поле не зависит от формы пути. Следовательно, кулоновская сила является консервативной, а электростатическое поле – потенциальным. Тогда выражение 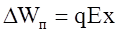имеет смысл потенциальной энергии заряда q в однородном электрическом поле .

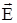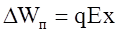(1.47)

Сравните (1.47) с потенциальной энергией тела, поднятого над поверхностью земли: .

Работа (1.46) равна разности потенциальных энергий с противоположным знаком

Если работу совершает эл. поле, то 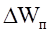<0 и А>0 и наоборот, если заряд перемещается внешней силой против вектора 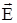, то 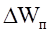>0 и работа кулоновской силы А<0. Как и в механике 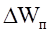определена с точностью до константы. Работа кулоновской силы в однородном поле по замкнутой траектории равна 0.

 

§14: Работа кулоновской силы.

 

!!!Сослаться на механику или воспроизвеси снова

(1.51)

Потенциальная энергия кулоновского поля:

(1.52)

Из (1.52) видно, что если q ₂ и q ₁ одинаковых знаков, то DW >0 и наоборот, при

 

§15: Потенциальность (консервативность) электростатического поля.

 

 

Итак во всех случаях, описываемых выражениями (1.46),(1.50) или (1.55) при любом выборе начальной точки 1 и конечной точки 2 работа А ₁₂ определена только от конечных положений этих точек и не зависит от формы пути.

Силовые поля, удовлетворяющие такому условию, называются консервативными или потенциальными полями.

Соответственно называются и силы, действующие в этих полях.

Покажем, что работа консервативной силы на произвольной замкнутой траектории равна нулю.

Возьмем замкнутую кривую и на ней 2 точки 1 и 2. Работа по переносу заряда между точками 1 и 2 равна: A _1A2 =A _1B2. Если заряд переносить по замкнутому пути 1А2В1, то на участке 2В1 работа

A _2В1 =-A _1B2. тогда A _1A2В1 =A _1А2+ A _2В1 =A _1А2- A _1В2 =A _1А2- A _1A2 =0.

Если перемещаемый заряд q =1, то работа сводится к вычислению криволинейного интеграла

Такой интеграл называется циркуляцией вектора по замкнутому контуру

(1.56)

Можно дать другое определение потенциального поля.

Векторное поле называется потенциальным, если циркуляция вектора по любому замкнутому контуру равна нулю.

Уравнение (1.56) - это второе фундаментальное уравнение электростатики и вместе с уравнением (1.31)

(1.31)

составлет полную систему уравнений, описывающих электростатическое поле в вакууме.

 

§16: Потенциал электростатического поля. Разность потенциалов.

Основываясь на факте существования потенциальной энергии заряда, которой он обладает в электрическом поле, можно ввести еще одну величину, характеризующую свойства поля, совершающего работу по перемещению заряда. Так как потенциальная энергия - DW пропорциональна заряду q, помещенному в поле, то отношение , не зависящее от величины заряда, служит характеристикой поля в точке, в которую помещен этот заряд.

Потенциалом электрического поля называется отношение потенциальной энергии заряда, помещенного в данную точку поля, к величине зтого заряда.

(1.57)

Заметим, что в отличие от напряженности потенциал - величина скалярная. В формуле (1.47) для потенциальной энергии в однородном поле подразумевается, что потенциал j отрицательно заряженной пластины равен нулю (j =0). Выбор точки, в которой потенциал равен нулю, абсолютно произволен, так как практическое значение имеет разность потенциалов. Поэтому величина потенциала выбирается (задается) в точностью до произвольной постоянной и зависит от выбора точки нулевого потенциала.

 

 

Разностью потенциалов j₁ -j₂ (напряжением) между двумя точками 1и 2 называется отношение работы, совершаемой полем при перемещении заряда q из точки 1 в точку 2, к величине этого заряда.

(1.58)

(1.59)

Когда говорят о потенциале в данной точке, то подразумевают, что уже выбрана точка, потенциал которой равен (выбран) нулю (j =0).

Например, для точечного зарядя удобно нулевой потенциал приписать бесконечно удаленной точке. На практике за нулевой потенциал принимают потенциал земли.

Из (1.58) следует, что размерность потенциала j равна [j]==вольт=В

Разность потенциалов между двумя точками равна одному вольту, если при перемещении между этитми точками заряда в 1 Кл совершается работа в 1 Дж.

Пользуясь (1.59) можно установить единицу работы в электрических единицах.

Электрон-вольт – это энергия, которую приобретает частица с зарядом, равным заряду электрона, проходя разность потенциалов в 1 вольт

1эВ=1.6×10^-19 Дж

§17: Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности.

Найдем связь потенциала j с напряженностью электростатического поля Е.

 

 

- единичные векторы вдоль оси координат. Пусть 1 и 2 - бесконечно близкие точки на оси x Расстояние x ₂- x ₁ =dx. Пусть в пространстве задано электрическое поле Е, Е_--Е(x,y,z) работа при перемещении единичного заряда из точки 1 в точку 2 равна dA _x =E _x dx c другой стороны та же работа равна:

dA _x =j ₁- j ₂ =-(j ₂ -j ₁ )=-dj

прировняв, получим: dj=-E_xdx

Аналогично рассуждая для осей y и z получим

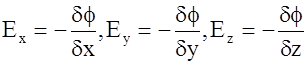(1.60)

Если имеется функция нескольких переменных переменных f(x₁,x₂...), то производные по каждой переменной обозначается - производная функции f по переменной x₁ - j

Формулы (1.60) определяют величины проекции вектора на оси координат. Объединяя (1.60) в одну векторную формулу, получим:

(1.61)

в (1.61) слева, и справа в скобке стоят векторы. Вектор, стоящий в скобках называется градиентом скаляра j и обозначается

(1.62)

Произвольное векторное поле от x,y,z характеризуется тремя скалярными функциями: - проекциями. E_x(x,y,z), E_y(x,y,z), E_z(x,y,z)

Свойство потенциальности накладывает на это векторное поле Е столь сильные ограничение, что для его характеристики достаточно одной скалярной функции - потенциала j (x,y,z).Зная ее (функцию) можно напряженность Е вычислить по формуле

(1.63)

Для вычисления геометрического смысла градиента введем понятие эквипотенциальных поверхностей или поверхностей равного потенциала, т.е. для всех точек эквипотенциальная поверхность потенциал j - постоянен j =const.

 

 

Возьмем на эквипотенциальной поверхности точку О и введем локальную систему координат с началом в этой точке ось z направим по нормали в сторону к возрастанию потенциала j. При этом плоскость (x,y) - касательная к плоскости эквипотенциальной поверхности. Тогда в точке отсчета 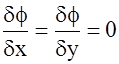. Т.к. , то

, т. е. в точке отсчета потенциал j растет наиболее быстро в направлении нормали , т.е. перпендикулярно поверхности.

Итак grad j от x,y,z- есть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функции j в том же направлении

Вектор направлен противоположно вектору градиента потенциала, т.е. вектор всегда направлен в сторону уменьшения потенциала. Силовые линии являются линиями, вдоль которых потенциал изменяется наиболее быстро. Они таким образом нормальны перпендикулярны поверхности.

Поверхность проводника перпендикулярна к силовым линиям, поэтому эквипотенциал внутри проводника напряженного поля =0, поэтому j =const во всех точках здесь эквипотенциальная поверхность выражена в эквипотенциальный объем. В случае конденсатора имеем

(1.64)

где U-разность потенциалов на...,d-расстояние между ними. Это соотношение используется для определения единицы напряженности. Напряженность равна 1, если в однородном электрическом поле на расстоянии 1 м разность потенциалов равна 1 В.

 

§18: Измерение разности потенциалов.

 

Напряжение измеряется электрометром и электростатическим вольтметром.

§19: Потенциал в простейших электрических полях.

Из (1.57) и (1.53),(1.54) можно для разности потенциалов записать:

(1.65)

Если известно функция Е_е, то есть напряженность поля, то по этой формуле можно вычислить и потенциал j для любой точки

1. Потенциал поля точечного заряда

подставляем в формулу

таким образом вычисляя интеграл получим:

(1.66)

2. потенциал шарового конденсатора

между электродами для a<=r<=b для напряжения имеем

найдем разность потенциалов между внутренней сферой и любой точкой между сферами:

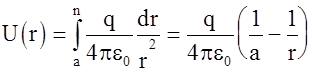
(1.67)

Отсюда разность потенциалов между электродами равна U_ab

Если известна U_ab, т.е. разность потенциалов на пластинах, то выразим U(r) через U_ab

(1.68)

В однородном диэлектрике во всех формулах появляется e.

 

3. Потенциальные системы точечных зарядов.

Для системы точечных зарядов согласно принципу суперпозиций имеем:

(1.69)

U- потенциал результирующего поля в данной точке относительно бесконечности... этой r_i- расстояние от точки до i заряда. N- число зарядов. Аналогично можно рассмотреть потенциал поля протяженно заряженных тел. Сначала находим потенциал создаваемый бесконечно малым элементарным объемом dV, который можно рассматривать как точечный заряд.

, где r - объемная плотность заряда. r - расстояние от рассматриваемой точки поля до dV полный потенциал U равен

(1.70)

где интегрирование (суммирование) идет по всему объему. Если имеем заряженную поверхность

(1.71)

где s(r) - поверхностная плотность заряда, а dS- бесконечно малый элемент поверхности тела.

 

§20: Электроемкость конденсатора.

Если сообщать проводнику разные заряды, то можно заметить во сколько раз изменится заряд, во столько раз изменится и потенциал, т.е. потенциал пропорционален заряду.

(1.12)

С - это коэффициент. Зависит от:

1. размеров и формы проводника.

2. от значения e окружающей Среды (от диэлектрической проницаемости) и ее расположения в пространстве.

С-это емкость проводника.

Аналогично можно определить емкость конденсатора.

 

I. Шаровой конденсатор.

Заряд пластин равен q разности потенциалов.

Þ

Þ (1.73)

Из (1.73) следует, что С зависит от диэлектрика и от радиуса. eсли ,то площадь сферы

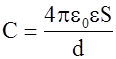(1.74)

II. Емкость плоского конденсатора.

Поле между обкладками почти однородно, краевыми эффектами пренебрегаем. Это можно сделать если d<<S. Пусть s поверхностная плотность заряда положительной пластины, тогда . Напряженность поля между пластинами 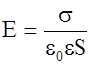и

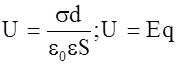
(1.75)

III. Единица электроемкости

Из выражения (1.72) следует, что . Пусть q=1Кл U=1В. Получили единицу емкости.

Фарада - это емкость такого конденсатора, у которого при наличие на каждой обкладке заряда 1Кл между ними возникает разность потенциалов 1В.

IV. Параллельное соединение конденсатора.

Соединим n конденсаторов с емкостями C₁,С₂...С_n параллельно. Если этой системе сообщить заряд, то потенциалы на одноименно заряженных пластинах будут одинаковы

U ₁₁ = U ₁₂ =...= U _1n; U ₂₁ = U ₂₂=...= U _2n, следовательно равны и разности потенциалов U ₁ = U ₂=...= U _n = U. На каждом конденсаторе появляется заряд q₁,q₂...q_n

разделив это равенство на U gjkexbv^

(1.76)

Емкость батареи параллельно соединенных конденсаторов равна сумме их емкостей.

 

V. Последовательное соединение конденсаторов.

При последовательном соединении вследствие электростатической индукции все пластины конденсатора заряжается одинаковыми по величине зарядами. При этом разности потенциалов складываются, т.е. разность потенциалов

(1.77)

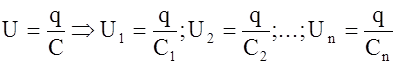
(1.78)

Сравнив (1.78) и (1.76) видим, что параллельное соединение применяется. когда нужно увеличить емкость, последовательное. когда уменьшится или когда большое напряжение надо разделить между искомыми конденсаторами.

 

§21: Энергия электрического поля.

Электрическая энергия и всякая др. энергия зависит только от состояния системы, но не зависит от способа, каким система была приведена в это состояние. Надо найти энергию заряженного конденсатора. То, что обладает энергией видно из следующего опыта. Когда ключ в положении 1 (цепь разомкнута), батарея совершает работу по переносу зарядов электронов с нижней пластины на верхнюю пока разность потенциалов на обкладках не достигнет напряжения батареи U. При перебрасывания ключа в положение 2 лампочка вспыхивает, что говорит о том, что энергия конденсатора, полученная от батареи, и равная работе при переносе зарядов с одной пластины на др., перешла в тепловую и световую энергию. Если конденсатор на заряжен. то на каждой из его обкладок имеется смесь, равных количеств положительных и отрицательных электричеств. Будем переносить положительный заряд малыми порциями с верхней обкладки на нижнюю. При этом внешней силой совершается работа против сил электрического поля. dA=Udq, где U - мгновенное значение разности потенциалов между обкладками; q - заряд на пластинах в этот момент времени.

Эта работа идет на повышение энергии W конденсатора, т.е.

(1.79)

Полную работу найдем интегрируя (1.79). Чтобы не прибегать к таблице интегралов заметим, что справа в (1.79) стоит выражение похожее на работу силы упругости kx•Dx т.е. функции под знаком интеграла такая: - зависит от q т.е. эта энергия равна площади под прямой

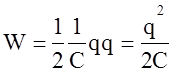(1.80)

(1.80) определяет энергию конденсатора, имеющего заряд q на пластинах. Используя зависимость q=CU. (1.80) можно написать в разных видах:

(1.80’)

Теперь можно поставить вопрос: где именно сосредоточена (локализована) электроэнергия? Можно допустить, то она сосредоточена либо на обкладках, либо в электрическом поле конденсатора. Ответ на этот вопрос может дать только опыт. При рассмотрении const электрических полей. Четкого ответа из опыта получить нельзя т.к. в этом случае мы всегда имеем заряды окруженные полем и наоборот. Ответ получим переменные электрического поля и соотношения или магнитные волны, которые можно получить без электрических зарядов и!!!!

Отсюда следует что энергия замкнутой энергии заключена в электрическом поле. Тогда преобразуем (1.80) так, чтобы выражение для энергии э

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: