Одноместные и двухместные двоичные функции.

Т.к количество различных двоичных функций ограничено, то все они могут быть перечислены.

Например, одноместных двоичные функций (от одного аргумента) всего 4,

- две из которых константы (0) и (3)- при любом значении аргумента х выдают значения соответственно 0 и 1;

- функция (1) повторяет значения аргумента

- а функция (2) изменяет значения аргумента на «противоположное.»

Таблица 2

 

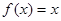
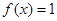
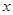
	(0)	(1)	(2)	(3)

 

Последняя из названных функций 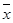называется отрицанием и часто обозначается

Аналогично могут быть перечислены и все двухместные двоичные функции

Таблица 3

 

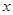
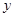
		(0)	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)

К числу основных двоичных функций относятся:

- конъюнкция (1);

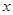
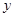
Конъюнкция (или логическое произведение) равно 1 тогда и только тогда, когда оба операнда (логических сомножителя) равны 1.

- дизъюнкция 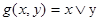(7);

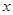
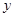
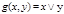
Дизъюнкция (или логическая сумма) равно 0 тогда и только тогда, когда оба операнда (логических слагаемых) равны 0.

- импликация 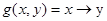(13);

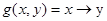
Импликация (или логическое следствие) равно 1, если первый операнд меньше либо равен второму (считается, что двоичные 0<1).

 

- эквива­лентность (9);

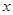
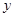
Эквива­лентность равна 1, если операнды совпадают

- сумма по модулю 2 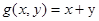(6);

 

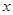
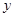
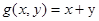
- штрих Шеффера 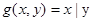(14);

 

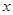
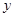
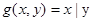
- стрелка Пирса. 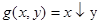(8)

 

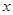
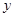
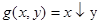
Алгебра двоичных функций.

Название «логических» двоичные функции заслужили в связи с тем, что механизмы их преобразований отражают формальную логику человеческого мышления. Так, если предположить, что переменным двоичных функций (принимающим всего два значения) соответствуют утверждения, про которые можно оказать одно из двух: "это истина" или "это ложь", то на их основе с примением двоичных функций, выполняющим роль логических операций, можно построить более сложные утверждения.

Например,

- "утверждение Х" И "утверждение У" образуется операцией

- "утверждение Х" ИЛИ "утверждение У" образуется операцией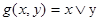

- "утверждение Х" ЭКВИВАЛЕНТНО "утверждению У" образуется операцией

- ИЗ "утверждения Х" СЛЕДУЕТ "утверждение У" образуется операцией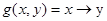

- "НЕ утверждение Х" образуется операцией ;

Двухместные и одноместные функции (операции) образуют Алгебру логических функций, что означает достаточность их совокупности для представления любой логической функции. Т.е. любая логическая функция от конечного числа логических переменных может быть представлена с помощью двухместных и одноместных функций в виде некоторого выражения и наоборот, любому правильно построенному из логических переменных и операций выражению будет отвечать некоторая логическая функция. При этом предполагается, что в правильно записанном выражении

1. операнды двухместных операций записываются слева и справа от знака операции,

2. операции выполняются таким образом, что

- первым производится – отрицание

- вторым – логическое произведение

- третьим – логическая сумма и все остальные операции в очередности их записи

3. очередность пункта 2 может быть изменена с помощью расстановки скобок причем количество открывающих скобок равно количеству закрывающих и скобки раскрываются в обычном порядке «от внутренних к наружным»

Пример 1. Построить таблицу истинности следующей двоичной функции.

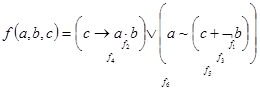
р

 

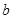
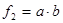
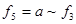
Алгебру логических функций характеризуют законы

идемпотентности

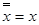двойного отрицания

коммутатитвности

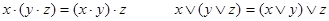ассоциативности

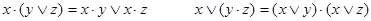дистрибутивности

де-Моргана (инверсии)

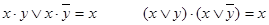склеиванияи

поглощения

Совокупность приведенных законов легко может быть расширена новыми тождествами.

Две функции алгебры логики (ФАЛ) являются эквивалентными или тождественно равными, если равны их значения на соответствующих наборах. Например, нетрудно заметить, что

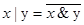
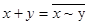
и т.д.

Приведенные тождества указывают на избыточность системы логических функций. В самом деле, ниже будет показано, что любая логическая функция может быть представлена с помощью набора из 3-х, 2-х или даже одной функции, обладающего свойствами базиса.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: