 |
Совершенная дизъюнктивная нормальная форма.
|
|
|
|
Любую функцию алгебры логики можно представить в виде (СДНФ). СДНФ представляет двоичную функцию в виде логической суммы (дизъюнкии) нескольких. логических произведений (конъюнкций), каждое из которых включает в себя все логические переменные функции, взятые с отрицанием или без.
В СДНФ
· нет двух одинаковых слагаемых;
· ни одно слагаемое не содержит двух одинаковых множителей;
· ни одно слагаемое не содержит переменной вместе с ее отрицанием;
· в каждом слагаемом в произведение увязана либо сама переменная, либо еэ отрицание.
Алгоритм построения СДНФ
1. Отметить в таблице истинности функции все наборы, на которых функция равна 1
2. По каждому из отмеченных наборов построить логическое произведение (конъюнкцию) из всех переменных, где переменная
Þ входит без знака отрицания, если в наборе ей соответствует 1
Þ входит со знаком отрицания, если в наборе ей соответствует 0
3. Все построенные логические произведения объединяются в логическую сумму (дизъюнкцию)
Если обозначить  , где
, где  - переменная,
- переменная,  - значение этой
- значение этой
переменной на  -м наборе, то СДНФ формально можно записать в виде выражения
-м наборе, то СДНФ формально можно записать в виде выражения
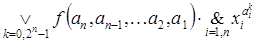
Пример 2. Построить СДНФ ф у нкции из примера 1.
Анализируемая функция равна 1 на наборах 0, 1, 2, 4, 6, 7

Совершенная конъюнктивная нормальная форма.
Любую логическую функцию можно представить в виде совершенной конъюнктивной нормальной формы (СКНФ). СКНФ представляет двоичную функцию в виде логического произведения (конъюнкии) нескольких. Заключенных в скобки логических сумм (дизъюнкций), каждая из которых включает в себя все логические переменные функции, взятые с отрицанием или без
В СКНФ
· нет двух одинаковых сомножителей;
|
|
|
· ни один из сомножителей не содержит двух одинаковых слагаемых;
· ни один из сомнокителей не содержит переменной и ее отрицание;
· в каждом из сомножителей содержится либо сама переменная, либо ее отрицание.
Алгоритм построения СКНФ
1. Отметить в таблице истинности функции все наборы, на которых функция равна 0
- По каждому из отмеченных наборов построить логическую сумму (дизъюнкцию) из всех переменных, где переменная
Þ входит без знака отрицания, если в наборе ей соответствует 0
Þ входит со знаком отрицания, если в наборе ей соответствует 1
- Все построенные логические суммы заключаются в скобки и объединяются в логическое произведение (конъюнкцию)
СКНФ формально можно записать в виде выражения

Пример 3. Построить СКНФ ф у нкции из примера 1.
Анализируемая функция равна 0 на наборах 3, 5

Базисы функций алгебры логики
Базисом функций алгебры логики называется такой набор функций, с помощью которого можно выразить любую функцию двоичную функцию. Например, таким свойством обладает набор функций
А)  - называемый избыточным базисом.
- называемый избыточным базисом.
Факт того, что набор функций  является базисным подтверждается возможностью представления произвольной функции в виде СДНФ или СКНФ.
является базисным подтверждается возможностью представления произвольной функции в виде СДНФ или СКНФ.
Если набор функций (А) базисный, то (по закону де-Моргана) базисными являются также наборы (Б) и (В) |
Б)  , т.к.
, т.к. 

В)  , т.к.
, т.к. 
Если набор функций (Б) базисный, то базисным является также набор (Г)
Г)  , т.к.
, т.к. 
Если набор функций (В) базисный, то базисным является также набор (Д)
Д)  , т.к.
, т.к. 
Если набор функций (Г) базисный, то базисным является также набор (Е)
Е) |, т.к. 
Если набор функций (Д) базисный, то базисным является также набор (Ж)
Ж) 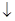 , т.к.
, т.к. 
Пример 4
. Построить представление ф у нкции импликации  во всевозможных базисах.
во всевозможных базисах.
В избыточном базисе (А)  в виде СДНФ, либо
в виде СДНФ, либо  в виде СКНФ.
в виде СКНФ.
Для получения функции в базисе (Б) надо избавиться от операций дизъюнкции. Приэтом естественно исходить из представления, где употребление этой операции ниже, т.е. использовать СДНФ функции).
|
|
|

Для получения функции в базисе (В) надо избавиться от операций конъюнкции,. используяь СКНФ).

Исходя из вида функции в базисе (Б), получим ее вид в базисах (Г) и (Е)

А исходя из вида функции в базисе (В), получим ее вид в базисах (Д) и (Ж) |

Полином Жегалкина.
Любую логическую функцию можно представить в виде полинома. Произведение, логических переменных называется монотонным, если оно содержит переменные без отрицаний. Сумма по модулю 2 попарно различных монотонных произведении называется полиномом Жегалкина (ПЖ):
Алгоритм построения полинома Жегалкина
Для произвольной логической функции от n - переменных:
1. записать в общем виде полином Жегалкина с неопределенными коэффициентами;
Например, для функции 2-х переменных общий вид полинома

2. решить систему.из 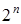 линейных уравнений относительно неизвестных коэффициентов, образуемую путем подстановки значений функции на
линейных уравнений относительно неизвестных коэффициентов, образуемую путем подстановки значений функции на 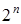 наборах таблицы истинности;
наборах таблицы истинности;
- полученные значения коэффициентов подставить в полином.
Пример 5. Построить полином Жегалкина для функции из примера 1.
Общий вид полинома от 3-х переменных
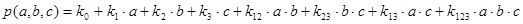

| 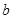
| 
| 
| 
| 
|
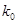
| 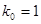
| ||||
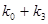
| 
| ||||

| 
| ||||

| 
| ||||

| 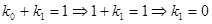
| ||||

| 
| ||||

| 
| ||||

| 
|
Таким образом ПЖ 
Заметим, что возможность представления любой функции в виде полинома Жегалкина указывает на базисность набора функций  - «базис Жегалкина».
- «базис Жегалкина».
|
|
|


