 |
Примеры построения таблиц значений и графиков функций
|
|
|
|
Лабораторная работа
Табулирование функций и построение графиков
Цель работы:
- изучить операцию заполнения ячеек данными;
- изучить операцию копирования формул с помощью заполнения;
- научиться решать расчетные задачи табулирования функции одной переменной для шагового аргумента;
- рассмотреть вопросы вычисления таблиц функций, заданных различными аналитическими выражениями, функций, зависящих от параметра, функций заданных в параметрической форме или в полярной системе координат.
Приемы копирования и заполнения ячеек
Абсолютные, относительные, смешанные ссылки
Напомним, что ссылка вида A1 называется относительной. Относительная ссылка меняется при копировании формулы из одной ячейки в другую, так что сохраняется относительное расположение влияющих на формулу ячеек и ячейки, содержащей формулу. Это позволяет создать расчетные таблицы, содержащие повторяющиеся вычисления для данных, находящихся в различных ячейках.
Пример. В ячейку C3 введена формула =(A2+A3+A4)/3. При ее копировании в ячейку С4 получим формулу =(A3+A4+A5)/3. При копировании в ячейку F10 получим формулу =(D9+D10+D11)/3.
Просмотреть зависимые и влияющие ячейки можно с помощью панели Зависимости. Она вызывается по команде Вид|Панели инструментов|Настройка, вкладка Панели инструментов, установить флажок Зависимости. Затем выделяется ячейка с формулой. При нажатии кнопки Влияющие ячейки появляются стрелки от влияющих ячеек к зависимым. Кнопка Зависимые ячейки показывает, на какие ячейки с формулами влияет данная ячейка. Для снятия стрелок используется кнопка Убрать все стрелки.
Ссылка вида $A$1 называется абсолютной. При копировании формул абсолютные ссылки не меняются. Это позволяет использовать константы в повторяющихся вычислениях. Ссылка вида $A1 называется смешанной. При копировании формулы со ссылкой данного типа не меняется заголовок столбца, а номер строки может меняться. Наоборот, при использовании другой смешанной ссылки типа A$1 не меняется номер строки, а заголовок столбца может меняться.
|
|
|
Заполнение ячеек
Заполнение ячеек - это перенос данных из одной ячейки в ряд смежных ячеек строки или столбца с возможностью их изменения по некоторому закону. Операция выполняется по команде Правка|Заполнить…. В диалоговом окне команды можно указать различные варианты заполнения.
· Вычисление значений аргумента по типу арифметической или геометрической прогрессии. Порядок работы следующий: ввести первое значение в требуемую ячейку и выделить эту ячейку, вызвать команду Правка|Заполнить|Прогрессия. В ее диалоговом окне установить расположение данных (строки, столбцы), тип прогрессии, шаг изменения аргумента, предельное значение аргумента. После подтверждения команды (OK) столбец (или строка) будет заполнен. в направлении увеличения адресов.
· Заполнение ячеек заголовками строк или столбцов вида Урок 1, Урок 2, и т.д. выполняется так: вводится первый заголовок, выделяется заполняемый диапазон ячеек и выполняется команда Правка|Заполнить|Прогрессия. В диалоговом окне команды выбирается Автозаполнение.
· Возможно заполнение последовательных ячеек датами с заданным интервалом, названиями месяцев, дней недели, годов, часов. Предлагаем эту операцию освоить самостоятельно экспериментальным путем с помощью все той же команды Правка|Заполнить |Прогрессия.
· Заполнение ячеек формулами разберем на примере построения таблицы значений функции. Предварительно отметим следующее: при копировании формул из одних ячеек в другие, обычные (так называемые относительные) ссылки на ячейки изменяются с сохранением структуры зависимости от исходных данных. Например, введем в ячейку B1 формулу =A1+5. При копировании формулы в нижележащую ячейку B2 она превращается в формулу =A2+5. Заполнение ячеек формулами есть не что иное, как копирование формул в последовательные ячейки таблицы. Оно выполняется следующим образом: формула вводится в первую ячейку ряда, затем нужно выделить диапазон для ввода формул и применить команду Правка|Заполнить| Вниз (или Вправо).
|
|
|
Замечание. Если ссылка на ячейку в формуле является абсолютной ($A$10), то при копировании формулы она не меняется. Например, формула =$A$10+A1 при копировании изменит ссылку лишь на ячейку A1.
Добавление. Можно быстрее выполнять команду заполнения с помощью Маркера заполнения. Данные типа арифметической прогрессии вводятся в две первые ячейки заполняемого ряда. Затем, выделив эти ячейки, нужно установить указатель мыши на Маркер заполнения - маленький черный квадрат в правом нижнем углу выделенного диапазона и протащить указатель вдоль заполняемого столбца до появления последнего значения. При отпускании мыши ряд будет заполнен данными. Заполнение ячеек формулой выполняется аналогично, но только еще проще - достаточно протащить формулу за маркер заполнения вдоль требуемого ряда.
Примеры построения таблиц значений и графиков функций
Пример 1. (Функция одной переменной для шагового аргумента). Построить таблицу значений функции  для аргумента x, изменяющегося от 0 до 1,5 с шагом 0,1. Построить график функции.
для аргумента x, изменяющегося от 0 до 1,5 с шагом 0,1. Построить график функции.
Решение. Решение разбивается на два основных этапа: построение таблицы значений функции и построение графика функции.
Построение таблицы
· Наберем заголовки столбцов для x и y в ячейках A1, B1.
· Наберем первое значение x, равное 0, в ячейку A2.
· Выполним команду Правка|Заполнить|Прогрессия, зададим в диалоге Расположение в столбце, Арифметическая прогрессия, Шаг 0,1, Предельное значение 2. Заполнятся ячейки A4:A22.
· В ячейку B2 введем формулу: =SIN(4*A2)^2/(A2+1) и скопируем ее в ячейки B3:B22
· Выполним форматирование данных (чисел) и обрамление таблицы. Фрагмент рабочего листа с таблицей показан на рис.5.1.
|
|
|
 |
Построение графика функции. Для построения графика выделим диапазон данных (ячейки A1:B22) и построим точечную диаграмму, вид которой представлен на рис. 5.2.
|
 |
Пример 2. (Функция, заданная различными аналитическими выражениями (сложная функция)). Построить таблицу значений и график функции

для аргумента x, изменяющегося от -2 до 2 с шагом 0,2
Решение
Построение таблицы. Решение выполним в том же файле, что и предыдущий пример, но на новом листе Excel. Последовательность заполнения ячеек аналогична примеру 1.
В ячейку B2 введем формулу:
=ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2))
и скопируем ее в нижележащие ячейки для всех значений x.
 |
|
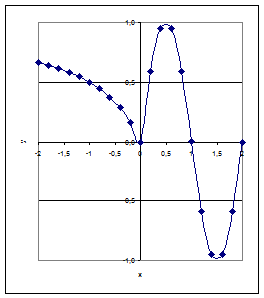 |
Построение графика функции также полностью аналогично построению предыдущего примера, если заданная функция непрерывна.
Замечание. Если функция терпит разрыв при переходе от одного аналитического выражения к другому, то нужно построить на одной диаграмме два графика, каждый из которых отвечает области непрерывности функции. В случае разрывной функции можно строить один график, если выбрать вид графика из отдельных точек
Пример 3. (Функция, зависящая от параметра). Построить таблицу значений и график функции  для аргумента x, изменяющегося от -1 до 3 с шагом 0,2 при заданных значениях a и b.
для аргумента x, изменяющегося от -1 до 3 с шагом 0,2 при заданных значениях a и b.
Решение
· Введем заголовки столбцов для x и y в ячейки A1, B1 и значения a, b в отдельные ячейки D1, F1.
· Заполним столбец A2:A22 значениями x.
· Введем формулу для y в ячейку B2
=EXP($D$1*A2)*COS($F$1*A2) и скопируем ее в ячейки B3:B22.
·
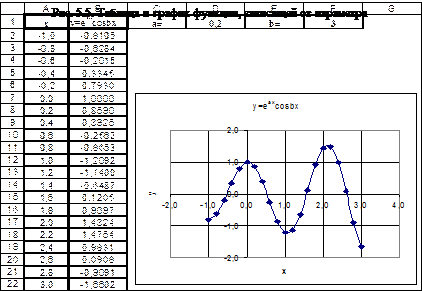 |
Построим график аналогично примеру 1 (см. рис.5.5)
Замечание. Меняя значения параметров, можно получить совершенно другое поведение функции. Рекомендуется проанализировать поведение функции при a> 0 и a<0, а также рассмотреть уменьшение и увеличение b.
Пример 4. (Функция, заданная параметрическими уравнениями). Вычислить таблицу значений функции, заданной параметрическими уравнениями и построить ее график. В качестве примера рассмотрим построение окружности.
|
|
|
Параметрические уравнения окружности рассмотрим для значений параметра, пробегающих полный оборот вокруг начала координат:
 (1)
(1)
|
|
|


