 |
Построение таблицы значений функции
|
|
|
|
· Перейдем на новый рабочий лист.
· Зададим заголовки столбцов t, x, y.
· Заполним первый столбец значениями t, применив еще один способ задания аргумента: каждое последующее значение вычислим через предыдущее, добавляя шаг. В ячейке D2 вычислим 
по формуле =ПИ()/16. В ячейку A2 введем 0, в ячейку A3 введем формулу =A2+$D$2, которую копируем вниз до значения 2p.
· Введем в ячейку B2 формулу =COS(A2); в ячейку C2 формулу =SIN(A2)
· Выделим ячейки B2, C2 и копируем их для всех значений t с помощью заполнения.
· Форматируем таблицу по образцу.
Построение графика функции
· Выделим диапазон B1:C22
· Вызовем Мастер диаграмм и построим точечную диаграмму. В процессе построения зададим заголовки диаграммы и осей, уберем легенду, назначим линии сетки.
· Затем отредактируем диаграмму: по команде Ф ормат оси зададим точность – один знак после запятой, по команде Формат области построения укажем рамку Невидимая.
· Выполним растяжение-сжатие диаграммы, так чтобы получилась окружность, а не эллипс.
Результат построения показан на рис. 5.7.
|
 |
Замечания
1. Несколько изменив уравнения (1) можем получить и параметрические уравнения эллипса. Как работать с функциями, содержащими постоянные параметры, было рассмотрено в предыдущем примере. Итак, эллипс с осями a, b задается уравнениями:
где a, b - положительные константы
2. В примерах 1-3 были рассмотрены функции, заданные аналитически в явном виде, т.е. формулой, в которой зависимая переменная y вычислялась через независимую переменную x. Существует другой способ задания функции, в котором обе этих величины являются функциями одного и того же параметра t. Тогда каждому значению t соответствует пара значений (x, y), определяемых формулой
|
|
|
(2)
Предположим, что по каждому значению x=f(t) можно найти единственное значение t, которому в свою очередь можно сопоставить y=g(t). Тогда можно считать y функцией x. Такой способ задания функции называется параметрическим. Если рассматривать множество пар (x,y), определяемых уравнением (2) как множество точек на плоскости, то уже нет необходимости требовать единственности решения t по x. И в этом случае считаем, что задана функция y от x параметрическими уравнениями (2). Может оказаться, что одному значению x соответствует два или даже несколько значений y. В ряде случаев простые параметрические уравнения позволяют задать функции, для которых явные уравнения очень сложны или не существуют.
3. Функция, заданная в полярной системе координат, легко преобразуется к параметрической форме. Действительно, декартовы координаты x, y связаны с полярными координатами r, j уравнениями
(3)
Если задано уравнение кривой в полярной системе координат 
, то подставив это выражение в уравнения (3), получим параметрические уравнения кривой с полярным углом j в качестве параметра.
Отчет к лабораторной работе
Отчет оформляется в виде документа Word и содержит решение варианта с описанием, аналогичным рассмотренным примерам.
Варианты заданий
Задача 1. Вычислить таблицу значений функции для аргумента, изменяющегося с данным шагом в заданном интервале, и построить ее график
| Таблица 5.1 | |||
| Вариант | Функция | Интервал изменения аргумента | Шаг изменения аргумента |
| [0, 10] | 0,5 | |
| [-1,4] | 0,25 | |
| [-2,2] | 0,2 | |
| [-4,4] | 0,5 | |
| [-2,2] | 0,2 | |
| [0,5] | 0,25 | |
| [0,4] | 0,2 | |
| [-4,2] | 0,25 | |
| [1,10] | 0,5 | |
| [-10,10] | ||
| [-2,3] | 0,2 | |
| [-3,3] | 0,25 | |
| [-3,3] | 0,25 | |
| [-10,10] | ||
| [-5,5] | 0,5 |
Задача №2.
|
|
|
Построить график функции. Значения аргумента задать таким образом, чтобы получить на графике не менее 15 точек. Для автоматизации вычислений использовать функцию ЕСЛИ.
.
, y=0,4
, a=1,2
, y=4
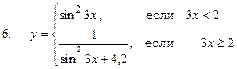
, y=2
Задача 3. Вычислить таблицу значений функции, заданной параметрическими уравнениями или уравнением в полярной системе координат, и построить ее график. В случае задания функции в полярной системе координат перейти к параметрическим уравнениям. Константы, входящие в уравнения, являются положительными и, если не задано их конкретное значение, могут быть взяты равными единице.
Таблица 5.2
| № | Название кривой | Уравнения кривой |
| Циклоида | 
| |
| Астроида | 
| |
| Двухлепестковая роза | 
| |
| Кардиоида | 
| |
| Конхоида | 
| |
| Улитка | 
| |
| Гипербола | 
| |
| Четырехлепестковая роза | 
| |
| Спираль | 
| |
| Архимедова спираль | 
|
|
|
|
