 |
Обработка результатов наблюдений
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Технологический институт
Федерального государственного образовательного учреждения
Высшего профессионального образования
"Южный федеральный университет"
Приоритетный национальный проект "образование"
Кафедра автоматизированных систем научных исследований и экспериментов
Сборник методических указаний
К выполнению лабораторных работ
По курсу
Метрология, стандартизация, сертификация
Для студентов специальностей
200503 Стандартизация и сертификация
210100 Электроника и наноэлектроника
211000 Конструирование и технология электронных средств;
200100 Приборостроение
222900 Нанотехнологии и микросистемная техника
201000 Биотехнические системы и технологии
| Таганрог 2011 |
УДК
Составитель Т.В.Шушкевич.
Сборник методических указаний к выполнению лабораторных работ по курсу "Метрология, стандартизация, сертификация". – Таганрог: Изд-во ТТИ ЮФУ, 2011. – ___ с.
Данное пособие содержит основные теоретические сведения, методики выполнения лабораторных работ и описание используемых приборов.
Табл.__. Ил. ___. Библиогр.: ___ назв.
Рецензент С.В.Кавчук, канд. техн. наук, доцент кафедры
АСНИ и Э ТТИ ЮФУ.
 | |||
 |
1. Стандартная обработка результатов прямых измерений с многократными наблюдениями
Цель работы: ознакомление с методикой выполнения прямых измерений с многократными наблюдениями. Получение навыков стандартной обработки результатов наблюдений, оценивания погрешностей и представления результатов измерений.
|
|
|
Общие сведения
В данной лабораторной работе необходимо провести измерение сопротивления n резисторов с помощью цифрового измерителя иммитанса
Е7-21, а затем обработать полученные результаты. Обработка результатов измерений ведется по ГОСТ 8.207-76 "ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения". Этот ГОСТ регламентирует методику выполнения прямых измерений с многократными независимыми наблюдениями и устанавливает основные положения методов обработки результатов наблюдений и оценивания погрешностей результатов измерений.
При выполнении лабораторной работы следует иметь в виду, что значение сопротивления каждого резистора несколько отличается от номинального. Для каждого конкретного резистора отклонение от номинала – детерминированная (постоянная) величина; а для совокупности резисторов данного типа и номинала – случайная величина, меняющаяся от экземпляра к экземпляру. Анализ этой величины может использоваться, в частности, для определения качества и управляемости процесса производства.
Обработка результатов наблюдений
При статистической обработке группы результатов наблюдений 
следует выполнить следующие операции.
1. Исключить известные систематические погрешности из результатов наблюдений.
2. Вычислить среднее арифметическое исправленных результатов наблюдений 
, принимаемое за результат измерения:
.
3. Вычислить оценку среднего квадратического отклонения (СКО) результата наблюдения
.
Вычислив оценку СКО результата наблюдений, необходимо проверить наличие в группе наблюдений грубых погрешностей (промахов). При числе измерений n >20,…,50 можно применить критерий 3 σ: при нормальном законе распределения ни одна случайная погрешность 
с вероятностью 0.997 не может выйти за пределы ±3 σ. Наблюдения, содержащие грубые погрешности (т.е. те, для которых выполняется условие 
) исключают из группы и заново повторяют вычисления и S(x).
|
|
|
Если n < 20, применяют критерий Романовского. При этом вычисляют отношение
и полученные значения 
сравнивают с теоретическим 
при выбранном уровне значимости α по таблице 1.1.
Таблица 1.1
| α | Число измерений | ||||||
| n =4 | n =6 | n =8 | n =10 | n =12 | n =15 | n =20 | |
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,64 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
Если 
, то результат отбрасывают.
4. Вычислить оценку среднего квадратического отклонения результата измерения
.
5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.
При числе результатов наблюдений n > 50 для проверки принадлежности их к нормальному распределению предпочтительным является один из критериев: 
Пирсона или ω2 Мизеса-Смирнова.
При числе результатов наблюдений 
принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по излагаемой методике возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.
При числе результатов наблюдений 15< n <50 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий, приведенный ниже. В случае, если хотя бы один из критериев не соблюдается, считают, что распределение результатов наблюдений группы не соответствует нормальному.
Критерий 1. Вычисляют отношение 
,
где 
– среднее отклонение результатов наблюдений, определяемое по формуле
;
S* – смещенная оценка среднего квадратического отклонения, вычисляемая по формуле
.
Если найденное 
удовлетворяет неравенству
,
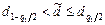где 
и 
– квантили распределения (табл. 1.2);
– заранее выбранный уровень значимости критерия,
переходят к проверке второго критерия. Если неравенство не выполняется, считают, что результаты наблюдений не принадлежат нормальному закону и второй критерий не проверяют.
Таблица 1.2
|
|
|
| n |
|
| ||
| 0,01 | 0,05 | 0,95 | 0,99 | |
| 0,9137 | 0,8884 | 0,7236 | 0,6829 | |
| 0,9001 | 0,8768 | 0,7304 | 0,6950 | |
| 0,8901 | 0,8686 | 0,7360 | 0,7040 | |
| 0,8826 | 0,8625 | 0,7404 | 0,7110 | |
| 0,8769 | 0,8578 | 0,7440 | 0,7167 | |
| 0,8722 | 0,8540 | 0,7470 | 0,7216 | |
| 0,8682 | 0,8508 | 0,7496 | 0,7256 | |
| 0,8648 | 0,8481 | 0,7518 | 0,7291 |
Критерий 2. Оценка по критерию 2 заключается в определении числа отклонений 
экспериментальных значений 
превосходящих теоретическое значение 
для заданного уровня значимости 
. Для этого при заданных и n находятся параметры α и 
по данным из таблицы 1.3.
Таблица 1.3
| n |
| Значения α при уровне значимости q2 | ||
| 0,01 | 0,02 | 0,05 | ||
| 0,98 | 0,98 | 0,96 | ||
| 11-14 | 0,99 | 0,98 | 0,97 | |
| 15-20 | 0,99 | 0,99 | 0,98 | |
| 21-22 | 0,98 | 0,97 | 0,96 | |
| 0,98 | 0,98 | 0,96 | ||
| 24-27 | 0,98 | 0,98 | 0,97 | |
| 28-32 | 0,99 | 0,98 | 0,97 | |
| 33-35 | 0,99 | 0,98 | 0,98 | |
| 36-49 | 0,99 | 0,99 | 0,98 |
Далее находится квантиль интегральной функции нормированного нормального распределения , которая определяется из таблицы 1.4 для значения 
.
Таблица 1.4
| F(t) | t | F(t) | t | F(t) | t |
| 0,0005 | -3,2905 | 0,30 | -0,5244 | 0,80 | +0,8416 |
| 0,005 | -2,5750 | 0,35 | -0,3853 | 0,85 | +1,0364 |
| 0,01 | -2,3267 | 0,40 | -0,2533 | 0,90 | +1,2816 |
| 0,015 | -2,1711 | 0,45 | -0,1257 | 0,95 | +1,6449 |
| 0,02 | -2,0541 | 0,50 | 0,0000 | 0,98 | +2,0541 |
| 0,05 | -1,6449 | 0,55 | +0,1257 | 0,985 | +2,1711 |
| 0,10 | -1,2816 | 0,60 | +0,2533 | 0,99 | +2,3267 |
| 0,15 | -1,0364 | 0,65 | +0,3853 | 0,995 | +2,5750 |
| 0,20 | -0,8416 | 0,70 | +0,5244 | 0,9995 | +3,2905 |
| 0,25 | -0,6745 | 0,75 | +0,6745 |
Затем вычисляются экспериментальные значения параметра по формуле 
.
Вычисленное значение сравнивается с теоретическим значением и подсчитывается число отклонений , для которых удовлетворяется неравенство 
. Значение 
сравнивается с теоретическим числом отклонений 
. Если 
, то распределение данного ряда наблюдений не противоречит нормальному.
В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q1, а для критерия 2 – q2, то результирующий уровень значимости составного критерия
q ≤ q1 + q2.
6. Вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения.
Доверительные границы случайной погрешности результата измерения в соответствии с ГОСТ 8.207-76 устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
|
|
|
Доверительные границы ε (без учета знака) случайной погрешности результата измерения находят по формуле
,
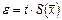где t – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по табл.1.5.
Таблица 1.5
| n –1 | P = 0.95 | P = 0.99 | n –1 | P = 0.95 | P = 0.99 |
| 3,182 | 5,841 | 2,120 | 2,921 | ||
| 2,776 | 4,604 | 2,101 | 2,878 | ||
| 2,571 | 4,032 | 2,086 | 2,845 | ||
| 2,447 | 3,707 | 2,074 | 2,819 | ||
| 2,365 | 3,499 | 2,064 | 2,797 | ||
| 2,306 | 3,355 | 2,056 | 2,779 | ||
| 2,262 | 3,250 | 2,048 | 2,763 | ||
| 2,228 | 3,169 | 2,043 | 2,750 | ||
| 2,179 | 3,055 | ∞ | 1,960 | 2,576 | |
| 2,145 | 2,977 |
7. Вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения.
Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности:
– метода;
– средств измерений;
– вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.
При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерении каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их принимают за равномерные.
Границы неисключенной систематической погрешности θ результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле
,
где θi – граница i -й неисключенной систематической погрешности;
k – коэффициент, определяемый принятой доверительной вероятностью.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
Коэффициент k принимают равным 1,1 при доверительной вероятности
Р = 0,95.
При доверительной вероятности Р = 0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m > 4). Если же число суммируемых погрешностей равно четырем или менее четырех (m ≤ 4), то коэффициент k определяют по графику зависимости, приведенному на рис. 1.1.
|
|
|
Коэффициент k зависит от двух величин: m и l.
m – число суммируемых погрешностей. Для кривой 1 m = 2, для кривой 2 m = 3, для кривой 3 m = 4.
.
При трех или четырех слагаемых в качестве θ1, принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве θ2 следует принимать ближайшую к θ1 составляющую.
8. Вычислить доверительные границы погрешности результата измерения.
Для определения доверительных границ погрешности результата измерения доверительную вероятность Р принимают равной 0,95.
В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99.
В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р = 0,99 принимать более высокую доверительную вероятность.
Для определения доверительных границ погрешности результата измерения вычисляют отношение 
.
Если 
, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата Δ = ±ε.
Если 
, то случайной погрешностью можно пренебречь и принять границы погрешности результата Δ = ±θ.
Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15 %.
Если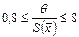 
, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины.
Границы погрешности результата измерения в этом случае вычисляют по формуле
Δ = ±KSΣ.
где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
SΣ – оценка суммарного среднего квадратического отклонения результата измерения.
Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле
.
Коэффициент К вычисляют по эмпирической формуле
.
9. Оформить результат измерения по МИ 1317–86.
При симметричной доверительной погрешности результаты измерений представляют в форме
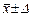, Р.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δ. Число значащих цифр в значении погрешности не должно превышать двух.
При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей результаты измерений представляют в форме
.
В случае, если границы неисключенной систематической погрешности вычислены путем построения композиции, следует дополнительно указывать доверительную вероятность Р.
|
|
|
