 |
Свойства кривых второго порядка
|
|
|
|
Эллипс, гипербола, парабола
Если в уравнении F(x, y) = 0 линии на плоскости функция F(x, y) есть многочлен некоторой степени от двух переменных, то такая линия называется алгебраической, степень многочлена называется порядком кривой. Например, прямая – алгебраическая линия первого порядка. Рассмотрим линии второго порядка.
К кривым второго порядка относятся эллипс, гипербола и парабола. Эти кривые играют большую роль в прикладных вопросах.
Определение 1.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух фиксированных точек, принадлежащих этой же плоскости и называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Найдем уравнение эллипса. Для этого возьмем систему координат так, чтобы ось ОХ проходила через фокусы, а ось OY делила расстояние между фокусами пополам. Пусть расстояние между фокусами F1 и F2 равно 2 с, а сумма расстояний от текущей точки М(х, у) эллипса до фокусов равна 2 а: r 1 + r 2 = 2 a, 2 a > 2 с.
Тогда фокусы имеют координаты F1(с, 0) и F2(– с, 0), расстояния от т. М(х, у) до фокусов равны соответственно
r 1 = 
, r 2 = 
.
Из определения получаем уравнение эллипса
+ 
= 2 а
Упрощая это уравнение, получим
Полагая здесь а 2 – с 2 = b 2, получим уравнение
, (1)
которое называется каноническим уравнением эллипса.
Исследуем форму эллипса, используя это уравнение.
1) Нетрудно видеть, что если точка (х, у) принадлежит эллипсу, то ему принадлежат и точки (–х, у), (х, – у), (– х, – у), т.е. эллипс симметричен относительно осей координат и относительно начала координат.
2) Запишем уравнение (1) в виде 
откуда следует, что х Î[– a; a ], y Î [– b, b ].
3) В силу симметрии достаточно изучить характер линии при х Î[0; a ].
|
|
|
Когда х растет от 0 до а, 
убывает от b до 0, т.к. у ¢ = 
< 0 для всех х Î[0, a). Кроме того, кривая выпуклая: у ¢¢ = 
< 0 при х Î[0, a).
Учитывая эти исследования, построим график функции при х Î[0, a ] и отразим его симметрично относительно осей координат и начала координат.
Точки А, В, С, D пересечения эллипса с осями координат называются вершинами эллипса, точка О называется центром эллипса, отрезок АО = ОС = а называется большой полуосью, а ОВ = OD = b – малой полуосью эллипса, расстояния r 1 и r 2 от точки эллипса до фокусов называются фокальными радиусами.
Если бы мы расположили фокусы эллипса на оси ОУ, уравнение эллипса имело бы точно такой же вид, как и уравнение (1), только большой полуосью была бы b. В дальнейшем, договоримся, что большая полуось соответствует оси, на которой лежат фокусы эллипса и, наоборот, из уравнения эллипса по большему параметру а или b можно определить, на какой оси координат лежат фокусы эллипса.
На практике по заданному каноническому уравнению построить эллипс можно так: от начала координат влево и вправо по оси ОХ отложить отрезки длиной а, а по оси ОУ вверх и вниз – отрезки длины b. Через полученные точки-вершины провести гладкую замкнутую овальную линию.
Если а = b = 
, то с = 0, фокусы эллипса сливаются в одну точку – начало координат – и эллипс вырождается в окружность
х 2 + у 2 = а 2
с центром в начале координат и радиусом а.
Определение 2.
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний которых до двух заданных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Если расположить фокусы гиперболы на оси ОХ так, чтобы начало координат оказалось в середине между ними, обозначить расстояние между фокусами 2 с, модуль разности расстояний – 2 а, 2 a > 2 с, то символьное уравнение гиперболы будет иметь вид | r 1 – r 2| = 2 a, а в координатной форме оно запишется так:
|
|
|
½ – ½= 2 а.
Преобразовав это уравнение так же как в случае уравнения эллипса, и обозначив b 2 = с 2 – а 2, получим каноническое уравнение гиперболы
, (2).
Исследуя форму гиперболу, находим, что
1) кривая симметрична относительно осей и начала координат, поэтому исследование формы достаточно провести для части кривой, расположенной в первой четверти и являющейся графиком функции 
, х Î [ а, +¥), 
;
2) точки пересечения с осью ОХ (– а, 0) и (а, 0) – эти точки называются вершинами гиперболы; с осью ОУ кривая не пересекается;
3) 
прямые у =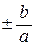 
являются асимптотами гиперболы. При изменении х от а до бесконечности функция возрастает от 0 до бесконечности, т.к. у ¢ = 
> 0 для всех х Î[ a, +¥). Кроме того, эта часть кривой выпуклая: у ¢¢= 
>0 при х Î[ a, +¥). Изобразив часть гиперболы в первой четверти в соответствии с этими исследованиями, затем отобразим эту линию симметрично относительно осей и начала координат на остальные четверти, получим искомую гиперболу.
 |
На практике по заданному каноническому уравнению гиперболу строят так.
1. Сначала строят осевой прямоугольник: слева и справа от начала координат на расстоянии а проводят прямые, параллельные оси ОУ, а сверху и снизу на расстоянии b от начала координат – прямые, параллельные оси ОХ.
2. Прямые, на которых лежат диагонали полученного прямоугольника, есть асимптоты гиперболы.
3. 
Точки пересечения сторон прямоугольника с осью ОХ – вершины гиперболы. От вершин к асимптотам в левой и правой полуплоскости проводят ветви гиперболы.
Точки А(– а, 0) и С(а, 0) называются вершинами гиперболы, точка О (начало координат) – центром гиперболы. Отрезок ОА = ОС = а называется действительной полуосью гиперболы, отрезок ОВ = OD = b – мнимой полуосью. Оси координат при этом так же называют соответственно действительной осью (ее гипербола пересекает в двух точках) и мнимой осью (ее гипербола не пересекает). Расстояния r 1 и r 2 от точки гипербол до фокусов называются фокальными радиусами.
Если фокусы гиперболы расположить на оси ОУ, то ее уравнение будет иметь вид
, или 
, (3).
|
|
|
где а –мнимая полуось, b – действительная. Гиперболы (2) и (3) называются сопряженными. Они имеют одни и те же асимптоты.
Таким образом, по каноническому уравнению гиперболы легко определить, какая из осей является действительной (ось, квадрат переменной которой входит в уравнение со знаком плюс), а какая – мнимой (квадрат соответствующей переменной входит со знаком минус).
Если а = b, гипербола называется равносторонней (равнобочной), ее асимптоты перпендикулярны друг другу.
Определение 3.
Параболой называется геометрическое место точек, равноудаленных от заданной точки (фокуса) и от заданной прямой (директрисы), лежащих в одной плоскости.
Найдем уравнение параболы, используя это определение.
Пусть р – расстояние между фокусом F и директрисой D. Расположим систему координат так чтобы директриса была параллельна оси ОУ, фокус находился на оси ОХ, начало координат располагалось посередине между фокусом и директрисой. Пусть М(х, у) – текущая точка параболы, фокус F(
,0), уравнение директрисы х =– , проекция точки М на директрису – точка К(– , х). Тогда символьное уравнение параболы |FM| = |MK| в координатной форме примет вид
.
После преобразований получаем у 2 = 2 рх.
Если фокус параболы поместить в точку F(– , 0), а директрисой взять прямую х = , то уравнение приобретет вид у 2 = –2 рх. Поэтому каноническим уравнением параболы называют уравнение вида
у 2 = 2 рх, (4)
где р – параметр произвольного знака.
Исследуем расположение параболы по ее каноническому уравнению (4).
1) Проходит через начало координат (0, 0).
2) Кривая симметрична относительно оси ОХ: точки (х, у) и (х, – у) принадлежат параболе. Ось ОХ при этом называют осью параболы.
3) В силу симметрии исследование достаточно провести при у > 0. Рассмотрим функцию 
, при р > 0 область определения этой функции х Î[0, +¥); при р < 0 область определения х Î(–¥, 0]. Производные этой функции равны у ¢ = 
, у ¢¢= 
.Для р >0 эта функция возрастает при х Î(0, +¥), убывает при х Î(–¥, 0), а в точке (0, 0) имеет минимум. Для р < 0, наоборот, при х Î(0, +¥) убывает, при х Î(–¥, 0) возрастает, в точке (0, 0) – максимум. Точку (0, 0) называют вершиной параболы. При р >0 и при у ¢¢ < 0, значит, кривая выпуклая.
|
|
|
4) По этим исследованиям вырисовывается следующая кривая
 |
Если фокус параболы расположить на оси ОУ, директрису провести параллельно оси ОХ, начало координат расположить по-прежнему посередине между фокусом и директрисой, то получим уравнение параболы в виде
х 2 = 2 ру, (5)
которое также называется каноническим уравнением параболы. Эта парабола имеет вершиной начало координат, осью симметрии ось ОУ; при р >0 ветви параболы направлены вверх, при р < 0 – вниз.
Свойства кривых второго порядка
Для всех рассмотренных кривых есть общая характеристика: фокус.
Фокус в переводе с латинского означает очаг. С фокусами кривых второго порядка связаны их оптические свойства
Представим себе, что эллипс, гипербола, парабола вращаются вокруг оси, содержащей фокусы. При этом образуется поверхность, которую называют соответственно эллипсоидом, гиперболоидом, параболоидом. Если реальную поверхность такого вида покрыть (со стороны фокусов) амальгамой, то получится соответственно эллиптическое, гиперболическое, параболическое зеркало. Известные из физики законы отражения света позволяют сделать такие выводы:
1) Если источник света поместить в одном из фокусов эллиптического зеркала, то его лучи, отразившись от зеркала, соберутся в другом фокусе.
Этим свойством пользовались фокусники: помещали источник света в одном фокусе эллиптического зеркала, в другом – воспламеняющееся вещество, которое загоралось без видимых причин, что поражало зрителей. Поэтому слово «фокус» получило тот смысл, в котором мы привыкли его употреблять.
2) 
Если источник света поместить в фокусе параболического зеркала, то его лучи, отразившись, пойдут параллельно оси параболы. На этом основано устройство прожектора.
3) 
Если источник света поместить в одном из фокусов гиперболического зеркала, то его лучи пойдут так, как если бы они исходили из второго фокуса.
Наряду с фокусами, характерными компонентами кривых второго порядка являются директрисы и эксцентриситет.
Определение 4.
Прямая D называется директрисой кривой, если отношение расстояния d от любой точки кривой до L к расстоянию r от этой точки до фокуса F кривой есть величина постоянная. Величина 
называется эксцентриситетом кривой.
Эллипс имеет две директрисы D 1 и D 2, расположенные вне эллипса, и перпендикулярные большой оси (параллельные малой) эллипса.
У гиперболы также две директрисы, расположены они между ветвями гиперболы перпендикулярно действительной оси (параллельно мнимой оси).
|
|
|
Уравнения директрис эллипса и гиперболы имеют вид 
, где а – большая или действительная полуось; директриса и фокус, расположенные по одну сторону от центра кривой, называются соответствующими друг другу. Постоянным является отношение расстояний от точки кривой до соответствующих друг другу фокусов и директрис.
У параболы один фокус и одна директриса, перпендикулярная оси параболы. Уравнения директрис в зависимости от расположения фокуса имеют вид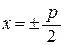 
.
Эксцентриситет кривой второго порядка характеризует форму этой кривой. Для эллипса эксцентриситет e < 1, для гиперболы e >1, у параболы e = 1, у окружности e = 0. Если а – большая или действительная полуось, с – половина фокусного расстояния, то эксцентриситет равен 
. Зависимость формы кривой второго порядка с одними и теми же фокусом и директрисой от эксцентриситета показана на рисунке:
|
|
|
