 |
Производная и дифференциал
|
|
|
|
Пусть функция 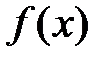 определена на промежутке
определена на промежутке 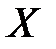 и
и 

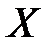 .
.
Определение 1. Если существует предел  , то он называется производной функции
, то он называется производной функции  в точке
в точке 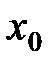 и обозначается
и обозначается 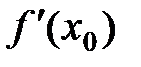 или
или  .
.
Операция нахождения (вычисления) производной называется дифференцированием.
Итак
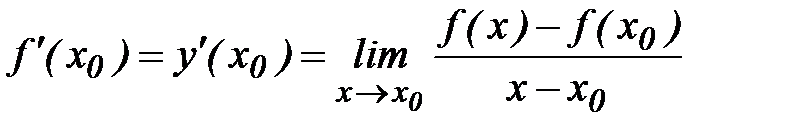 . (1)
. (1)
Если обозначить 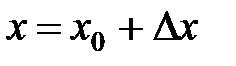 , то
, то  называется приращением аргумента,
называется приращением аргумента,  - приращением функции.
- приращением функции.
Теперь (1) можно записать в виде
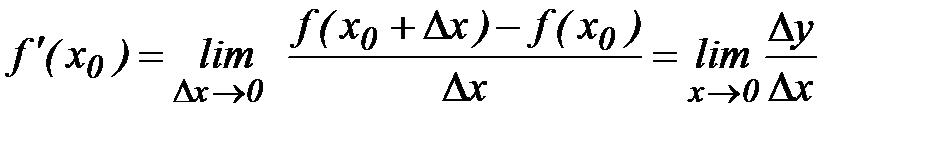 .
.
Пример. Найти производную функции  по определению.
по определению.
Решение. 
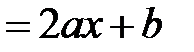 .
.
Если существуют левый и правый пределы в точке 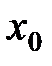 , т.е.
, т.е.
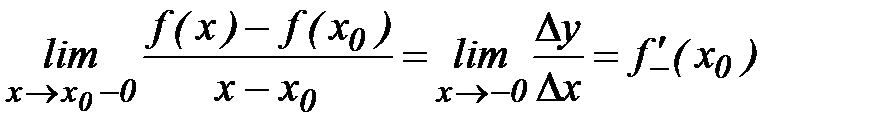 ,
,
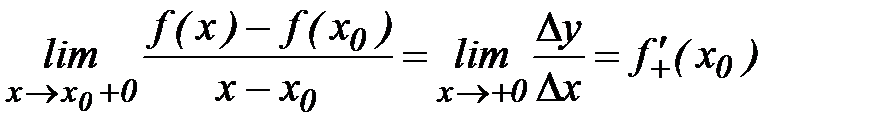 ,
,
то их называют левой и правой производной в точке  и обозначают
и обозначают 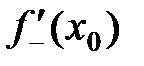 и
и  .
.
Ясно, что если существуют левая и правая производные в точке 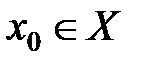 , причем
, причем 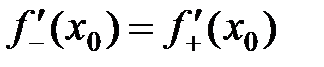 , то и
, то и 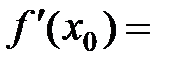
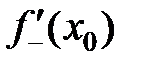 =
=  . Однако, если они не равны, то производная не существует.
. Однако, если они не равны, то производная не существует.
Пример. Найти производную функции 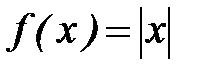 в точке
в точке 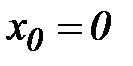 .
.
Решение. 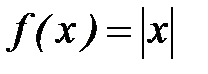 =
= 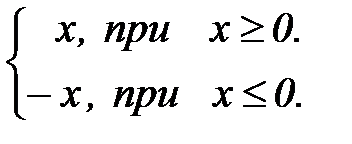
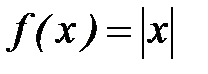 имеет
имеет 
 , поэтому
, поэтому 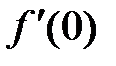 не существует.
не существует.
Определение 2. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 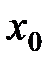 если она имеет в производную в этой точке. Функция
если она имеет в производную в этой точке. Функция  определенная на множестве
определенная на множестве  и дифференцируемая в каждой точке
и дифференцируемая в каждой точке 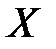 называется дифференцируемой на множестве
называется дифференцируемой на множестве 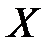 .
.
Пусть 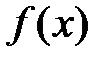 дифференцируема в точке
дифференцируема в точке 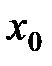 , тогда из формулы (1) ясно, что
, тогда из формулы (1) ясно, что
 .
.
Следовательно, в некоторой окрестности этой точки можно записать:
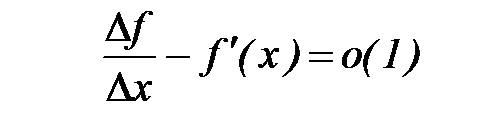 .
.
Тогда  , или
, или
 ,
,
или
 . (2)
. (2)
Теорема 1. Всякая дифференцируемая в точке 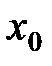 функция, непрерывна в этой точке.
функция, непрерывна в этой точке.
□ Из (2) следует что
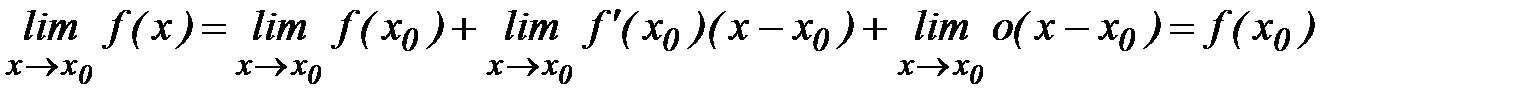 .
.
и, по определению непрерывности, теорема доказана. ■
По теореме, из дифференцируемости следует непрерывность, но не наоборот. Например, 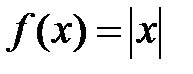 непрерывна в точке
непрерывна в точке 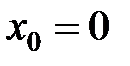 , но производной
, но производной 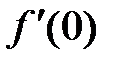 не существует.
не существует.
Пусть функция  дифференцируема в точке
дифференцируема в точке  , т.е. существует предел
, т.е. существует предел  . Тогда, как было показано, можно записать:
. Тогда, как было показано, можно записать:
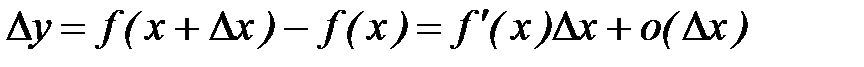 .
.
Здесь можно считать, что  есть функция относительно
есть функция относительно  .
.
Определение 3. Выражение  , линейное относительно переменной
, линейное относительно переменной 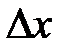 , называется дифференциалом (первым дифференциалом) функции
, называется дифференциалом (первым дифференциалом) функции 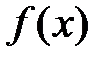 в точке
в точке 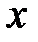 и обозначается
и обозначается 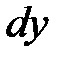 или
или 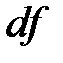 :
:
|
|
|
 ,
,  . (3)
. (3)
Поскольку если 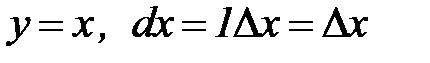 , то производную часто обозначают следующим образом:
, то производную часто обозначают следующим образом:
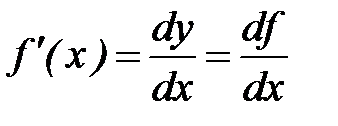 .
.
Формулу (3) можно записать 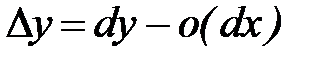 или
или 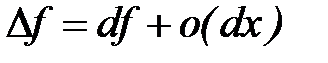 . Т.о. разность
. Т.о. разность  есть бесконечная малая более высокого порядка чем
есть бесконечная малая более высокого порядка чем  , т.е. дифференциал есть главная линейная часть приращения функции
, т.е. дифференциал есть главная линейная часть приращения функции 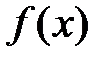 .
.
Т.к. при  , имеет место приближенная формула
, имеет место приближенная формула 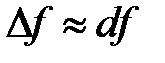 , то
, то 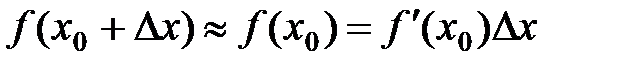 . Эта формула используется в приближенных вычислениях.
. Эта формула используется в приближенных вычислениях.
Пример. Вычислить приближенно  .
.
Пусть функция 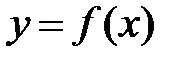 дифференцируема в точке
дифференцируема в точке 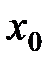 , т.е.
, т.е. 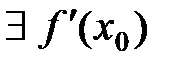 . На графике функции
. На графике функции 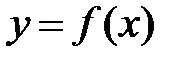 (рис.1) возьмем фиксированную точку
(рис.1) возьмем фиксированную точку 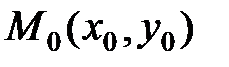 и зададим приращение
и зададим приращение 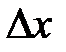 в точке
в точке 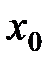 , т.е. рассмотрим текущую точку
, т.е. рассмотрим текущую точку 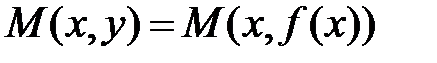 , где
, где 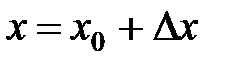 .
.
| y |

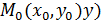
|
| M(x,y) |
| A |
 ) )
|
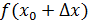
|
| α |
| φ |
| y=f(x,y) |
| O |

|

|
| x |
Рис. 1.
Обозначим 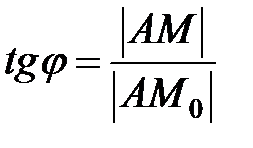 =
= 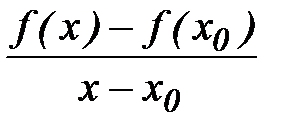 - угловой коэффициент секущей
- угловой коэффициент секущей  .
.
Если 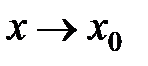 , то точка
, то точка 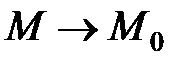 и
и 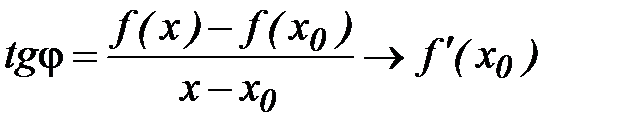 . Ясно, что
. Ясно, что
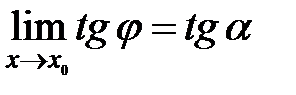 ,
,
где 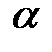 угол наклона касательной, т.е. предельного положения секущей, к положительному направлению оси
угол наклона касательной, т.е. предельного положения секущей, к положительному направлению оси 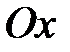 , проведенной в точке
, проведенной в точке 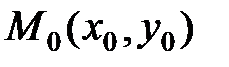 . С другой стороны
. С другой стороны
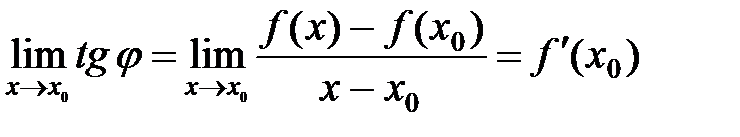 .
.
Откуда, следовательно, угловой коэффициент касательной прямой  равен значению производной
равен значению производной  в этой точке. В этом состоит геометрический смысл производной. Запишем уравнение касательной, воспользовавшись уравнением прямой с угловым коэффициентом:
в этой точке. В этом состоит геометрический смысл производной. Запишем уравнение касательной, воспользовавшись уравнением прямой с угловым коэффициентом:
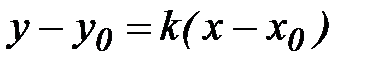 .
.
Тогда уравнение касательной прямой будет иметь вид:
 (4)
(4)
Замечание. Если 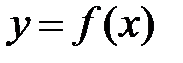 непрерывна в точке
непрерывна в точке 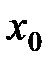 и
и  , то говорят, что
, то говорят, что 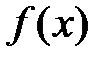 имеет в точке
имеет в точке 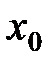 бесконечную производную и пишут
бесконечную производную и пишут  . В этом случае предельное положение секущей определяется уравнением
. В этом случае предельное положение секущей определяется уравнением 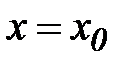 . Т.е. касательная параллельна оси
. Т.е. касательная параллельна оси 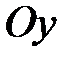 .
.
Рассмотрим физический смысл производной. Пусть точка движется прямолинейно вдоль оси  и
и  - её координата в момент времени
- её координата в момент времени  . Тогда
. Тогда  её путь, пройденный за отрезок
её путь, пройденный за отрезок 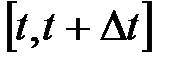 . Отношение
. Отношение 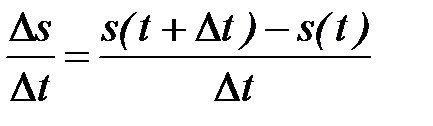 есть средняя скорость точки за время
есть средняя скорость точки за время  с момента
с момента  до момента
до момента  . Тогда предел (если он существует)
. Тогда предел (если он существует)
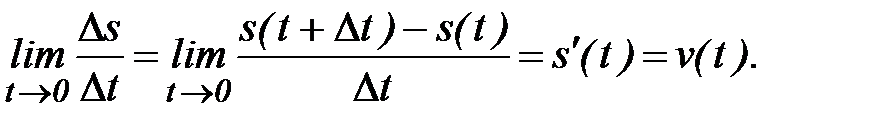
называется мгновенной скоростью точки в момент времени  и производная
и производная 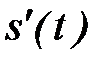 есть мгновенная скорость точки v(t) в момент времени
есть мгновенная скорость точки v(t) в момент времени 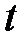 .
.
|
|
|
4.2. Правила дифференцирования.
Теорема 2 ( дифференцирование суммы, произведения и частного). Пусть функции  и
и 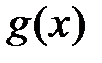 определены на промежутке X и дифференцируемы в точке
определены на промежутке X и дифференцируемы в точке  . Тогда в этой точке дифференцируемы функции
. Тогда в этой точке дифференцируемы функции
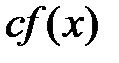 ;
; 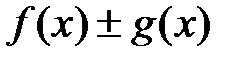 ;
; 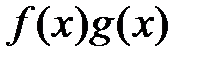 ;
; 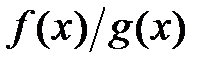 (
(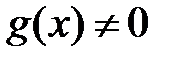 )
)
и имеют место формулы:
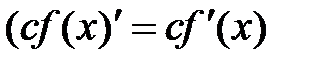 ;
;
 ;
;
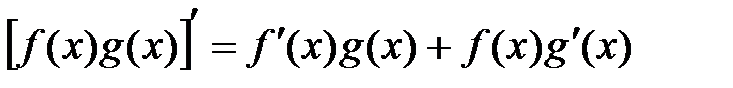 ;
;
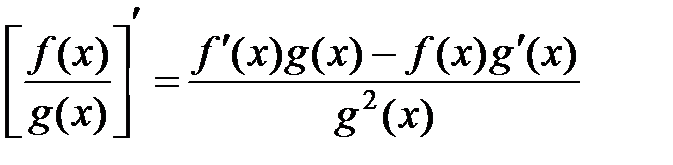 .
.
□ Докажем последнюю формулу (остальные самостоятельно). Пусть 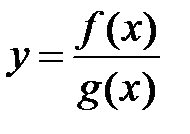 . Тогда
. Тогда
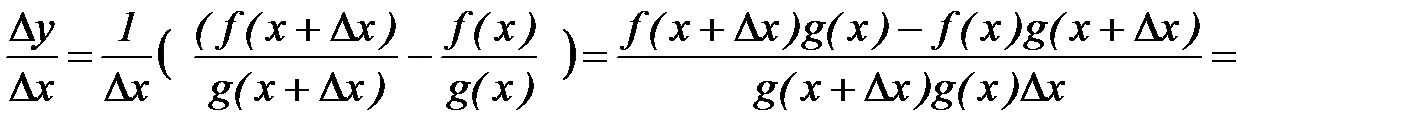

Перейдем к пределу, при 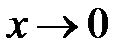 . В силу непрерывности
. В силу непрерывности 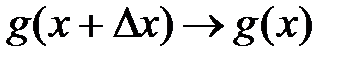 , а также в силу дифференцируемости:
, а также в силу дифференцируемости:  и
и 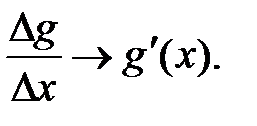 Откуда следует доказываемая формула. ■
Откуда следует доказываемая формула. ■
Замечание. Очевидно, что из определения 3 и теоремы 2 следуют аналогичные свойства для дифференциала:
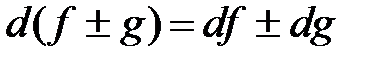 ;
; 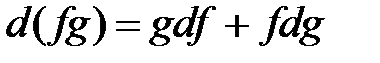 ;
; 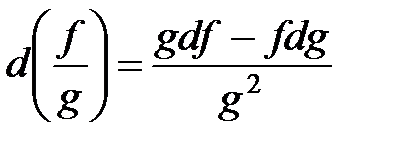
 ).
).
Теорема 3 (дифференцирование сложной функции). Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и дифференцируема в точке
и дифференцируема в точке 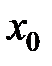 , а функция
, а функция 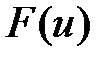 определена в точке
определена в точке 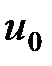 и дифференцируема в точке, причем
и дифференцируема в точке, причем 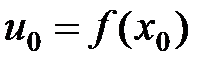 . Тогда сложная функция
. Тогда сложная функция 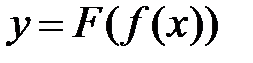 дифференцируема в точке
дифференцируема в точке 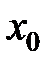 , причем справедлива формула:
, причем справедлива формула:
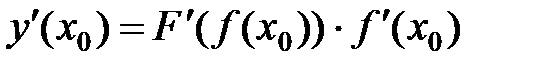
или
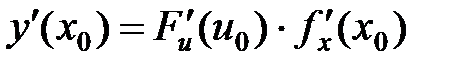
□ В силу дифференцируемости функции 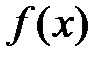 в точке
в точке  имеет место равенство (2):
имеет место равенство (2):
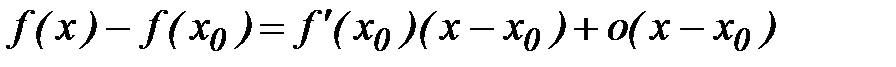 . (5)
. (5)
Т.к. 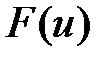 дифференцируема в точке
дифференцируема в точке 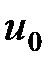 , то можно записать:
, то можно записать:
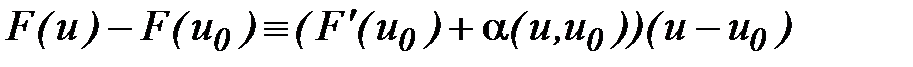 , (6)
, (6)
где  - бесконечно малая при
- бесконечно малая при 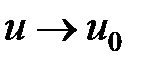 .
.
Если 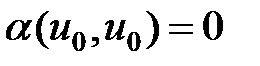 (положить равной), то
(положить равной), то  будет непрерывной в точке
будет непрерывной в точке  . Положим в (6)
. Положим в (6) 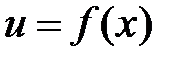 и
и 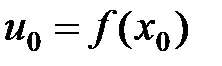 . Тогда, в силу (5) и (6), имеем
. Тогда, в силу (5) и (6), имеем

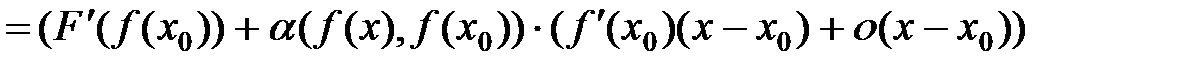 .
.
При 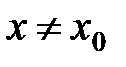 будет
будет
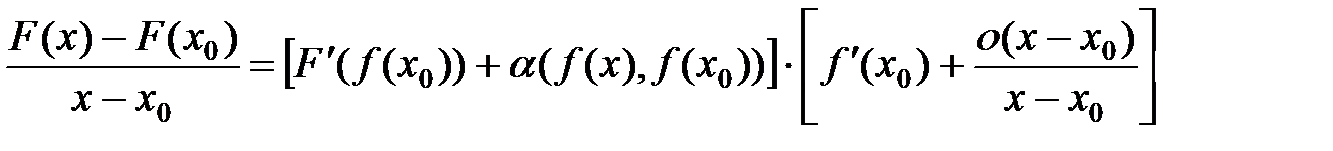 .
.
Переходя к пределу при 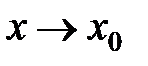 в силу непрерывности
в силу непрерывности 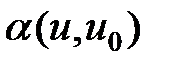 , при
, при 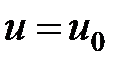 получим
получим  . ■
. ■
Пример. Найти производную функции 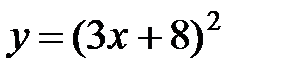 .
.
Обозначим 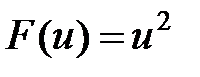 ,
, 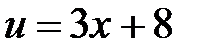 , тогда
, тогда 
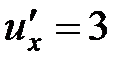 и по формуле имеем
и по формуле имеем  .
.
Рассмотрим сложную функцию 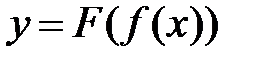 , для которой выполняются все условия теоремы о дифференцировании сложной функции. Тогда, с одной стороны, если
, для которой выполняются все условия теоремы о дифференцировании сложной функции. Тогда, с одной стороны, если  - независимая переменная, то
- независимая переменная, то
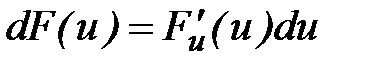 .
.
Но с другой стороны, если 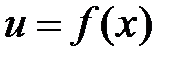 ,то
,то
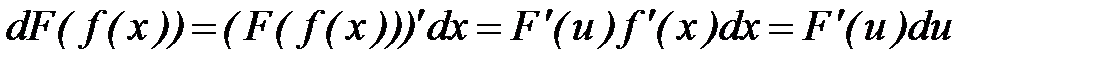 .
.
Таким образом., дифференциал функции 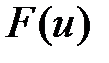 имеет один и тот же вид независимо является ли u независимой переменной или функцией какой-либо другой переменной. Это свойство называется свойством инвариантности формы первого дифференциала.
имеет один и тот же вид независимо является ли u независимой переменной или функцией какой-либо другой переменной. Это свойство называется свойством инвариантности формы первого дифференциала.
Теорема 4 ( дифференцирование обратной функции). Пусть  строго монотонна и непрерывная на промежутке
строго монотонна и непрерывная на промежутке 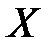 функция, дифференцируемая в точке
функция, дифференцируемая в точке  , причем
, причем 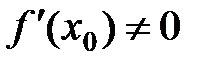 . Тогда обратная функция
. Тогда обратная функция 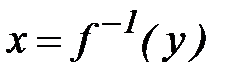 дифференцируема в точке
дифференцируема в точке 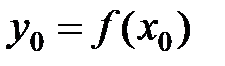 , причем
, причем 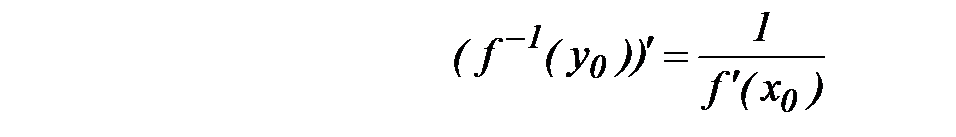 . (7)
. (7)
□ По теореме о непрерывности обратной функции, 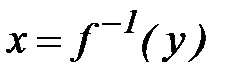 непрерывна на промежутке
непрерывна на промежутке 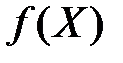 . Поэтому
. Поэтому 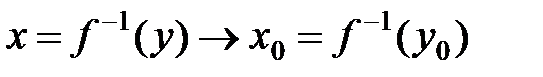 при
при 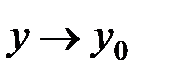 . Т.к.
. Т.к. 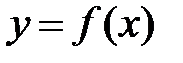 и
и 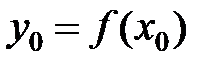 , то по определению производной имеют место равенства:
, то по определению производной имеют место равенства:
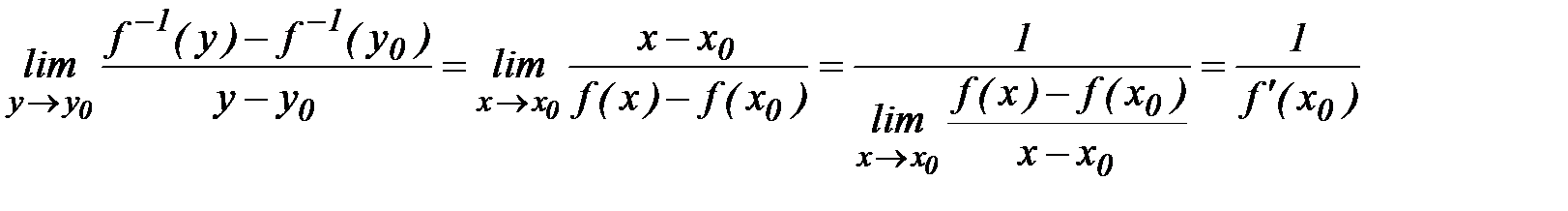 . ■
. ■
|
|
|
Пусть на промежутке  переменной
переменной 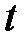 заданы две функции
заданы две функции
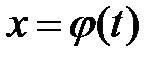 ,
, 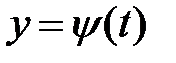 , (8)
, (8)
причем существует обратная функция  на
на 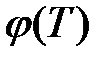 . Тогда следующая сложная функция
. Тогда следующая сложная функция 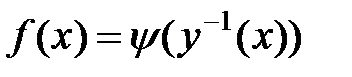 , определенная на
, определенная на 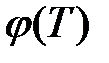 , называется параметрически заданной равенствами (8). Примерами функций, заданных параметрически являются следующие функции:
, называется параметрически заданной равенствами (8). Примерами функций, заданных параметрически являются следующие функции:
1) 
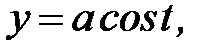
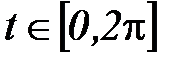 - окружность;
- окружность;
2) 
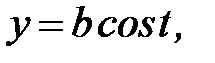
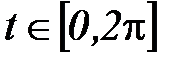 - эллипс;
- эллипс;
3) 
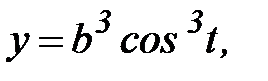
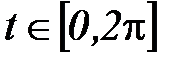 - астроида.
- астроида.
Теорема 5 ( дифференцирование параметрически заданной функции). Пусть строго монотонная и непрерывная на промежутке T функция 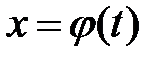 , дифференцируема в точке
, дифференцируема в точке 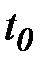 , причем
, причем  , а функция
, а функция 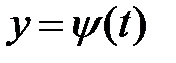 определена на промежутке
определена на промежутке  и дифференцируема в точке
и дифференцируема в точке 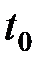 . Тогда сложная функция
. Тогда сложная функция 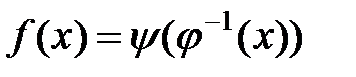 дифференцируема в точке
дифференцируема в точке 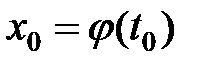 , и справедливо равенство:
, и справедливо равенство:
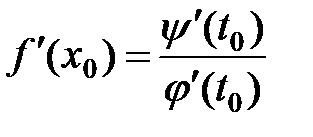 (
(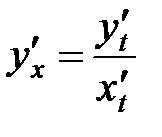 ). (9)
). (9)
В силу теоремы 4 обратная функция 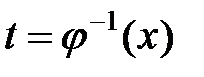 дифференцируема в точке
дифференцируема в точке 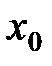 и
и 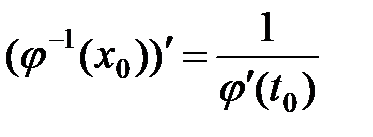
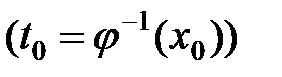 , а по теореме 3 функция
, а по теореме 3 функция 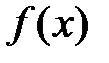 дифференцируема и производная равна:
дифференцируема и производная равна:
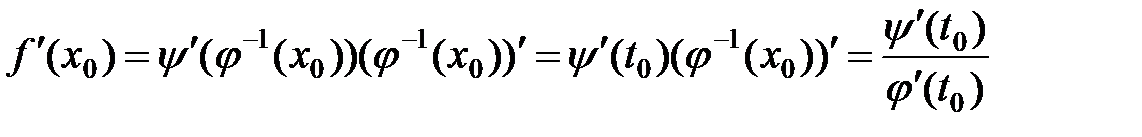 . ■
. ■
Пример. Вычислить производную по x функции, заданной параметрическими уравнениями: 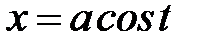 ,
, 
|
|
|


