 |
Теоремы о дифференцируемых функциях.
|
|
|
|
Теорема 6 ( Ролль). Пусть функция  удовлетворяет следующим условиям: а) непрерывная на отрезке
удовлетворяет следующим условиям: а) непрерывная на отрезке  ; б) дифференцируемая в интервале
; б) дифференцируемая в интервале  в)
в)  , тогда существует точка
, тогда существует точка 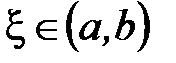 , такая, что
, такая, что  =0.
=0.
□ Если непрерывна на  , то по теореме Вейерштрасса существуют точные верхняя и нижняя грани M и m:
, то по теореме Вейерштрасса существуют точные верхняя и нижняя грани M и m: 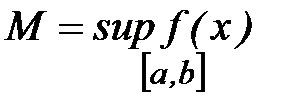
 . Если
. Если  :
:  .
.
Если 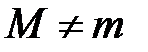 и какое-то из них не равно 0, то хотя бы одна из них достигается во внутренней точке, т.к.
и какое-то из них не равно 0, то хотя бы одна из них достигается во внутренней точке, т.к. 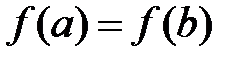 . Пусть в точке
. Пусть в точке  достигается наибольшее значение, т.е.
достигается наибольшее значение, т.е. 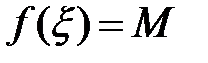 . Тогда
. Тогда 
 . Поэтому
. Поэтому
 при
при  ,
,
 при
при  .
.
Поскольку функция дифференцируемая, то 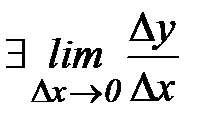 , который не зависит от
, который не зависит от 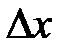 . Тогда переходя к пределу, по теореме сравнения получаем:
. Тогда переходя к пределу, по теореме сравнения получаем:


Это возможно, только если 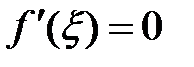 . ■
. ■
Геометрическая интерпретация теоремы: если на отрезке  значения в крайних точках равны, то на кривой
значения в крайних точках равны, то на кривой  существует точка, в которой касательная параллельна оси
существует точка, в которой касательная параллельна оси  .
.
Замечания. 1. Если 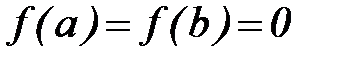 , то теорему можно сформулировать так: между всякими двумя нулями дифференцируемой функции лежит хотя бы один нуль производной. Именно так, причем лишь для многочленов она была сформулирована Роллем.
, то теорему можно сформулировать так: между всякими двумя нулями дифференцируемой функции лежит хотя бы один нуль производной. Именно так, причем лишь для многочленов она была сформулирована Роллем.
2. Если не выполняется одно из требований теоремы Ролля, то утверждение теоремы может оказаться неверным. Об этом свидетельствуют следующие примеры.
Примеры. 1)  ,
,  . Имеется разрыв в точке x =0.
. Имеется разрыв в точке x =0.
2)  ,
,  .
.
Функция непрерывна, но не дифференцируема на отрезке  , т.к.
, т.к. 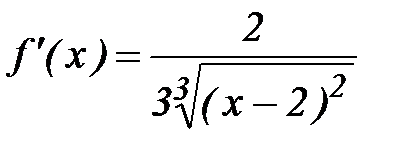 и в точке
и в точке  производной не существует, нет касательной параллельной оси
производной не существует, нет касательной параллельной оси  . Т.е. имеется излом границ, а, следовательно, касательную можно провести неоднозначно.
. Т.е. имеется излом границ, а, следовательно, касательную можно провести неоднозначно.
3)  . Не выполняется третье условие теоремы.
. Не выполняется третье условие теоремы.
Теорема 7 (Лагранж). Если функция  удовлетворяет условиям: а) непрерывна на отрезке
удовлетворяет условиям: а) непрерывна на отрезке 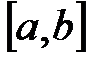 ; б) дифференцируема внутри него, то найдется хотя бы одна точка
; б) дифференцируема внутри него, то найдется хотя бы одна точка  , такая, что будет справедлива формула Лагранжа:
, такая, что будет справедлива формула Лагранжа:
 (11)
(11)
|
|
|
□ Рассмотрим на отрезке  вспомогательную функцию (разность ординат кривой и секущей, проходящей через точки f(a) и f(b)):
вспомогательную функцию (разность ординат кривой и секущей, проходящей через точки f(a) и f(b)):
 .
.
Для нее выполняются все условия теоремы Ролля:  -непрерывна, дифференцируема:
-непрерывна, дифференцируема:  и
и  . Тогда по теореме Ролля существует точка
. Тогда по теореме Ролля существует точка 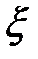 , где
, где 
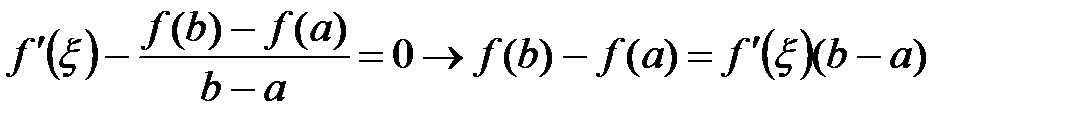 . ■
. ■
Геометрическая интерпретация: из(11) 
| y |
| a ξ b |
| y=f(x) |
| x |
| Рис.2. |
| Рис. |
| B |
| A |
Поскольку  угловой коэффициент секущей AB, стягивающей значения функции
угловой коэффициент секущей AB, стягивающей значения функции 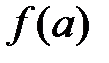 и
и  , то
, то  угловой коэффициент касательной в точке
угловой коэффициент касательной в точке  , и формула Лагранжа означает что внутри отрезка
, и формула Лагранжа означает что внутри отрезка  найдется хотя бы одна такая точка
найдется хотя бы одна такая точка  , в которой касательная параллельна хорде, стягивающей значения
, в которой касательная параллельна хорде, стягивающей значения 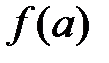 и
и  .
.
Замечание. Запишем формулу Лагранжа на отрезке  .
.
Пусть  , тогда из (11)
, тогда из (11)  . Если
. Если  или
или
 (12)
(12)
Формула(12) есть формула определения приращения функции через приращение аргумента. Поэтому формула (12) называется формулой конечных приращений.
Следствие 1. Если функция дифференцируема на промежутке  и
и 


□ Пусть  фиксированная точка
фиксированная точка  , а
, а  - произвольная точка. Тогда из (12) следует
- произвольная точка. Тогда из (12) следует 
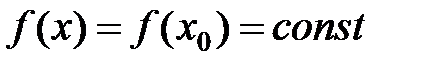 .
.
Следствие 2. Если функция  дифференцируема на промежутке
дифференцируема на промежутке  , тогда каждая точка
, тогда каждая точка  является либо точкой непрерывности, либо точкой разрыва 2-го рода. Иначе, производная
является либо точкой непрерывности, либо точкой разрыва 2-го рода. Иначе, производная 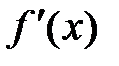 не может иметь точек устранимого разрыва и точек разрыва первого рода.
не может иметь точек устранимого разрыва и точек разрыва первого рода.
□ Пусть существует  . Проверим условие непрерывности производной в точке. По формуле (12):
. Проверим условие непрерывности производной в точке. По формуле (12): 
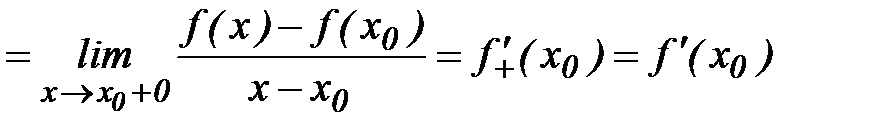 , т.е.
, т.е.  непрерывна справа в точке
непрерывна справа в точке  . Аналогично, доказывается непрерывность слева
. Аналогично, доказывается непрерывность слева  :
:
 .
.
Следовательно, если существует предел слева и справа равный  , то производная
, то производная  - непрерывна в точке
- непрерывна в точке 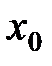 . Если хотя бы один из пределов не существует, то
. Если хотя бы один из пределов не существует, то 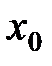 - точка разрыва второго рода. ■
- точка разрыва второго рода. ■
Теорема 8 (Коши). Если функции  и
и  обладают следующими свойствами: а) непрерывны на отрезке
обладают следующими свойствами: а) непрерывны на отрезке  ; б) дифференцируемы во всех его внутренних точках; в)
; б) дифференцируемы во всех его внутренних точках; в)  , то внутри существует такая точка
, то внутри существует такая точка  , что справедлива формула Коши:
, что справедлива формула Коши:
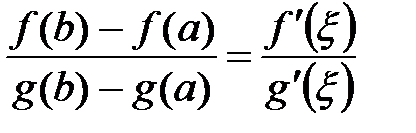 . (13)
. (13)
□ Ясно, что  . Действительно, пусть
. Действительно, пусть  , тогда для неё выполняются все условия теоремы Ролля, следовательно
, тогда для неё выполняются все условия теоремы Ролля, следовательно  , что
, что 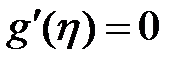 . Однако это по условию невозможно. Следовательно
. Однако это по условию невозможно. Следовательно  . Тогда рассмотрим вспомогательную функцию:
. Тогда рассмотрим вспомогательную функцию:
|
|
|
 .
.
Для неё выполняются все условия теоремы Ролля (проверить). Тогда для 
 , что
, что  :
:
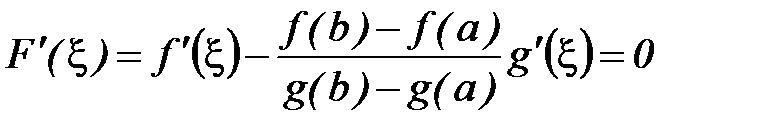 .
.
Откуда следует формула (13). ■
Заметим, что формула Лагранжа является частным случаем формулы Коши при 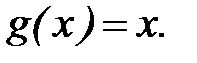
4.6. Контрольные вопросы
1. Дайте определение производной функции  в точке
в точке  .
.
2. Каков геометрический смысл производной функции  в точке
в точке  ?
?
3. Дайте определение касательной к графику функции  в точке
в точке  и напишите уравнение касательной.
и напишите уравнение касательной.
4. Каков физический смысл производной функции  в точке
в точке  ?
?
5. Дайте определение правой (левой) производной функции  в точке
в точке  . Какова связь между односторонними производными и производной функции в точке
. Какова связь между односторонними производными и производной функции в точке  ? Приведите пример функции, у которой существуют правая и левая производные в некоторой точке, но не существует производная в этой точке.
? Приведите пример функции, у которой существуют правая и левая производные в некоторой точке, но не существует производная в этой точке.
6. Дайте определение дифференцируемости функции в точке  .
.
7. Какова связь между понятиями дифференцируемости функции в точке и производной функции в этой точке? Докажите соответствующую теорему.
8. Какова связь между понятиями дифференцируемости и непрерывности функции в точке? Приведите пример функции, непрерывной в точке, но не дифференцируемой в этой точке.
9. Может ли функция, имеющая производную в точке, быть непрерывной в этой точке?
10. Дайте определение дифференциала функции в точке  .
.
11. Почему в определении дифференциала выражение  называется главной, линейной относительно
называется главной, линейной относительно 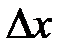 частью приращения функции
частью приращения функции  ?
?
12. Каков геометрический смысл дифференциала?
13. Докажите правила дифференцирования суммы, разности, произведения и частного двух функций.
14. Что можно сказать, если выполнены все условия теоремы о правилах дифференцирования, кроме условия  , т. е. выполнено условие
, т. е. выполнено условие  ?
?
15. Почему при доказательстве правил дифференцирования произведения и частного 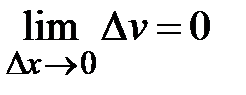 ?
?
16. Сформулируйте теорему о производной обратной функции.
17. Что можно сказать о производной обратной функции, если  ? Приведите пример такого случая
? Приведите пример такого случая
18. Каков геометрический смысл теоремы о производной обратной функции?
19. Сформулируйте теорему о производной сложной функции.
|
|
|
20. Применима ли теорема о производной сложной функции к функции  в точке
в точке  ? Существует ли производная этой функции в точке
? Существует ли производная этой функции в точке  ?
?
21. Что такое параметрическое задание функции?
22. При каких условиях справедлива формула для производной функции, заданной параметрически.
23. Выведите формулы для производных постоянной, степенной, тригонометрических функций и логарифмической функции.
24. Почему при выводе формулы производной логарифмической функции знаки функции и предела поменяли местами?
25. Выведите формулы производных для показательной функции и обратных тригонометрических функций.
26. Почему при выводе формулы производной для показательной функции функция  является обратной для функции
является обратной для функции 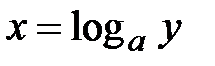 ?
?
27. В чем состоит прием логарифмического дифференцирования?
28. Выведите формулу производной для степенной функции с любым вещественным показателем.
29. Почему операция дифференцирования не выводит из класса элементарных функций?
30. Докажите, что  .
.
31. Почему производную  можно рассматривать как функцию аргумента
можно рассматривать как функцию аргумента 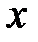 ?
?
32. Дайте определение второй производной функции  .
.
33. Приведите пример функции, у которой существует  , но не существует
, но не существует  .
.
34. Является ли производная  непрерывной функцией в точке
непрерывной функцией в точке  , если в этой точке существует
, если в этой точке существует  ?
?
35. Дайте определение  -й производной функции
-й производной функции  .
.
36. Известно, что 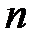 -я производная функции
-я производная функции 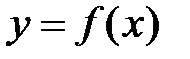 существует в точке
существует в точке  . Что можно сказать о существовании производных меньшего порядка в этой точке и ее окрестности?
. Что можно сказать о существовании производных меньшего порядка в этой точке и ее окрестности?
37. Дайте определение  -го дифференциала функции
-го дифференциала функции  .
.
38. Сформулируйте теорему Ролля и раскройте ее геометрический смысл.
39. Останется ли справедливой теорема Ролля, если опустить одно из ее трех условий? Приведите соответствующие примеры.
40. Сформулируйте теорему Лагранжа и объясните ее геометрический смысл.
41. Сформулируйте теорему Коши.
42. Покажите, что теорема Лагранжа является частным случаем теоремы Коши.
|
|
|


