 |
Элементарная теория дисперсии
|
|
|
|
Из макроскопической электромагнитной теории Максвелла следует, что 
Для большинства прозрачных сред m = 1, поэтому 
. Отсюда выявляются некоторые противоречия: величина n, являясь переменной, остается в то же время равной определенной постоянной. Кроме того, значения n, получаемые из этого выражения, не согласуются с опытом. Трудности объяснения дисперсии света с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном поле волны.
Под действием поля Е световой волны электронные оболочки атомов деформируются. Они становятся диполями с моментами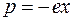 
, где е – заряд электрона, х – смещение электрона. Если в единице объема N атомов, то дипольный момент: 
.
Зная Р, можно вычислить e среды:
. (3)
Найдем смещение электрона x под действием внешнего поля волны. В первом приближении можно считать, что вынужденные колебания совершают только оптические электроны, наиболее слабо связанные с ядром атома.
Уравнение вынужденных колебаний электрона запишем на основании 2-го закона Ньютона: 
. Учтем, что на электрон будут действовать силы:
1. Квазиупругая сила, возвращающая (удерживающая) электрон в состоянии покоя 
.
2. Сила трения излучения 
3. Внешняя периодическая сила 
, где 
, тогда
, 
, 
или
. (4)
Пренебрежем для простоты расчетов силой трения излучения: 
, где 
– собственная частота колебаний электрона.
Из механики известно, что решением этого дифференциального уравнения является выражение:
, (5)
где 
– амплитуда вынужденных колебаний электрона. Подставляя (5) в (3), окончательно получим:
|
|
|
. (6)
Из (6) следует, что при приближении частоты электромагнитной волны ω к собственной частоте электронов в молекуле справа и слева показатель преломления стремится к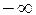 
или 
, соответственно. Это происходит потому, что мы пренебрегли трением излучения. Учет этой силы несколько меняет характер зависимости.
 |
Таким образом, вблизи собственной частоты функция
терпит разрыв, в этой области наблюдается сильное поглощение электромагнитных волн.
При переходе от к 
, получим зависимость несколько иного вида. Пунктирная кривая характеризует поглощение света в области данной длины волны 
. Участки 1-2 и 3-4 – 
нормальная дисперсия: n убывает с ростом λ и 
. На участке 2-3 наблюдается аномальная дисперсия 
и n растет с ростом λ. Кроме того, легко заметить, что на участке 1-2 
, следовательно, фазовая скорость волны будет больше скорости света в данной среде. Это не противоречит теории относительности, поскольку υ – фазовая скорость, с которой энергия (а значит и масса) не переносится, как и информация.
Если учесть все заряды атомов, то из (6) получим:
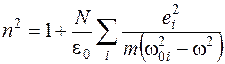. (5)
Здесь суммирование производится по всем видам зарядов. Таким образом, аномальная дисперсия объясняется резонансным поглощением световой волны. Более детальным является расчет дисперсии на основе квантово-механической теории, согласно которой ω0 принимает дискретный набор значений. Исследуя n (ω), и, находя из опыта частоты ω0, можно получить ценную информацию о структуре и свойствах электронных оболочек атомов и молекул вещества.
Таким образом, зависимость n (ω) или n (λ) для белого света можно использовать, чтобы определить спектральный состав света. Для этого лучше всего взять узкий пучок света и направить его на призму. Тогда при одном и том же угле падения всех длин волн (частот) углы преломления, а значит и расположение их на экране будет упорядоченным. Такой прибор называют призменным монохроматором, поскольку он позволяет получать свет нужной длины волны или частоты. Его можно использовать для определения длин волн источников излучения, качественного и количественного спектрального анализа оптически прозрачных сред.
|
|
|
Прибор состоит из источника света, который направляется на входную щель с колпаком, а затем на входной объектив и диспергирующую призму. Призму можно поворачивать с помощью барабана с нанесенными на него делениями N со шкалой. Она фокусирует свет на выходную щель. Затем свет через линзу попадает в глаз наблюдателя. Перемещение этой линзы можно определять с помощью шкалы нониусов, а осуществлять – специальным винтом, установленным на объективе.
Порядок выполнения работы:
|
|
|
