 |
Законом распределения называют соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
|
|
|
|
Таблица 1
Интервальный вариационный ряд
| Номер интер- вала | Границы интервала | Частота (число вариантов в i-ом интервале mi | Частость
|
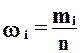
| . k |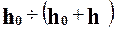 
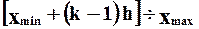
| m1 m2 . mk | ω1 ω2 ω3 . ωk |
| 
|
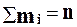
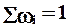
Частостью называется относительная частота попадания СВ в i‑й интервал (число значений СВ в определенном интервале, отнесенное общему объему выборки).
6) В масштабе строят ГИСТОГРАММУ – ступенчатую фигуру, состоящую из прямоугольников с основанием в виде отрезков, соответствующих длинам интервалов, и высотами, соответствующими частостям.
7) Определяют ЗАКОН РАСПРЕДЕЛЕНИЯ СВ.
ЗАКОНОМ РАСПРЕДЕЛЕНИЯ называют соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Закон распределения может быть представлен таблично, аналитически и графически.
Наиболее просто и наглядно, хотя в определенной степени субъективно и приближенно, представлять закон распределения графически на основе гистограммы.
Действительно, если необходимое число интервалов разбиения выборки определять по формуле Стерджеса (по формуле 2), то очевидно, что для теоретической генеральной совокупности, т.е. при n → ∞, число интервалов k также будет стремиться к бесконечности (k → ∞), хотя и с меньшей скоростью. С ростом числа интервалов, будет уменьшаться их длина и, таким образом, ломаная линия гистограммы превратится в плавную кривую (рис. 2).
При этом относящееся к выборке понятие частость (ωi) для генеральной совокупности заменяется на понятие вероятность (ρi):
при n → ∞ ωi = ρi.
Например, вероятность того, что СВ примет значение xi равна ρi.
|
|
|
Известно, что:
Ø ошибки измерений,
Ø результаты измерений,
Ø результаты обработки долот,
Ø показатели буримости пород,
Ø механическая скорость проходки Vм,
Ø показатели свойств промывочных жидкостей
Ø показатели свойств тампонажных смесей,
Ø интенсивность зенитного искривления
и многие другие показатели, характеризующие процессы бурения, подчиняются нормальному закону распределения (закону Гаусса), который является основным законом в теории вероятности.
Нормальный закон распределения СВ имеет следующие особенности:
1. Количество вариантов (значений СВ), превышающих среднее значение, равно количеству вариантов, которые меньше его (примерная симметричность гистограммы).
2. Частота вариантов тем больше, чем ближе к среднему значению они расположены - гистограмма имеет наибольшие ординаты в центре и наименьшие – у краев (рис. 3).
Особая роль нормального закона (НЗ) среди прочих законов распределения обусловлена следующими причинами:
Ø Нормальный закон хорошо изучен, а посему методика обработки данных, подчиняющихся этому закону, достаточно полно разработана и относительно проста (именно поэтому на начальном этапе обработки экспериментальных данных важно убедиться в том, что их распределение подчиняется нормальному закону).
Ø При увеличении объема данных (объема выборки) целый ряд других законов распределения (Стьюдента, x2 – хи ‑ квадрат и др.) стремятся превратиться в нормальный закон.
Отсюда следует вывод, что если результаты измерений вызывают сомнение в нормальности закона их распределения, то для решения вопроса о пригодности или непригодности этого закона нужно увеличить объем выборки (число измерений).
По своему виду кривые нормального распределения могут быть:
Ø нормальновершинными;
Ø туповершинными;
Ø островершинными (рис. 4).
|
|
|
Ø иметь положительную асимметрию (рис.5а);
Ø иметь отрицательную асиметрию (рис.5б).
В практике бурения приходится иметь дело и с явно асимметричными кривыми (законами) распределения.
Рассмотрим два из них:
a) Логарифмически нормальный (ЛНЗ), имеющий умеренно асимметричную кривую распределения;
b) Показательный (экспоненциальный), имеющий резко асимметричную кривую распределения.
Логарифмически - нормальное распределение чаще всего имеет место, когда значения СВ ограничены некоторыми пределами.
Например, величина выхода керна ограничена сверху значением 100%, а снизу ‑ 0%. В породах, где значения выхода керна в среднем далеки от этих пределов (например, если средний выход керна составляет 50%), распределение может быть близким к нормальному.
В то же время в крепких и монолитных породах, где выход керна близок к верхнему пределу (100%), распределение будет явно асимметричным и сдвинутым в сторону больших значений СВ (рис. 6,а).
В рыхлых нецементированных породах, где выход керна близок к нулю, будет наблюдаться правосторонняя асимметрия распределения (рис.6,б).
Если случайная величина x подчинена логарифмически - нормальному закону, то из этого следует, что величина 
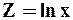распределена нормально (т.е. исходные данные необходимо прологарифмировать).
Показательное (экспоненциальное) распределение имеет место лишь при определении характеристик надежности и долговечности бурового оборудования, инструмента, приборов, средств механизации производственных процессов и т.п.
|
|
|
