 |
Находят точечные оценки параметров нормального распределения СВ.
|
|
|
|
Правила определения оценок для параметров нормального распределения по совокупности независимых измерений СВ регламентируются ГОСТ 11.004 ‑ 74.
Наиболее достоверной оценкой измаеряемой СВ является ее СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ИЛИ СРЕДНЕЕ ВЗВЕШАННОЕ ЗНАЧЕНИЕ.
Среднее арифметическое значение определяется тогда, когда все варианты (значения СВ) имеют одну и ту же частоту, равную единице (нет одинаковых значений СВ), что характерно для малых выборок.
Если варианты имеют различные частоты, что характерно для больших выборок, то рассчитывают среднее взвешанное значение СВ по следующей формуле:
(5)
где:
Ø 
- значение варианта (СВ) в середине i ‑го интервала вариационного ряда;
Ø mi – частота (число вариантов СВ), соответствующая i ‑ му интервалу;
Ø k – число интервалов.
Наряду со средним взвешенным значением СВ в качестве характеристик вариационного ряда, дающих информацию о законе распределения, используют МЕДИАНУ И МОДУ.
Медиана (m0,5) – это значение СВ, которое делит вариационный ряд или площадь, ограниченную кривой распределения, на две равные части.
При нечетном объеме выборки медиана равна
, (6)
а при четном объеме
, (7)
где:
xm – значение средней по порядку вариационного ряда случайной величины.
(Например, если в вариационном ряду 51 значение случайной величины, то m0,5 будет равна значению 26, если 50 – то 25)
Модой m0 называют варианту, которая имеет наибольшую частоту, т.е. соответствует вершине распределения (это наиболее вероятное значение случайной величины).
Оценивают моду по следующей формуле
, (8)
где:
- нижняя граница модального интервала, т.е. интервала, имеющего
наибольшую частоту;
h – длина интервала разбиения (шаг);
|
|
|
- частота модального интервала;
- частота интервала, предшествующего модальному интервалу;
- частота интервала, следующего за модальным интервалом.
Для нормального симметричного распределения
(9)
Весьма важной характеристикой нормального распределения является СТЕПЕНЬ РАЗБРОСА (РАССЕИВАНИЯ) ОТДЕЛЬНЫХ ЧАСТЕЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОТНОСИТЕЛЬНО ЕЕ СРЕДНЕГО ЗНАЧЕНИЯ.
Для оценки степени разброса пользуются несколькими показателями, из которых наиболее широко распространены следующие:
Ø РАЗМАХ (R), представляющий собой разность между наибольшим (xmax) и наименьшим (xmin) значениями вариант (см. формулу 1).
Ø ДИСПЕРСИЯ (D) – это среднее арифметическое значение квадратов отклонений отдельных вариант от их средней арифметической.
Оценивается дисперсия по следующей формуле:
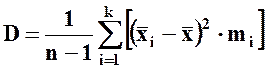(10)
где:
· 
- значение СВ в середине i ‑ го интервала;
· 
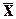- среднее взвешенное значение СВ;
· mi – частота соответствующая i ‑ му интервалу;
· k – число интервалов;
· n – объем выборки.
Ø СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ (s) – это значение корня квадратного из дисперсии.
. (11)
Ø КОЭФФИЦИЕНТ ВАРИАЦИИ (
) – это отношение среднего квадратического отклонения к среднему значению СВ, выраженное в процентах
. (12)
Чем больше коэффициент вариации , тем больше разброс значений СВ вокруг среднего значения, тем менее представительно .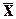 
Принято считать, что инструментальные лабораторные исследования обеспечивают n £ 8%. Экспериментальные исследования в производственных условиях обычно дают n £ 8 - 15%..
В бурении n, как правило, находится в пределах от 12 до 27%.
В зависимости от величины коэффициента вариации технологические показатели и расчеты разбиты на 5 классов точности.
| Класс точности | |||||
| n,% | < 8 | 8 - 15 | 15 - 25 | 25 - 35 | > 35 |
|
|
|
