 |
Временное дискриминирование импульсного сигнала
|
|
|
|
1. Дискриминационная характеристика
В предыдущей лабораторной работе отмечались недостатки дифференцирования сигнала как метода оценивания его временного положения. Временное дискриминирование [1] можно считать своеобразным обобщением дифференцирования, компенсирующим его недостатки. В том числе может фиксироваться время прихода  протяжённого сигнала. Временное дискриминирование применяется главным образом в системах слежения [2,3].
протяжённого сигнала. Временное дискриминирование применяется главным образом в системах слежения [2,3].
Под временем прихода  понимают момент времени, соответствующий некоторой характерной точке сигнала, например, амплитуде или средней точке (рис. 1,
понимают момент времени, соответствующий некоторой характерной точке сигнала, например, амплитуде или средней точке (рис. 1,  - мода сигнала – момент амплитуды
- мода сигнала – момент амплитуды
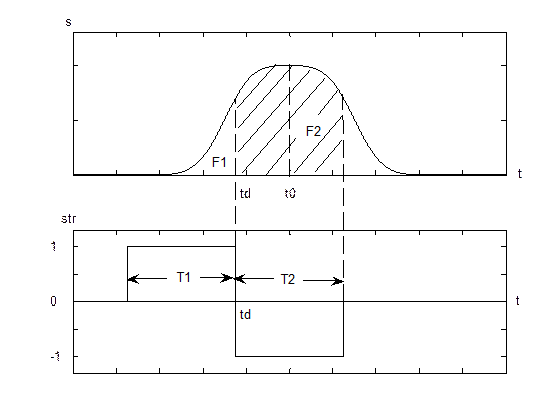
Рис. 1. Временное дискриминирование
Временное дискриминирование. базируется на двух стробирующих импульсах (полустробы  , рис. 1) длительностью
, рис. 1) длительностью 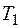 и
и 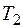 . Для симметричного импульса
. Для симметричного импульса  . Входной сигнал (сумма шума
. Входной сигнал (сумма шума 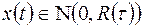 и сигнала
и сигнала  )
)
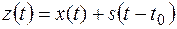
интегрируется в пределах длительности полустробов
 ,
,  ,
,
 - временное положение стробов. Разность интегралов
- временное положение стробов. Разность интегралов
 (1)
(1)
характеризует время прихода. Между стробирующими импульсами может быть некоторый интервал.
Пусть сигнал симметричен, шум отсутствует. Разность (1)

 -
-  (2)
(2)
равна нулю при 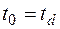 , отрицательна при
, отрицательна при 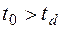 , положительна при
, положительна при  (рис. 2,
(рис. 2, 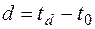 ). Функция (2) называется дискриминационной характеристикой.
). Функция (2) называется дискриминационной характеристикой.
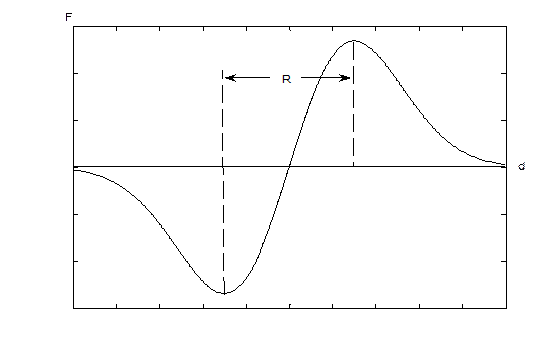
Рис. 2. Дискриминационная характеристика
Система слежения за импульсами работает по последовательности импульсов неизменной формы с неизвестными интервалами между ними. Интервалы неизвестны, например, в радиолокационной системе слежения за маневрирующей целью. Нулевая точка дискриминационной характеристики и точка 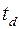 стробирующих импульсов совпадают. Эти точки на оси времени располагаются в предполагаемой моде очередного ожидаемого импульса (рис.3). Но истинная мода
стробирующих импульсов совпадают. Эти точки на оси времени располагаются в предполагаемой моде очередного ожидаемого импульса (рис.3). Но истинная мода 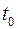 пришедшего сигнала окажется в другой точке:
пришедшего сигнала окажется в другой точке:
|
|
|
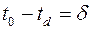 .
.
Интегрирование (2) пришедшего сигнала даст значение  (рис. 3), которому и будет соответствовать мода пришедшего сигнала.
(рис. 3), которому и будет соответствовать мода пришедшего сигнала.

Рис. 3. Ошибка измерения моды сигнала
Предполагается, что мода следующего сигнала тоже будет равна 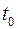 , поэтому дискриминационная характеристика вместе со стробами сдвигается в точку
, поэтому дискриминационная характеристика вместе со стробами сдвигается в точку 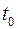 , и процесс повторяется. Если зондирующие сигналы радиолокатора повторяются достаточно часто, ошибка
, и процесс повторяется. Если зондирующие сигналы радиолокатора повторяются достаточно часто, ошибка 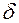 измерения моды сигнала будет уменьшаться. Если частота зондирующих сигналов недостаточна, мода очередного сигнала может выйти за пределы рабочей области
измерения моды сигнала будет уменьшаться. Если частота зондирующих сигналов недостаточна, мода очередного сигнала может выйти за пределы рабочей области  дискриминационной характеристики (рис. 2), и произойдёт срыв слежения.
дискриминационной характеристики (рис. 2), и произойдёт срыв слежения.
Шум вызывает погрешность за счет случайного смещения моды.. При большом отношении сигнал – шум дисперсия погрешности измерений [2]
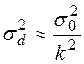 , (3)
, (3)
 - дисперсия случайной составляющей дискриминационной характеристики,
- дисперсия случайной составляющей дискриминационной характеристики,
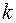 - крутизна дискриминационной характеристики в окрестности
- крутизна дискриминационной характеристики в окрестности  . Наличие шума вызывает необходимость увеличения частоты зондирующих сигналов, но этого недостаточно для надёжного слежения – всегда существует ненулевая вероятность срыва слежения.
. Наличие шума вызывает необходимость увеличения частоты зондирующих сигналов, но этого недостаточно для надёжного слежения – всегда существует ненулевая вероятность срыва слежения.
2. Флюктуационная составляющая дискриминационной характеристики
Случайная (флюктуационная) составляющая дискриминационной характеристики формируется по тому же правилу (2), что и сама дискриминационная характеристика:

 -
- 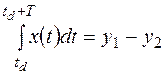 . (4)
. (4)
Вследствие линейности интегральных преобразований
 ,
, 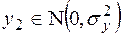 ,
,  ,
,
дисперсия случайной составляющей дискриминационной характеристики
 , (5)
, (5)
 - корреляционный момент величин
- корреляционный момент величин  и
и  .
.
3. Моделирование дискриминатора
Расчет дискриминационной характеристики (2) принципиальных трудностей не представляет, хотя интегрирование довольно громоздко. Избежать математических трудностей позволяет моделирование дискриминатора с использованием дискретных сигналов и численного интегрирования. MATLAB - программы, в том числе программа расчета дискриминационной характеристики, приведены в [3].
|
|
|
Задаются форма сигнала и функция корреляции стационарного аддитивного шума. Порядок моделирования:
1) рассчитывается дискриминационная характеристика, вычисляется ее крутизна;
2) рассчитывается дисперсия (5);
3) формируются 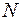 реализаций флюктуационной характеристики;
реализаций флюктуационной характеристики;
4) по 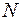 реализациям флюктуационной характеристики оценивается время прихода сигнала и его дисперсия.
реализациям флюктуационной характеристики оценивается время прихода сигнала и его дисперсия.
Флюктуационная составляющая (4) моделируется по той схеме, что дискриминационная характеристика: генерируется реализация дискретного случайного процесса с функцией корреляции протяженностью  отсчетов; интегрированием в полустробах и вычитанием формируются
отсчетов; интегрированием в полустробах и вычитанием формируются 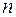 отсчетов флюктуационной составляющей, которые суммируются с
отсчетов флюктуационной составляющей, которые суммируются с 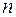 отсчетами дискриминационной характеристики; процесс повторяется
отсчетами дискриминационной характеристики; процесс повторяется 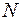 раз – формируются множество реализаций размерностью
раз – формируются множество реализаций размерностью 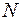 строк
строк 
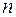 столбцов.
столбцов.
В [3] приведен пример с сигналом (рис. 1)
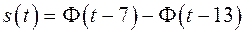 ,
,
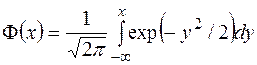 ,
,
и длительностью полустробов  . Шум задан как аддитивный стационарный гауссов процесс с функцией корреляции
. Шум задан как аддитивный стационарный гауссов процесс с функцией корреляции
 .
.
Число отсчетов настраивается по графикам вида изображенных на рис. 4.

Рис. 4. Сигнал с амплитудой 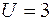 ,
,
дискриминационная характеристика с крутизной 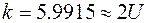
Искажения дискриминационной характеристики иллюстрируются на рис. 5: 1- дискриминационная характеристика (2), 2 – сумма дискриминационной и флюктуационной характеристик.
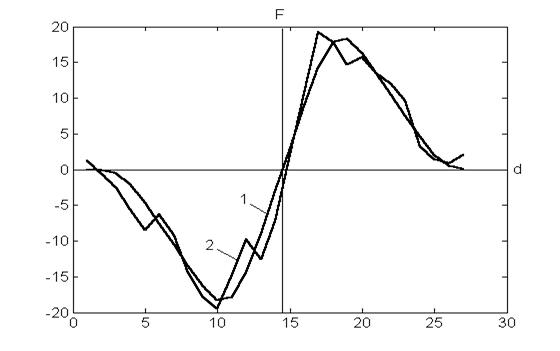
Рис. 5. Реализация дискриминационной характеристики, 
Время прихода оценивается как момент пересечения реализацией нулевого уровня: находится номер отсчета  , когда впервые ее значение больше нуля. Время прихода кладется равным
, когда впервые ее значение больше нуля. Время прихода кладется равным
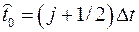 :
:
к  добавляется
добавляется  , так как время отсчитываеся с нуля, а счетчик цикла в MATLAB – с единицы.
, так как время отсчитываеся с нуля, а счетчик цикла в MATLAB – с единицы.
Результаты моделирования по массиву реализаций дискриминационной характеристики размерностью 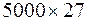 приведены в табл. 1.
приведены в табл. 1.
Табл. 1
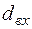
| ||||||
 
| 14.167 | 14.475 | 14.506 | 14.503 | 14.499 | 14.500 |
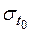
| 1.022 | 0.511 | 0.341 | 0.204 | 0.146 | 0.102 |
 
| 1.724 | 0.694 | 0.500 | 0.225 | 0.080 | 0.000 |
 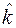
| 1.997 | 3.994 | 5.992 | 9.986 | 13.980 | 19.972 |
Задание
Индивидуальное задание формулирует преподаватель, комбинируя сигналы и шум:
|
|
|
1.  ,
,
2. 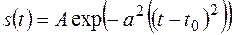 ,
,
3. 
4. сигнал прямоугольной формы длительностью  ;
;
1.  ,
,
2.  ,
,
3.  ,
,
4.  .
.
Список литературы
1. Воробьев С.Н., Осипов Л.А. Моделирование систем. – СПб.: ГУАП, 2005. –
66 с.
2. Тихонов В.И. Нелинейные преобразования случайных процессов. - М.:
Радио и связь, 1986. – 296 с.
3. Воробьев С.Н., Гирина Н.В., Лазарев И.В., Осипов Л.А. Статистическое мо-
делирование информационных систем, часть 1. Учебн. Пособие. – СПб.:
ГУАП, 2010. - 152 с.
Лабораторная работа № 7
|
|
|


