 |
Модуляция и демодуляция в пакетах
|
|
|
|
SIGNAL PROCESSING, COMMUNICATIONS
1. Модуляция в пакете SIGNAL PROCESSING
В пакете SIGNAL PROCESSING системы MATLAB [1,2] имеются универсальные функции расчета модулированного и демодулированного сигналов
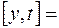modulate 
, (1)
demod 
, (2)
где 
- вектор отсчетов модулирующего сигнала 
, 
- несущая частота, 
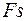- частота дискретизации, 
- вид модуляции, 
- дополнительный (необязательный) параметр. Вектор моментов времени задается следующим образом:
.
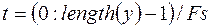При амплитудной модуляции (АМ) параметр имеет значение 
: здесь 
- АМ, 
- две боковые полосы, 
- передача несущей. Функция модуляции (1) записывается
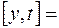modulate 
,
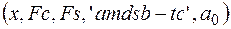параметр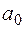 
задает уровень несущей. АМ – сигнал
.
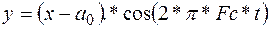Если модулирующий сигнал является двуполярным, задается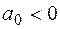 
. По умолчанию 
, что обеспечивает однополярность множителя 
. Функция (2)
demod 
.
Частотная и фазовая модуляция обозначаются ‘fm’, ‘pm’.
В [3] приведены следующие примеры программирования систем АМ –, ЧМ-, ФМ – модуляции и демодуляции.
Пример 1. Амплитудная модуляция прямоугольного сигнала (рис. 1) длительностью 
с, частота несущей 
Гц, частота дискретизации 
Гц; АМ сигнала 
, частота несущей 
Гц, частота дискретизации Гц.
На рис. 1 показаны: 1 – модулирующий сигнал; 2 – огибающая АМ – сигнала;
3 – АМ – сигнал.
Рис. 1. АМ – сигналы
Пример 2. Частотная модуляция сигналов из примера 1 (рис. 2). Несущие частоты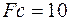 
Гц, 
Гц; частоты дискретизации 
Гц, Гц.
На рис. 2 показаны ЧМ – сигналы: 1 – модулирующие сигналы, 3 – модулированные сигналы.
Рис. 2. ЧМ – сигналы
На рис. 3 жирными линиями показаны демодулированные сигналы.
Рис. 3. Демодулированные ЧМ – сигналы
Пример 3. Фазовая модуляция (ФМ) сигналов из примера 1. Несущие частоты 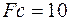Гц, Гц; частоты дискретизации Гц, Гц.
|
|
|
На рис. 4 показаны ФМ – сигналы, на рис. 5 – демодулированные ФМ – сигналы.
Рис. 4. ФМ – сигналы
Рис. 5. Демодулированные ФМ – сигналы
2. Манипуляция в пакете COMMUNICATIONS
Универсальные функции
dmod 
,
ddemod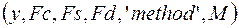 
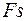задают манипуляцию и деманипуляцию, имитирующие передачу цифровых сигналов. Параметры: - несущая частота, - частота дискретизации, отношение 
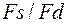равно числу отсчетов на один сигнал 
, 
- число уровней манипуляции. Параметр : 
- амплитудная, 
- частотная, 
- фазовая манипуляция.
Пример 4. Передается последовательность сигналов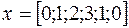 
амплитудной манипуляцией с 
уровнями (рис. 6).
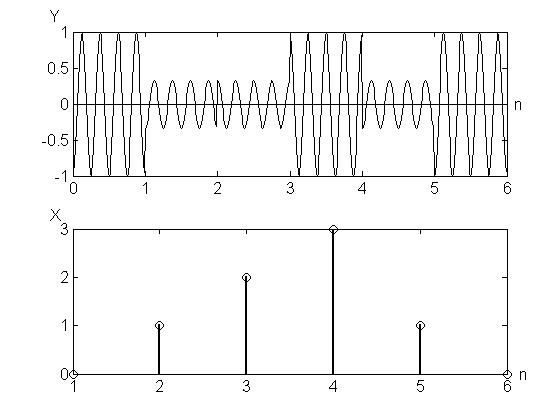
Рис. 6. Амплитудная манипуляция
Пример 5. Те же сигналы передаются с помощью частотной манипуляции
(рис. 7).
Рис. 7. Частотная манипуляция
Пример 6. В программе фазовой манипуляции (рис.8) изменяются операторы
Рис. 8. Фазовая манипуляция
Задание
1. Сравнить виды модуляции по помехоустойчивости. Для этого к сигналу следует добавить случайную составляющую – шум, генерируемый функцией RANDN. Например, если задать передаваемый сигнал суммой
si=0.3 % с.к.о. шума
x=rectpuls((t-30),25)+si*randn(1,n);
то частотная модуляция прямоугольного и косинусоидального сигналов описывается, наприер, программой
Fc=10
Fs=80
n=5000
t=0: 1/Fs: (n-1)/Fs;
x=rectpuls((t-30),25)+0.3*randn(1,n);
[y,t]=modulate(x,Fc,Fs,'fm'); % модулированный прямоугольный
сигнал
subplot(1,2,1),plot(t,y,t,x,'r')
Fc1=5
Fs1=100
t1=0:0.02:2;
n1=length(t1)
x1=cos(2*pi*t1)+0.3*randn(1,n1); % модулированный косинусоидальный
сигнал
[y1,t1]=modulate(x1,Fc1,Fs1,'fm');
subplot(1,2,2),plot(t1,y1,t1,x1,'r')
pause
X=demod(y,Fc,Fs,'fm'); % демодулированный прямоугольный
сигнал
subplot(1,2,1),plot(t,X,t,x,'r')
X1=demod(y1,Fc1,Fs1,'fm'); % демодулированный косинусоидальный
сигнал
subplot(1,2,2),plot(t1,X1,t1,x1,'r')
Будут наблюдаться следующие осциллограммы: на рис 9 кривые 1 – исходные сигналы, кривые 2 – модулированные; на рис. 10 кривые 1 – исходные сигналы, кривые 2 – демодулированные.
|
|
|
Рис. 9. ЧМ - сигналы
Рис. 10. Сигналы
Способ сравнения помехоустойчивости изобретите сами.
2. Реализовать манипуляцию в соответствии с двоичным кодом, заданным преподавателем.
Контрольные вопросы
1. Какие существуют разновидности АМ? Ответ см. в [1].
2. Как демодулируется АМ – сигнал?
3. Применяются ли ФНЧ при демодуляции АМ – сигнала?
4. Связаны ли ЧМ – и ФМ – сигналы?
5. Каково назначение параметра в функциях (1) и (2)?
6. Каким образом кодируются четыре уровня сигнала при амплитудной манипуляции (рис. 6)?
Список литературы
1. Солонина А.И. и др. Основы цифровой обработки сигналов. - СПб.: БХВ,
2005. – 768 с.
2. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображе-
ний. - СПб.: Питер, 2002. – 608 с.
3. Воробьев С.Н., Осипов Л.А. Моделирование систем. СПб.: ГУАП, 2005. – 66 с.
|
|
|
