Несимметричные трехфазные системы

Если хотя бы одно из условий симметрии не выполняется, трехфазная цепь работает в несимметричном режиме. Такие режимы при подключении статической нагрузки рассчитываются любым из известных методов расчета линейных электрических цепей с источниками гармонических воздействий. Как правило, падением напряжения на внутреннем сопротивлении генератора пренебрегают и фазные напряжения генератора заменяются соответствующими идеальными источниками ЭДС. Поскольку в трехфазных цепях, помимо значений токов, обычно представляют интерес также величины потенциалов узлов, в большинстве случаев для расчета применяется метод узловых потенциалов.

Если заданны линейные напряжения, удобно рассчитывать трехфазные цепи при соединении фаз нагрузки в треугольни к. Пусть в схеме (см. рис. 1, б) нагрузка несимметрична и . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома фазные токи

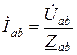; ; . (11)

По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:

. (12)

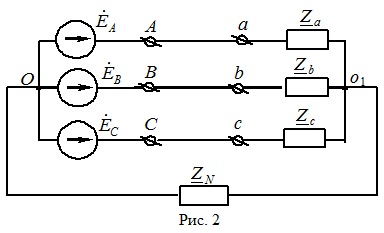
Если к трехфазному генератору, фазы которого соединены звездой (рис. 2), подключен приемник электрической энергии, фазы которого также соединены звездой, то в случае несимметричной трехфазной системы между нейтральными (нулевыми) точками приемника и генератора возникает напряжение смещения нейтрали

, (13)

здесь – комплексы ЭДС соответствующих фаз генератора; – комплексные проводимости соответствующих фаз нагрузки и нейтрального (нулевого) провода.

Напряжение на фазах нагрузки

(14)

Токи в фазах

(15)

Ток нейтрального провода

. (16)

При расчете трехфазной системы «звезда – звезда с нейтральным проводом с сопротивлением 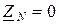» нет необходимости рассчитывать напряжение смещения нейтрали, поскольку . В этом случае трехфазную систему можно рассматривать как совокупность трех независимых контуров и рассчитывать каждый контур известными методами расчета цепей синусоидального тока. Целесообразно использовать векторные диаграммы при расчете таких цепей.

В случае отсутствия нейтрального провода в формуле (13) проводимость нейтрального провода принимают равной нулю. При этом, если генератор симметричный, а симметрия нагрузки нарушена сопротивлением нагрузки, подключенном в одной из фаз (например, ), удобно для определения напряжения смещения нейтрали воспользоваться формулой:

, (17)

для оставшихся случаев и соответственно

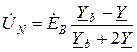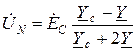; . (18)

Если нагрузка соединена звездой без нейтрального провода и известны линейные напряжения , то фазные напряжения нагрузки находятся по формулам:

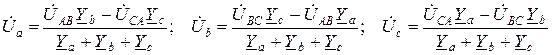. (19)

Для любой трехфазной системы сумма комплексных значений линейных напряжений равна нулю:

. (20)

ЗАДАНИЕ

1. По заданному номеру варианта изобразить цепь, подлежащую расчету, выписать значения параметров элементов цепи.

2. Рассчитать фазное и линейное напряжение генератора, ток, фазное и линейное напряжения нагрузки, мощность, вырабатываемую генератором и расходуемую в нагрузке в симметричном режиме.

3. Рассчитать потенциалы всех точек и построить совмещенную топографическую диаграмму потенциалов, принимая потенциал нейтральной точки генератора равным нулю, и векторную диаграмму токов для симметричного режима.

5. Определить аналитически и по топографической диаграмме напряжение между двумя заданными точками, записать мгновенное значение этого напряжения.

7. Составить уравнение баланса активных и реактивных мощностей генератора и нагрузки, проверить его выполнимость для симметричного режима.

Выбор варианта и параметров элементов цепи

1. По заданному номеру варианта изобразить цепь (рис. 3), подлежащую расчету, выписать значения параметров элементов.

2. В качестве источника задан симметричный трехфазный генератор, обмотки которого соединены звездой с прямой последовательностью чередования фаз. Величина ЭДС фазы А для четных вариантов выбирается равной 127 В, для нечетных вариантов – 220 В. Численные значения комплексных сопротивлений обмоток генератора в Омах рассчитываются по следующей формуле:

,

где − сумма цифр номера варианта;

− разность цифр номера варианта (из первой цифры вычитается вторая; если число – однозначное, то равно номеру варианта).

Например, для варианта № 35 комплексное сопротивление обмоток генератора

Ом,

для варианта № 53

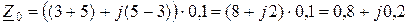Ом,

для варианта № 88

Ом.

3. Граф схемы, режим нейтрали, несимметричный режим и определяемое напряжение заданы в таблице 1.

4. Численные значения комплексных сопротивлений линии определяются по формуле:

где B ₁ – первая цифра номера варианта (если число – однозначное, то 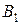равно номеру варианта).

5. Численные значения комплексных сопротивлений фазы определяются по формуле:

Табл. 1

вариант	граф	, Ом	напряжение
1, 34, 67	а		unf
2, 35, 68	б	−	umf
3, 36, 69	а		ube
4, 37, 70	б	−	ued
5, 38, 71	а	∞	umk
6, 39, 72	б	−	umd
7, 40, 73	а		umn
8, 41, 74	б	−	ued
9, 42, 75	а		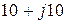uAb
10, 43, 76	б	−	uAf
11, 44, 77	а		uOn
12, 45, 78	б	−	ueA
13, 46, 79	а		uAe
14, 47, 80	б	−	uak
15, 48, 81	а		unk
16, 49, 82	б	−	umf
17, 50, 83	а		ube
18, 51, 84	б	−	uae
19, 52, 85	а	∞	umb
20, 53, 86	б	−	uak
21, 54, 87	а		udc
22, 55, 88	б	−	ucd
23, 56, 89	а		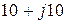ume
24, 57, 90	б	−	udn
25, 58, 91	а		umd
26, 59, 92	б	−	uAk
27, 60, 93	а		ueA
28, 61, 94	б	−	udn
29, 62, 95	а		umk
30, 63, 96	б	−	uBd
31, 64, 97	а	∞	umf
32, 65, 98	б	−	ume
33, 66, 99	а		uOk

ПРИМЕР РАСЧЕТА

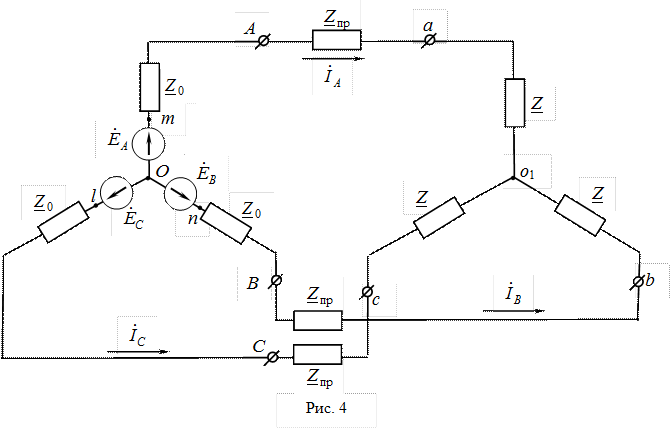Дано: к симметричному трехфазному генератору (рис. 4) с фазной ЭДС E = 220 В и внутренним сопротивлением Ом через линию, сопротивление каждого провода которой Ом, подключена симметричная нагрузка 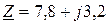Ом, соединенная звездой.

Решение. Запишем фазные ЭДС генератора в комплексном виде:

В; В;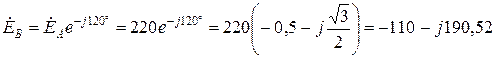

В.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: