 |
Дробные выражения имеют смысл только в том случае, если выбранные значения не обращают в нуль знаменатель выражения: вспомним наше «золотое правило» – на нуль делить нельзя.
|
|
|
|
Иррациональное выражение не будет иметь смысл при значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени.
Множества в математике.
В математике широко используется понятие множество.
Вообще множество – совокупность предметов. При этом предполагается, что предметы рассматриваемой совокупности отличаются друг от друга и от предметов, не входящих в нее. Отдельный предмет совокупности – элементмножества. Множества обычно обозначают большими буквами латинского алфавита (А, В, С, … Х, …)
Если элементами множества являются числа, то говорят о числовом множестве.
Для графического представления числовых множеств пользуются координатнойпрямой.
Координатная прямая это любая прямая, на которой выбрано направление, принимаемое за положительное, точка – начало отсчета, единица измерения – масштабный отрезок, длина которого принимается равной единице.
Любая точка координатной прямой – изображение какого-либо числа.
Иными словами, координата точки однозначно задает эту точку на координатной прямой.
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Координату точки записывают в круглых скобках справа от буквы, которой обозначена точка. Например, если точка М имеет координату x, то можно записать М (x)
При этом число x, будет равно по величине длине отрезка 0М, со знаком «
», если точка М находится справа от начала отсчета, или со знаком «–», если М расположена слева от точки 0.
Простейшие числовые множества называют числовымипромежутками. Числовые промежутки в зависимости от их конфигурации называются по-разному и имеют различное графическое представление на числовой прямой
|
|
|
отрезок 
| |||
интервал 
| 
| ||
промежуток открытый слева 
| 
| ||
промежуток открытый справа 
| 
| ||
числовой луч 
| 
| ||
открытый числовой луч 
| 
| ||
| Отдельные точки числовой прямой, не входящие в область допустимых значений, принято называть «выколотыми» и изображать, как это показано слева. На рисунке выколотой является точка a | ||
Функции в математике.
Рассмотрим выражение 
. В нем есть одна переменная величина – это 
. Предположим, что все возможные значения этой переменной являются элементами числового множества X. Для каждого значения можно определить числовое значение этого выражения. Обозначим его 
и запишем 
. Можно сделать очевидный вывод, что для любого элемента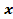 
множества X существует число , которое определяется как числовое значение выражения. Эти числовые значения можно рассматривать как элементы числового множества Y.
Но если каждому элементу числового множества X поставлено в соответствие действительное число, то считается, что на множестве X определена числовая функция.
При этом множество X называется областьюопределения функции. Произвольный элемент области определения (обычно обозначается буквой х) называется аргументом функции или независимойпеременной. Множество Y всех значений y называется множеством значений функции.
Можно сказать, что функция – отображение одного подмножества (области определения) на другое подмножество (множествозначений) множества действительных чисел.
В рассмотренном примере функция задана формулой. В общем виде функцию одного переменного в случае задания формулой записывается так: 
где выражение 
определяет последовательность математических операций, которые надо выполнить над аргументом, чтобы получить значение функции.
|
|
|
Такой способ задания функции называют аналитическим
Выражение – формула функции. В рассматриваемом примере формула не является дробью и не содержит элементов иррациональности. Поэтому значением аргумента x может быть любое действительное число.
Но в общем случае следует учитывать, что функция будет определена на множестве тех значений аргумента, для которых указанные в формуле действия выполнимы.
Множество всех таких значений аргумента называется естественнойобластьюопределения.
|
|
|
