 |
Во всех случаях, когда функция задается формулой, возникает задача нахождения области определения (имеется в виду естественной области определения) функции.
|
|
|
|
Графики функций.
Очень распространенным способом задания функций является графический способ.
Графикфункции даёт о ней наглядное представление. Если упоминавшиеся выше множества X и Y (область определения и множество значений) являются множествами действительных чисел, тографик функции совокупность точек на координатной плоскости.
Обычно для построения графика функции используют прямоугольную систему координат. Перед тем как приступить к построению графика необходимо подготовить пары чисел (x,y), каждая из которых будет определять положение соответствующей точки на координатной плоскости. При этом значение x будет выбираться произвольно, а значения y подсчитываться по формуле. 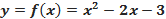
Количество необходимых для построения графика точек определяется исходя из стоящих задач:
- получить наглядное представление о графике на определенном участке;
- получить общее представление о графике в целом;
- максимально подробно передать характер поведения функции на определенном участке;
Наиболее удобной формой представления полученного в ходе подготовки к построению графика числового материала является таблица значений. Такая таблица представляет еще один способ задания функции – табличный.
Приведенная ниже таблица позволяет нанести на координатную плоскость точки, заданные соответствующими парами чисел и, соединив их плавной линией, получить график.
| x | -2 | -1 | |||||
| y | -3 | -4 | -3 |

Особого внимания заслуживают точки графика с координатами (-1, 0) и (3, 0).
В этих точках функция имеет нулевые значения. Такие точки приято называть нулями функции. Определить нули функции это значит найти те значения аргумента x, при которых
|
|
|

Выражение вида  это равенство, о чем говорилось ранее. При наличии в выражении неизвестного равенство принято называть уравнением.
это равенство, о чем говорилось ранее. При наличии в выражении неизвестного равенство принято называть уравнением.
Найти значения неизвестного, при которых равенство будет верным, значит решить уравнение или найти его корни.
Если в точке нуля функции график пересекает ось абсцисс, то сама функция меняет знак.
Три способа задания функции, упомянутые выше (аналитический, табличный, графический), не исключают, а лишь дополняют друг друга.
Неравенства.
Если сделать запись, состоящую из двух выражений, но связать их не знаком равенства, а одним из следующих знаков « », то мы получим неравенство. Неравенства также как равенства могут быть числовыми и алгебраическими. Наиболее простыми являются неравенства, содержащие одно переменное в первой степени. Такие неравенства принято называть линейными.
», то мы получим неравенство. Неравенства также как равенства могут быть числовыми и алгебраическими. Наиболее простыми являются неравенства, содержащие одно переменное в первой степени. Такие неравенства принято называть линейными.
Например, 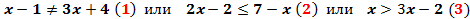
Начиная решать линейное неравенство, следует выполнить тождественные преобразования, в ходе которых все элементы (члены), содержащие переменную, окажутся в левой части неравенства, а остальные – в его правой части:
Пример 1. Выполняя преобразования, получим:
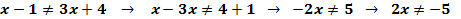
Решить такое неравенство очень просто. Надо найти значение переменной, обращающее выражение в верное равенство, и исключить это значение.
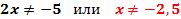
Пример 2. Выполняя преобразования, получим:
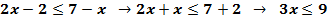
Его решение приведет нас к следующему результату: 
Пример 3. Выполняя преобразования, получим:
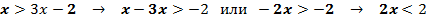
В последнем переходе, мы домножили обе части неравенства на (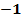 ). При этом сменился и знак неравенства с (
). При этом сменился и знак неравенства с ( ) на (
) на ( ).
).
Завершая решение, получим: 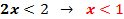
Результаты можно представить графически, воспользовавшись числовой осью

| В первом случае решением неравенства будет любое действительное значение переменной x кроме х = 2,5. Точка М «выколота». |

| Во втором случае областью решений неравенства будет числовой луч
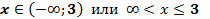
|

| Во третьем случае областью решений неравенства будет открытый числовой луч
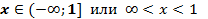
|
Если переменная входит в неравенство не только в первой, но и во второй степени, то перед нами квадратное неравенство. Решение простейшего целого квадратного неравенства сводится к выполнению определенного алгоритма.
|
|
|
На первом этапе выполняется ряд тождественных преобразований (по аналогии с линейными неравенствами), чтобы привести исходное неравенство к виду:

Если оно имеет такой вид изначально, то этот этап пропускается.
Квадратные неравенства можно решать двумя способами. Один способ – это метод интервалов. Годится для решения любых неравенств вообще. Здесь же мы разберём более простой способ – графический. Способ прост, нагляден и не требует особых расчётов.
Если вспомнить, что выражение  это формулаквадратичной функции, графиком которой является парабола, то можно, используя свойства графика, найти решение любого неравенства такого вида вне зависимости от конкретных значений коэффициентов a, b, c, не прибегая при этом к громоздким аналитическим выкладкам.
это формулаквадратичной функции, графиком которой является парабола, то можно, используя свойства графика, найти решение любого неравенства такого вида вне зависимости от конкретных значений коэффициентов a, b, c, не прибегая при этом к громоздким аналитическим выкладкам.
Для такого решения достаточно выяснить наличие нулей функции 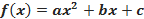 (выяснить, есть ли корни у уравнения
(выяснить, есть ли корни у уравнения  ) При этом следует учесть знак коэффициента a (
) При этом следует учесть знак коэффициента a (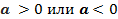 ).
).
Совершенно очевидно, что возможное количество вариантов невелико:
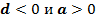




Рассмотрим эти варианты
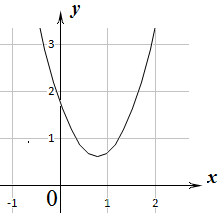
| 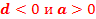 Поскольку дискриминант отрицателен, уравнение
Поскольку дискриминант отрицателен, уравнение  действительных корней не имеет.
График функции действительных корней не имеет.
График функции 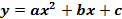 не пересекает ось х и располагается в положительной полуплоскости (в I и II четвертях системы координат). Ветви параболы будут направлены «вверх».
В этом случае выражение не пересекает ось х и располагается в положительной полуплоскости (в I и II четвертях системы координат). Ветви параболы будут направлены «вверх».
В этом случае выражение  будет тождественно положительным и исходное неравенство будет тождественно положительным и исходное неравенство  в таком случае будет тождественным. Тождественным принято называется неравенство, которое оказывается верным при любом значении входящего в него переменного. в таком случае будет тождественным. Тождественным принято называется неравенство, которое оказывается верным при любом значении входящего в него переменного.
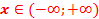
|
| 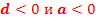 Поскольку дискриминант отрицателен, уравнение
Поскольку дискриминант отрицателен, уравнение  действительных корней не имеет.
График функции действительных корней не имеет.
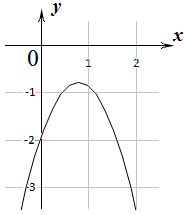
График функции 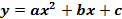 не пересекает ось х но располагается в отличие от предыдущего примера, в отрицательной полуплоскости (в III и IV четвертях системы координат). Ветви параболы будут направлены «вниз».
В этом случае выражение не пересекает ось х но располагается в отличие от предыдущего примера, в отрицательной полуплоскости (в III и IV четвертях системы координат). Ветви параболы будут направлены «вниз».
В этом случае выражение  будет тождественно отрицательным. Исходное неравенство будет тождественно отрицательным. Исходное неравенство  в таком случае вообще не будет иметь решения. в таком случае вообще не будет иметь решения.
|

|  Поскольку дискриминант равен нулю, уравнение
Поскольку дискриминант равен нулю, уравнение  имеет два равных действительных корня..
График функции имеет два равных действительных корня..
График функции 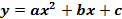 касается оси в точке х и располагается в положительной полуплоскости (в I и II четвертях системы координат). Ветви параболы будут направлены «вверх».
Неравенство касается оси в точке х и располагается в положительной полуплоскости (в I и II четвертях системы координат). Ветви параболы будут направлены «вверх».
Неравенство  в таком случае будет вернымпри любом значении аргумента, кроме х. в таком случае будет вернымпри любом значении аргумента, кроме х.

|
|
|
|
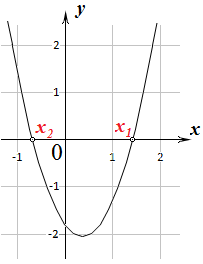
|  Поскольку дискриминант положителен, уравнение
Поскольку дискриминант положителен, уравнение  имеет два действительных корня имеет два действительных корня  и и 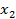 .
График функции .
График функции 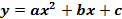 пересекает ось х в этих точках. При этом ветви параболы располагаются в положительной полуплоскости (в I и II четвертях системы координат) и направлены «вверх», а «основание» параболы расположено в отрицательной полуплоскости (в III и IV четвертях системы координат).
В этом случае неравенство пересекает ось х в этих точках. При этом ветви параболы располагаются в положительной полуплоскости (в I и II четвертях системы координат) и направлены «вверх», а «основание» параболы расположено в отрицательной полуплоскости (в III и IV четвертях системы координат).
В этом случае неравенство  будет верно в случае будет верно в случае

 На координатной оси решение можно представить в виде такого рисунка:
Можно представит словесный вариант. Произвольно выбранное значение аргумента х будет решением неравенства На координатной оси решение можно представить в виде такого рисунка:
Можно представит словесный вариант. Произвольно выбранное значение аргумента х будет решением неравенства
 если будет выполнено одно из условий:
если будет выполнено одно из условий:
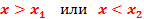 . .
|
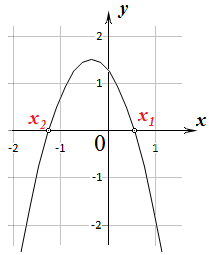
|  Поскольку дискриминант положителен, уравнение
Поскольку дискриминант положителен, уравнение  имеет два действительных корня имеет два действительных корня 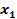 и и  .
График функции .
График функции 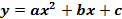 пересекает ось х в этих точках. При этом ветви параболы располагаются в отрицательной полуплоскости (в III и IV четвертях системы координат) и направлены «вниз», а «основание» параболы расположено в положительной полуплоскости (в I и II четвертях системы координат).
В этом случае неравенство пересекает ось х в этих точках. При этом ветви параболы располагаются в отрицательной полуплоскости (в III и IV четвертях системы координат) и направлены «вниз», а «основание» параболы расположено в положительной полуплоскости (в I и II четвертях системы координат).
В этом случае неравенство  будет верно в случае будет верно в случае

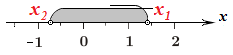 На координатной оси решение можно представить в виде такого рисунка:
Можно представит словесный вариант. Произвольно выбранное значение аргумента х будет решением неравенства На координатной оси решение можно представить в виде такого рисунка:
Можно представит словесный вариант. Произвольно выбранное значение аргумента х будет решением неравенства
 если будут одновременно выполнены два условия:
если будут одновременно выполнены два условия:
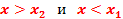 . .
|
Используя представленные выше рассуждения решим квадратное неравенство:
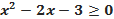
Это неравенство уже готово для решения. Слева – квадратный трёхчлен, справа – ноль.
Записываем и решаем уравнение:

Определяем дискриминант
|
|
|
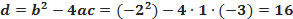
Поскольку дискриминант положителен, находим корни уравнения:

Поскольку в рассматриваемом примере  , обратимся к четвертому варианту.
, обратимся к четвертому варианту.
|
|
|


