 |
Методика определения давления селевых потоков и паводков на откос дороги
|
|
|
|
Решением задачи взаимодействия, селевого потока с инженерными сооружениями (земляным полотном дорог) занимаются различные институты как в нашей стране, так и за рубежом. Однако до сих пор отсутствуют достаточно надежные теоретические и экспериментальные расчетные зависимости, вскрывающие механизм соударения селевого потока с инженерными сооружениями. Сложность решения вопроса, помимо других многочисленных причин, заключается еще и в том, что взаимодействие селевого потока с земляным полотном зависит также от вида селевого потока, формирующегося в данном селеносном бассейне.
Проводятся обширные исследования динамики селевых потоков, однако пока еще нет общепризнанных зависимостей, описывающее движение селя, которые могут быть подтверждены в натурных условиях. Это вызвано сложностью физико-механической и динамической структуры селевых потоков, не подчиняющихся обычным законам гидродинамики, трудностями моделирования этих потоков в лабораторных условиях (необходимостью создания специального оборудования), высокими концентрациями массы и связанными с этим сложностями ее циркуляции на экспериментальных установках и др.
Указанные обстоятельства значительно препятствуют экспериментальному изучению природы селевых потоков, установлению их точных динамических характеристик и изучению схемы взаимодействия потока и препятствий.
Одним из основных вопросов при рассмотрении нагрузки от селевых потоков является установление концепции о характере их движения [ 46, 47, 48]. В настоящее время существуют две точки зрения. Согласно первой, основным видом движения селевых потоков, в том числе и потоков, обладающих вязкопластическими свойствами, является течение в турбулентном режиме при минимальном влиянии сил вязкости на кинематику и динамику потока [ 47, 48]. Принятие ее дало возможность на первом этапе использовать для исследования и описания динамики селевого потока метода гидравлики и гидродинамики.
|
|
|
Согласно второй точке зрения, предполагается наличие существования структурного режима движения селевого потока (по мнению автора, такие потоки имеют ограниченные возможности существования). Вопросам динамики структурных потоков посвящены также работы [ 48- 52]. Нагрузки от движения структурного слоя в однородной массе, несмотря на большие коэффициенты сопротивления, ввиду малых скоростей движения не превышают нагрузки от потоков, текущих в турбулентном режиме [ 53]. Большие скорости могут быть лишь на коротких участках с крутыми уклонами, где происходит, скольжение массы по подстилающей поверхности. В последнем случае воздействие массы должно, скорее всего, описываться зависимостями для неупругого удара твердых тел.
Проведение специальных методических исследований по изучению вопросов силового воздействия селевых потоков, текущих в различных режимах, и по установлению реальных расчетных схем воздействия в дальнейшем позволит разработать более точные методы расчета, снять излишние запасы прочности проектируемых инженерных сооружений, повысить надежность их работы. В процессе таких исследований выявится возможность более полного использования относительно богатого материала по воздействию на сооружение морских волн и снежных лавин,
В настоящее время почти полностью отсутствуют экспериментальные материалы, реально отражающие специфические особенности динамики многофазного селевого потока.
Среди различных подходов к решению проблемы динамического воздействия потока на вертикальные преграды наибольшее распространение получили методы, в которых динамическое давление представляется давлением струи воды на плоскую преграду, которое выражается формулой
|
|
|
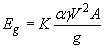(3)
где К - коэффициент, определяемый экспериментальным путем;
a - корректив скорости;
g - удельный вес потока;
А - площадь струи;
V - скорость потока.
Формула (3) выведена с применением теоремы импульсов в предположении, что воздействие перешло в давление обтекания и что расход потока за период воздействия остается постоянным; силы трения преграды не учитываются.
Для решения поставленной задачи необходимо располагать данными о форме фронта потока, распределении скоростей на фронте волны, а также о распределении во времени всех этих параметров с учетом влияния твердой фазы в потоке, формы и упругих свойств преграды и и.п.
Расчет параметров неустановившегося движения селевого потока сам по себе представляет сложную задачу, рассмотренную в работе [ 54].
Однако можно с достаточным основанием использовать для определения динамической составляющей давления простые зависимости формулы (3), основанные на применении теоремы импульсов к развитому давлению для установившегося потока с постоянными расходом и массой.
Форма живого сечения русла на подходе к сооружению, а также размеры и формы самого сооружения в пределах ширины русла изменяются иногда значительно. Для облегчения расчетов русло по ширине всегда можно разбить на ряд характерных участков, в пределах которых все расчетные параметры могут быть определены для одной вертикали.
В результате экспериментальных исследований, проведенных в ЗакНИГМИ [ 55], по воздействию на преграды глинистого раствора сделан вывод о том, что в начальный момент подхода потока к сооружениям на датчиках давления не было зафиксировано каких-либо значительных скачков давления, превышающих давление установившегося потока. Для гарантии рассредоточения ударного давления во времени можно рекомендовать придавать передним граням земляного полотна уклон более 1:5.
д ля упрощения расчета, принимают допущения, что расход и скорости течения в рассматриваемый промежуток времени остаются постоянными.
Г.М. Беручашвили рассматривает схему, по которой возможен как перелив потока через преграду V 2 = 0, так и обрушение его на верхний бьеф (рис. 47).
|
|
|
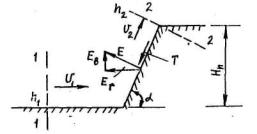
Рис. 47. Расчетная схема откоса для определения давления селевых потоков
На основании этой схемы уравнения импульсов между сечениями 1-1 и 2-2 в горизонтальной (г) и вертикальной (в) проекциях имеют вид:
Е г = Е · sin a = m·V1 +P1 – (m·V2 + P2 + T) cos a
Ев = E·cos a = Ro б + (m·V2 + P2 + T) sin a (4)
где Е - полное давление;
P1, P2 - силы гидростатического давления в сечениях 1-1 и 2-2, равные
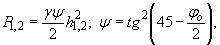(5)
где j о - угол естественного откоса селевой массы;
g - плотность селевого потока;
Т - сила трения потока о наклонную грань;
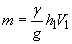- масса потока, проходящего в единицу времени в сечении 1-1;
V 1, h 1 и V 2, h 2 - соответственно скорости и глубины потока в сечениях 1-1 и 2-2.
Масса потока, набежавшего на наклонную грань, определяется по формуле
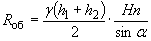(6)
или с учетом
V1· h1 = V2· h2
(7)
В результате подстановки выражение Беручашвили принимает вид
(8)
или
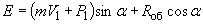(9)
На вертикальную стенку
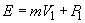
или после подстановки значений т и Р 1
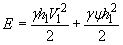(10)
При выводе формулы (8) члены, содержащие давление в створе 2-2 и трение, исключаются.
Введение в выражение статического давления, коэффициента, учитывающего угол внутреннего трения потока, представляется вполне обоснованным, хотя количественные данные требуют тщательного изучения (например Мостков М.А. предлагает принять j =16°, y = 0,57,а И.И. Херхеулидзе - j о = f (g c)т.е. j = 7.24(g - 1)5,82
Для определения V 2записывается уравнение Бернулли между сечениями 1-1 и 2-2.
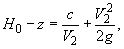(11)
где
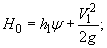
Hn - высота плотины; i - уклон;
(12)
Скорость V 2рекомендуется определять из уравнения подбором. В работе [ 56] приведена следующая запись исходного уравнения импульсов в проекции на горизонтальную ось:
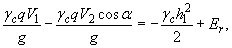
откуда
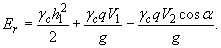(13)
С учетом постоянства расхода
q = V 1 h 1 = V2 h2
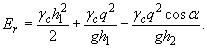(14)
Уравнение Бернулли
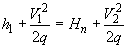(15)
откуда
(16)
Горизонтальная проекция силы полного давления определяется по формуле
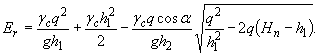(17)
В этих выводах принято, что P 2= Т =0и R об= 0.
Максимум суммарного давления определяется анализом при переменной V или h формулы (10), который приводит к следующим связям
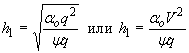(18)
где a o - коэффициент Буссинеска (корректив скорости по количеству движения).
|
|
|
Этот критерий дает возможность оценить по глубине потока, на каких участках русла может снижаться или увеличиваться давление.
Если в формуле (17) принять h = Hn и ввести корректив скорости по количеству движения, то получим формулу
(19)
Принято
h1 = hc, V1 = Vc
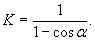
В исходную формулу необходимо ввести расчетную формулу скорости с учетом корректирующего члена, учитывающего влияние твердой фазы. По И.И. Херхеулидзе.
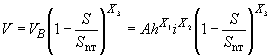(20)
где А - числовой коэффициент;
S - объемная концентрация наносов
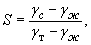(21)
где g c - плотность массы селевого потока;
g ж - плотность жидкой составляющей;
g т - плотность твердой составляющей;
S n т - предел текучести селевой масса
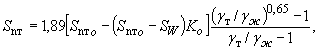(22)
где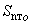 
- объемная концентрация на пределе текучести при отсутствии коллоидов;
SW - объемная концентрация при 100%-ном содержании коллоидов.
Последняя зависимость рекомендуется как наиболее простая и удобная для приближенных расчетов.
|
|
|
