Покажите, как изменяются давление и температура потока реального газа при дросселировании.

При дросселировании газа или пара протекает необратимый процесс снижения давления без совершения внешней работы. Если в канале имеется местное сопротивление в виде резкого сужения вида перегородки с отверстием, задвижки, клапана и т.п., то газовый поток перестраивает свою геометрическую форму, как до сужения, так и после него. Перестройка формы потока и перетекание через само сужение связано с образованием вихревых движений газа. Часть кинетической энергии потока идет на образование вихрей, часть – на преодоление сопротивления трения. Затраченная на это энергия необратимо превращается в теплоту, которая воспринимается газом. Поэтому давление после местного сопротивления не восстанавливается до первоначального. Изменение давления, скорости и температуры по длине канала приведено на рисунке. Скорость газа при протекании его через сужение возрастает, что вызывает снижение давления и температуры. После сужения скорость понижается, но давление, вследствие указанных причин, не восстанавливается до первоначального.

Степень снижения давления газа при дросселировании зависит от природы газа и его состояния, относительной величины сужения, скорости газа. Обозначим степень снижения давления через ; тогда ее величина будет равна:

,

где ∆р – величина снижения давления;

р – давление на входе в сужение.

В энергетических установках дросселирование нежелательно, т.к. при падении давления снижаются энергетические возможности газа. Но иногда дросселирование является необходимым и создается искусственно, например, в редукторах, регуляторах и т.п.

Изменение давления и температуры при дросселировании

При термодинамическом анализе особенностей процесса дросселирования целесообразно использовать общее уравнение энергии:

В канале можно обеспечить с₁ = с₂, тогда i₁ =i₂. Из чего следует, что энтальпия газа в процессе дросселирования остается постоянной.

Этот вывод справедлив как для идеальных, так и для реальных газов. При дросселирования идеального газа Т₁ = Т₂, поскольку i₁ = i₂. Это значит, что для идеального газа температура после дросселирования равна температуре на входе в дроссель.

Для реального газа изменение температуры при его дросселировании в отличие от идеального газа имеет своеобразный характер. Как показывают опыты, температура реального газа в результате дросселирования повышается, понижается или не изменяется. Это свойство впервые обнаружили ученые Д. Джоуль и У. Томсон, поэтому оно носит название э ф ф е к т а Д ж о у л я-Т о м с о н а.

Используя дифференциальные уравнения, связывающие i, s, ρ и T, можно получить для газа, подчиняющегося уравнению Ван-дер-Ваальса, следующую зависимость:

Отношение бесконечно малого изменения температуры к бесконечно малому изменению давления при дросселировании называется д р о с с е л ь - э ф ф е к т о м и обозначается

α =

Так как при дросселировании dp < 0, а c_p – величина положительная, то знак α будет зависеть от знака числителя выражения.

При этом возможны три случая:

а) < 0 (при T < ), тогда α > 0, т.е. dT < 0;

б) > 0 (при T > ), тогда α < 0, т.е. dT > 0;

в) = 0 (при T = ), тогда α = 0, т.е. dT = 0.

Изменение знака дроссель - эффекта α называется и н в е р с и е й,

а температура, при которой dT = 0, называется т е м п е р а т у о й и н в е р с и и и обозначается T_инв.

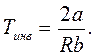
Каждый конкретный газ имеет индивидуальную температуру инверсии. Так, например, для воздуха Т_инв = 650 К; для водорода Т_инв = 204 К; для водяного пара Т_инв= 682 К.

Для установления температуры реального газа после дросселя необходимо сравнить T_вх с T_инв. Если температура газа на входе в дроссель равна его температуре инверсии, то после дросселя она восстановится до прежнего значения. При T_вх< T_инв температура газа после дросселя уменьшится, а при T_вх> T_инв - она возрастет.

Задача
1.14. В баллоне емкостью 40 л содержится азот при давлении р₁= 8 МПа и температуре t₁ = – 25 ⁰С. Определить количество теплоты, которое следует подвести к азоту, чтобы повысить его температуру до t₂ = 18 ⁰C. Каково будет конечное давление азота в баллоне?

Решение:

Конечное давление азота в баллоне:

P₂ = P₁*T₂/T₁ = 8*(18+273)/(273-25) = 9,4 МПа.

Массу азота в баллоне определяем из уравнения состояния:

P₁*V = m*R*T₁ → m = P₁*V/(R*T₁),

R = 297Дж/(кгК) – газовая постоянная для азота,

m = 8*10⁶*40*10^-3/(297*(273 – 25)) = 4,34 кг.

Количество теплоты, подведённое к азоту:

Q = m*C_vm*(t₂ – t₁) = 4,34*0,744*(18 – (-25)) = 138,845 кДж,

где C_vm = 0,744кДж/(кгК) – удельная массовая теплоёмкость азота при постоянном объёме.