 |
Определители квадратных матриц
|
|
|
|
ЛИНЕЙНАЯ АЛГЕБРА
Тема 1.1. Елементи теорії матриць
Матрицы. Действия над матрицами
Определение 1.1. Матрицей размера  называется прямоугольная таблица из чисел, содержащая
называется прямоугольная таблица из чисел, содержащая 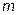 строк и
строк и  столбцов.
столбцов.
Согласно определению, общий вид матрицы размерности  представляется следующим образом:
представляется следующим образом:
 .
.
Числа 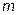 и
и  называются порядками матрицы. Числа
называются порядками матрицы. Числа  которые входят в матрицу, называются ее элементами. Индексы
которые входят в матрицу, называются ее элементами. Индексы  и
и  элемента
элемента  указывают соответственно на номера строки и столбца, в которых расположен элемент
указывают соответственно на номера строки и столбца, в которых расположен элемент  .
.
Часто матрицу записывают сокращенно в виде  , где
, где 
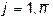 .
.
Определение 1.2. Матрица, все элементы которой равны нулю, называется нулевой.
Равенство матриц Сравнивить можно только матрицы одинаковой размерности
Определение 1.3. Две матрицы  и
и  называются равными, если они имеют одинаковые порядки, а соответствующие элементы равны между собой.
называются равными, если они имеют одинаковые порядки, а соответствующие элементы равны между собой.
Таким образом,  , если
, если  для всех значений
для всех значений 
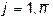 .
.
ОПЕРАЦИИ НАД МАТРИЦАМИ
- матрицы можно складывать (вычитать)
- матрицу можно умножить на число
- можно умножать матрицу на матрицу
Сложение и вычитание матриц
Складывать и вычитать можно только матрицы одной размерности
Определение 1.4. Суммой двух матриц 
 и
и 
 одних и тех же порядков
одних и тех же порядков 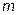 и
и  называется матрица
называется матрица 
 тех же порядков
тех же порядков 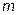 и
и  , элементы
, элементы  которой определяются равенством
которой определяются равенством  .
.
Итак, по определению

 .
.
Из определения суммы матриц следует, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно:
1) переместительным свойством:  ;
;
2) сочетательным свойством:  .
.
Эти свойства позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.
Умножение матрицы на число
|
|
|
Определение 1.5. Произведением матрицы  на вещественное число
на вещественное число  называется матрица
называется матрица  , элементы которой равны
, элементы которой равны

Умножение матриц
Определение 1.6. Произведением матрицы  имеющей порядки, соответственно равные
имеющей порядки, соответственно равные 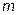 и
и  , на матрицу
, на матрицу  имеющей порядки соответственно равные
имеющей порядки соответственно равные  и
и  , называется матрица
, называется матрица  имеющая порядки соответственно
имеющая порядки соответственно 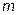 и
и  , элементы которой
, элементы которой  определены формулой
определены формулой
 (1. 1)
(1. 1)
Из приведенного определения следует, что матрицу  можно умножить на матрицу
можно умножить на матрицу  тогда и только тогда, когда число столбцов матрицы
тогда и только тогда, когда число столбцов матрицы  соответствует числу строк матрицы
соответствует числу строк матрицы  .
.
Формула (1.1) дает правило составления элементов матрицы 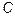 , являющейся произведением матрицы
, являющейся произведением матрицы  на матрицу
на матрицу  . Это правило называется правилом "строка на столбец" и может быть сформулировано следующим образом: элемент
. Это правило называется правилом "строка на столбец" и может быть сформулировано следующим образом: элемент  матрицы
матрицы  равен сумме попарных произведений соответствующих элементов
равен сумме попарных произведений соответствующих элементов  -й строки матрицы
-й строки матрицы  и
и  -го столбца матрицы
-го столбца матрицы  .
.
Задача 1.1. Определить  , если
, если  ,
, 

 .
.
Транспонирование матриц
Транспонированием матриц называется замена строк этой матрицы ее столбцами с сохранением их номеров. Матрица, полученная таким образом из матрицы  , называется транспонированной по отношению к матрице
, называется транспонированной по отношению к матрице  и обозначается
и обозначается  . Таким образом, если
. Таким образом, если  , то
, то 
Например, если  , то
, то 
Может оказаться, что квадратная матрица  совпадает со своей транспонированной матрицей, т.е.
совпадает со своей транспонированной матрицей, т.е.  или
или  . В таком случае матрица
. В таком случае матрица  называется симметричной.
называется симметричной.
Для операции трансформирования матриц характерны следующие свойства:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Квадратные матрицы
Если порядки матрицы 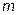 и
и  равны, то матрица называется квадратной, а число
равны, то матрица называется квадратной, а число  является ее порядком.В случае квадратной матрицы имеют
является ее порядком.В случае квадратной матрицы имеют
 .
.
Для квадратной матрицы вводят понятие главной и побочной диагоналей. Главной диагональю квадратной матрицы называется диагональ, идущая из левого верхнего угла в правый нижний ее угол. Побочной диагональю той же матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.
|
|
|
Определение 1.7. Квадратная матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной.
Определение 1.8. Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны единице, называется единичной и обозначается через  .
.
 .
.
С каждой квадратной матрицей связывают вполне определенную числовую характеристику, которая называется определителем, соответствующим этой матрице.
Тема 1.2. Определители
Определители квадратных матриц
Рассмотрим произвольную квадратную матрицу порядка  .
.

Определителем (детерминантом) квадратной матрицы  является число, которое обозначается
является число, которое обозначается  или
или  , или
, или  . В связи с отмеченным нельзя отождествлять понятие матрицы и ее определителя.
. В связи с отмеченным нельзя отождествлять понятие матрицы и ее определителя.
Определение 1.9. Определителем, соответствующим квадратной матрице  -го порядка называется число, полученное из элементов такой матрицы по следующим правилам:
-го порядка называется число, полученное из элементов такой матрицы по следующим правилам:
1) определитель  -го порядка равен алгебраической сумме
-го порядка равен алгебраической сумме  элементов;
элементов;
2) каждый член представляет собой произведение  элементов, взятых по одному из каждой строки и каждого столбца; сомножители располагаются так, чтобы первым был элемент из первой строки, вторым - элемент из второй строки и т.д.;
элементов, взятых по одному из каждой строки и каждого столбца; сомножители располагаются так, чтобы первым был элемент из первой строки, вторым - элемент из второй строки и т.д.;
3) член берется со знаком плюс, если число инверсий в перестановке вторых индексов сомножителей четное, и со знаком минус в противном случае.
Итак, согласно определению имеем:

Суммирование здесь - распространяется на все перестановки  , которые можно составить из чисел
, которые можно составить из чисел  .
.
Рассмотрим некоторые частные случаи.
Итак,  . Такой определитель в общем виде записывается следующим образом:
. Такой определитель в общем виде записывается следующим образом:
 .
.
Членом такого определения будет произведение вида:

где 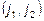 - любая перестановка из чисел 1, 2. Таких перестановок две:
- любая перестановка из чисел 1, 2. Таких перестановок две:  . Однако, в первом случае имеют
. Однако, в первом случае имеют  инверсий
инверсий  , во втором одну
, во втором одну  . Тогда для первого случая отмечают, что здесь четное число инверсий, во втором случае - нечетное. В связи с отмеченным имеют:
. Тогда для первого случая отмечают, что здесь четное число инверсий, во втором случае - нечетное. В связи с отмеченным имеют:
 .
.
Словесно такое соотношение формулируется так: определитель второго порядка, соответствующий квадратной матрице второго порядка, равен разности произведения элементов, стоящих на главной диагонали, и элементов, стоящих на побочной ее диагонали.
|
|
|
Рассмотрим случай, когда  . Здесь имеют определитель вида
. Здесь имеют определитель вида
 .
.
Членами определителя третьего порядка является произведение вида:  где
где  перестановки из чисел
перестановки из чисел  . Таких перестановок шесть:
. Таких перестановок шесть:

Следует отметить, что первая группа перестановок имеет четное число инверсий, вторая - нечетное, в связи с чем имеют:


|
|
|


