Источники и виды неопределенности.

Возникающие в управленческой деятельности неожиданные ситуации достаточно часто требуют срочных и часто неординарных действий, сопряженных с риском. Появившиеся проблемы и связанный с их решением риск может иметь явный и неявный характер. Все зависит от поступающей информации. В первом случае она более определенна, во втором - слабо сигнализирует о надвигающейся опасности. Очень важно не игнорировать сигналы, а усилить наблюдение за ходом событий.

Известно, по критерию определенности информации различают решения, принятые в условиях: а) определенности, б) вероятностной определенности (риска), в) в условиях неопределенности (ненадежности). Если решение принимается в условиях определенности (достоверности), то увеличивается оперативность разработки, уменьшаются затраты на выбор целесообразного варианта. Преимущество подобной ситуации: все переменные для расчетов вводятся самим субъектом управления при одном и том же состоянии объективных условий (объекта). В практической работе нередки случаи отсутствия полной определенности ситуации. Тогда вычленяются ее элементы из общего контекста по степени их определенности. Если решение принимается в условиях риска (измеримой неопределенности), то с помощью введения вероятностных оценок неопределенность в значительной мере уменьшается. Колебания переменных, характеризующих состояние объективных условий, могут быть предугаданы. Риск заключается в возможных ошибках при оценке степени вероятности наступления условий (событий). Поэтому полагаются не только на расчеты, используются также опыт, интуиция и искусство руководителя. Эти качества особенно необходимы при разработке решений в условиях неопределенности, когда установить вероятность наступления событий и потенциальных результатов невозможно. Происходит это под воздействием новых, сложных факторов, учесть которые затруднительно.

№30. Многокритериальные модели выбора решений. Схемы компромисса в многокритериальных моделях выбора решений: принцип выделение главного критерия, принципы равенства и квазиравенства, принципы гарантированного уровня и интегральной эффективности.

Многокритериальные задачи принятия решений.

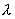Пусть, необходимо выбрать одно из множества решений X из области xих допустимых значений. Каждое выбранное решение оценивается совокупностью критериев f1,f2,…,fk, которые могут различаться своими коэффициентами относительной важности ( 1… 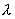k). Критерии fq, q=1..k, называют частными или локальными критериями, они образуют интегральный или векторный критерий оптимальности F={fq}. Коэффициенты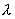 образуют вектор важности . Каждый локальный критерий характеризует некоторую локальную цель принимаемого решения.

Оптимальное решение X должно удовлетворять соотношению:

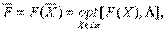где: F – оптимальное решение интегрального критерия; opt – оператор оптимизации, он определяет выбранный принцип оптимизации.

Область допустимых решений xможет быть разбита на две непересекающиеся части: 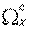– область согласия, в которой качество решения может быть улучшено одновременно по всем локальным критериям или без снижения уровня любого из критериев; – область компромиссов, в которой улучшение качества решения по одним локальным критериям приводит к ухудшению качества решения по другим.

Очевидно, что оптимальное решение может принадлежать только области компромиссов, так как в области согласия решение может и должно быть улучшено по соответствующим критериям.

Выделение области компромисса сужает область возможных решений, но для выбора одного-единственного варианта решения необходимо выбрать схему компромисса, то есть раскрыть смысл оператора оптимизации opt. Этот выбор осуществляется субъективно.

Рассмотрим основные схемы компромисса, предполагая вначале, что все локальные критерии нормализованы (то есть имеют одинаковую размерность или являются безразмерными величинами) и одинаково важны. Рассмотрение удобно вести, перейдя от пространства x выбираемых решений X к пространству k возможных (допустимых) локальных критериев F={f1,f2,…,fk}, деля его на область согласия и область компромиссов.

Тогда сформулированную ранее модель оптимизации можно переписать в виде:

Основными схемами компромисса являются:

- принцип равномерности;

- принцип справедливой уступки;

- принцип выделения одного оптимизируемого критерия;

- принцип последовательной уступки.

Принцип равномерности провозглашает целесообразность выбора такого варианта решения, при котором достигалась бы некоторая “равномерность” показателей по всем локальным критериям. Используют следующие реализации принципа равномерности:

- принцип равенства;

- принцип максимина;

- принцип квазиравенства.

Принцип равенства формально выражается следующим образом:

,

то есть оптимальным считается вариант, принадлежащий области компромиссов, при котором все значения локальных критериев равны между собой. Однако случай f1=f2=…=fkможет не попасть в область компромиссов или вообще не принадлежать к области допустимых вариантов. Принцип квазиравенства заключается в том, что стремятся достичь приближённого равенства всех локальных критериев. Приближение характеризуется некоторой величиной . Это принцип может быть использован в дискретном случае.

Следует отметить, что принципы равенства, несмотря на их привлекательность, не могут быть рекомендованы во всех случаях. Иногда даже небольшое отклонение от равномерности может дать значительный прирост одному из критериев. Принцип выделения одного оптимизируемого критерия формально может быть записан следующим образом: ,где fi-оптимизируемый критерий при условиях: 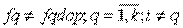; fqdop. - допустимое значение критерия. Один из критериев является оптимизируемым и выбирают тот вариант, при котором достигается максимум этого критерия. На другие критерии накладываются ограничения.