 |
Регрессионный анализ.
|
|
|
|
Величина коэффициента корреляции позволяет вытеснить тесноту (силу) и направление связи, однако этим не исчерпываются возможности изучения сопряжённости между признаками. Более того, во многих исследованиях возникает необходимость изучить не столько меру корреляции, сколько форму её и характер изменения одного признака в зависимости от изменения другого. Последнее особенно важно в тех случаях, когда фактические наблюдения не охватывают всего разнообразия признака и цель исследования заключается в том, чтобы выяснить взаимозависимости между недостающими данными. Например, при изучении влияния дозы азотного удобрения, вносимого под ячмень, на содержание белка в зерне, научный интерес представляет не только установление тесноты связи и её направленность между этими изучаемыми показателями, но и на сколько повышается белковость зерна от каждого килограмма внесённого в почву азота.
Регрессионный анализ заключается в том, чтобы отыскать линию (прямую в случае линейной корреляции, параболу первого, второго и т.д. порядка при криволинейной зависимости) наиболее точно выражающую зависимость одного признака от другого. Кроме того, при помощи регрессионного анализа можно выяснить ошибку опытных данных, влияющих на конечные результаты исследования.
Существует множество аналитических методов определения регрессии, которые зависят от типа регрессии (парная или множественная), а также от типа, по которому отмечается взаимосвязь (прямая линия, гипербола, парабола и т.д.).
Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:
|
|
|
прямой 
;
гиперболы 
параболы 
и т.д.
Определить тип уравнения можно, исследуя зависимость графически, однако в практике не часто прибегают к этому методу определения уравнения.
Оценка параметров уравнений регрессии (а, b1, b2…) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
SS = 
→ min
Рисунок 8. Прямая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
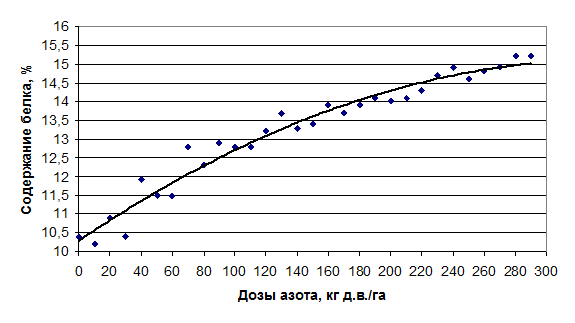
Рисунок 9. Параболическая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
В отношении установленной зависимости между дозами азотного удобрения и содержания белка в зерне ячменя данное правило можно интерпретировать так: прямая линия должна быть максимально приближена ко всем значениям ху или ух, что отчётливо отмечается на графике (рисунок 2 и рисунок 3)
Задача регрессионного анализа состоит в том, чтобы установить параметры уравнения регрессии (а, b1, b2…) или иными словами, описать взаимосвязь между изучаемыми показателями с помощью уравнения, оценить на какую величину изменяется значение результативного признака, при изменении факторного на единицу.
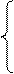Нахождение параметров линейной парной регрессии общепринятым методом осуществляется решением системы нормальных уравнений следующего вида:
, (65)
где n – объём исследуемой совокупности (число единиц наблюдений).
В уравнениях регрессии параметр a показывает усреднённое влияние на результативный признак неучтённых в уравнении факторных признаков: коэффициент регрессии b показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения. Таким образом, решая данную систему нормальных уравнений задача состоит именно в определении параметров уравнения регрессии a и b.
|
|
|
Уравнение линейной регрессии , в сельскохозяйственных и биологических исследованиях нередко представляют несколько в другом виде:
, (66)
или аналогично для нахождения теоретической линии регрессии х по у: 
, (67)
где 
и 
- средние арифметические для ряда х и у;
- коэффициент регрессии у по х,
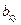- коэффициент регрессии х по у.
Коэффициенты регрессии вычисляются по формулам:
; (68)
. (69)
Числители этих формул представляют собой сумму произведений отклонений значений х и у от своих средних (то есть числитель формулы (64) расчёта коэффициента корреляции), а знаменатели – сумму квадратов отклонений от средних. Таким образом, связь между коэффициентов корреляции и коэффициентом регрессии можно математически выразить так:
; 
. (70, 71)
Произведение коэффициентов регрессии равно коэффициенту детерминации:
= RI (72)
При регрессионном анализе проводят обычно две оценки выборочных коэффициентов регрессии: а) оценки величины отклонений от линии регрессии и б) оценку существенности b, то есть значимость отклонения его от нуля.
Ошибка коэффициента регрессии вычисляется по формуле:
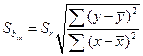и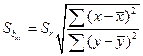 
. (73, 74)
Критерий существенности коэффициента регрессии определяют по формуле:
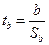(75)
Существенность коэффициента регрессии оценивают по приложению II, число степеней свободы df принимают равным n–2.
ПРИЛОЖЕНИЯ
Приложение I
Значения критерия ω (по Н.Ф. Деревицкому)
| Число степеней свободы | Уровень значимости | Число степеней свободы 5%-ный | Уровень значимости | ||
| 5%-ный | 1%-ный | 5%-ный | 1%-ный | ||
| 1,41 | 1,41 | 1,93 | 2,45 | ||
| 1,64 | 1,72 | 1,93 | 2,45 | ||
| 1,76 | 1,92 | 1,93 | 2,46 | ||
| 1,81 | 2,05 | 1,93 | 2,46 | ||
| 1,85 | 2,14 | 1,94 | 2,47 | ||
| 1,87 | 2,21 | 1,94 | 4,47 | ||
| 1,88 | 2,26 | 1,94 | 2,48 | ||
| 1,90 | 2,29 | 1,94 | 2,48 | ||
| 1,90 | 2,32 | 1,94 | 2,49 | ||
| 1,91 | 2,34 | 1,94 | 2,49 | ||
| 1,92 | 2,35 | 1,94 | 2,50 | ||
| 1,92 | 2,38 | 1,94 | 2,50 | ||
| 1,92 | 2,39 | 1,94 | 2,50 | ||
| 1,92 | 2,41 | 1,94 | 2,51 | ||
| 1,93 | 2,42 | 1,95 | 2,53 | ||
| 1,93 | 2,43 | 1,95 | 2,54 | ||
| 1,93 | 2,44 | 1,96 | 2,55 | ||
| 1,96 | 2,58 |
|
|
|
Приложение II
Стандартные значения критерия t (критерия Стьюдента) на 5%-ном, 1%-ном и 0,1%-ном уровне значимости (округлены до десятых)
| Число степеней свободы | Уровень значимости | Число степеней свободы | Уровень значимости | ||||
| 0,05 | 0,01 | 0,001 | 0,05 | 0,01 | 0,001 | ||
| 12,7 | 63,7 | 637,0 | 2,2 | 3,0 | 4,1 | ||
| 4,3 | 9,9 | 31,6 | 14-15 | 2,1 | 3,0 | 4,1 | |
| 3,2 | 5,8 | 12,9 | 16-17 | 2,1 | 2,9 | 4,0 | |
| 2,8 | 4,6 | 8,6 | 18-20 | 2,1 | 2,9 | 3,9 | |
| 2,6 | 4,0 | 6,9 | 21-24 | 2,1 | 2,8 | 3,8 | |
| 2,4 | 3,7 | 6,0 | 25-28 | 2,1 | 2,8 | 3,7 | |
| 2,4 | 3,5 | 5,3 | 29-30 | 2,0 | 2,8 | 3,7 | |
| 2,3 | 3,4 | 5,0 | 31-34 | 2,0 | 2,7 | 3,7 | |
| 2,3 | 3,3 | 4,8 | 35-42 | 2,0 | 2,7 | 3,6 | |
| 2,2 | 3,2 | 4,6 | 43-62 | 2,0 | 2,7 | 3,5 | |
| 2,2 | 3,1 | 4,4 | 63-175 | 2,0 | 2,6 | 3,4 | |
| 2,2 | 3,1 | 4,3 | ≥176 | 2,0 | 2,6 | 3,3 |
Приложение III
Наиболее значимые стандартные значения критерия F (критерия Р.Фишера) на 5%-ном, 1%-ном (жирным шрифтом) уровне значимости
(округлены до десятых)
| Число степеней свободы для меньшей дисперсии (df2) | Число степеней свободы для большей дисперсии (df1) | ||||||||||
| |||||||||||
| 6,0 13,7 | 5,1 10,9 | 4,8 9,8 | 4,5 9,2 | 4,4 8,8 | 4,3 8,5 | 4,2 8,3 | 4,2 8,1 | 4,0 7,7 | 3,8 7,3 | 3,7 6,9 | |
| 5,6 12,3 | 4,7 9,6 | 4,4 8,5 | 4,1 7,9 | 4,0 7,5 | 3,9 7,2 | 3,8 7,0 | 3,7 6,8 | 3,6 6,5 | 3,4 6,1 | 3,2 5,7 | |
| 5,3 11,3 | 4,5 8,7 | 4,1 7,6 | 3,8 7,0 | 3,7 6,3 | 3,6 6,4 | 3,5 6,2 | 3,4 6,0 | 3,3 5,7 | 3,1 5,3 | 2,9 4,9 | |
| 5,1 10,6 | 4,3 8,0 | 3,9 7,0 | 3,6 6,4 | 3,5 6,1 | 3,4 5,8 | 3,3 5,6 | 3,2 5,5 | 3,1 5,1 | 2,9 4,7 | 2,7 4,3 | |
| 5,0 10,0 | 4,1 7,6 | 3,7 6,6 | 3,5 6,0 | 3,3 5,6 | 3,2 5,4 | 3,1 5,2 | 3,1 5,1 | 2,9 4,7 | 2,7 4,3 | 2,5 3,9 | |
| 4,8 9,7 | 4,0 7,2 | 3,6 6,2 | 3,4 5,7 | 3,2 5,3 | 3,1 5,1 | 3,0 4,9 | 3,0 4,7 | 2,8 4,4 | 2,6 4,0 | 2,4 3,6 | |
| 4,8 9,3 | 3,9 6,9 | 3,5 6,0 | 3,3 5,4 | 3,1 5,1 | 3,0 4,8 | 2,9 4,6 | 2,8 4,5 | 2,7 4,2 | 2,5 3,8 | 2,3 3,4 | |
| 4,7 9,1 | 3,8 6,7 | 3,4 5,7 | 3,2 5,2 | 3,0 4,9 | 2,9 4,6 | 2,8 4,4 | 2,8 4,3 | 2,6 4,0 | 2,4 3,6 | 2,2 3,2 | |
| 4,6 8,9 | 3,7 6,5 | 3,3 5,6 | 3,1 5,0 | 3,0 4,7 | 2,9 4,5 | 2,8 4,3 | 2,7 4,1 | 2,5 3,8 | 2,3 3,4 | 2,1 3,0 | |
| 4,5 8,7 | 3,7 6,4 | 3,3 5,4 | 3,1 4,9 | 2,9 4,6 | 2,8 4,3 | 2,7 4,1 | 2,6 4,0 | 2,5 3,7 | 2,3 3,3 | 2,3 2,9 | |
| 4,5 8,5 | 3,6 6,2 | 3,2 5,3 | 3,0 4,8 | 2,9 4,4 | 2,7 4,2 | 2,7 4,0 | 2,6 3,9 | 2,4 3,6 | 2,2 3,2 | 2,0 2,8 | |
| 4,4 8,3 | 3,6 6,0 | 3,2 5,1 | 2,9 4,6 | 2,8 4,3 | 2,7 4,0 | 2,6 3,8 | 2,5 3,7 | 2,3 3,4 | 2,1 3,0 | 1,9 2,6 | |
| 4,4 8,1 | 3,5 5,9 | 3,1 4,9 | 2,9 4,4 | 2,7 4,1 | 2,6 3,9 | 2,5 3,7 | 2,4 3,6 | 2,3 3,2 | 2,1 2,9 | 1,8 2,4 | |
| 4,3 7,9 | 3,4 5,7 | 3,1 4,8 | 2,8 4,3 | 2,7 4,0 | 2,6 3,8 | 2,5 3,6 | 2,4 3,5 | 2,2 3,1 | 2,0 2,8 | 1,8 2,3 | |
| 4,3 7,8 | 3,4 5,6 | 3,0 4,7 | 2,8 4,2 | 2,6 3,9 | 2,5 3,7 | 2,4 3,5 | 2,4 3,3 | 2,2 3,0 | 2,0 2,7 | 1,7 2,2 | |
| 4,2 7,7 | 3,4 5,5 | 3,0 4,6 | 2,7 4,1 | 2,6 3,8 | 2,5 3,6 | 2,4 3,4 | 2,3 3,3 | 2,2 3,0 | 1,9 2,6 | 1,7 2,1 | |
| 4,2 7,6 | 3,3 5,4 | 2,9 4,5 | 2,7 4,0 | 2,5 3,7 | 2,4 3,5 | 2,3 3,3 | 2,3 3,2 | 2,1 2,8 | 1,9 2,5 | 1,6 2,0 | |
|
| 3,8 6,6 | 3,0 4,6 | 2,6 3,8 | 2,4 3,3 | 2,2 3,0 | 2,1 2,8 | 2,0 2,6 | 1,9 2,5 | 1,8 2,2 | 1,5 1,8 | 1,0 1,0 |
|
|
|
|
|
|
