 |
Понятие о мертвых положениях в кривошипно-ползунных механизмах
|
|
|
|
В большинстве кривошипных механизмов имеются т. н. мертвые положения, в которых передача движения на кривошип невозможна и при выходе из которых ведомый кривошип может изменить направление вращения на обратное. Прохождение этих положений в поршневых двигателях обычно обеспечивается инерцией звеньев. При ведущем кривошипе вблизи мертвых положений кривошипный механизм дает значительный выигрыш в силе, что используется в прессах и других рабочих машинах для получения больших сил на ползуне. Сложное движение шатунов кривошипных механизмов иногда используют для привода рабочих органов некоторых машин — тестомесилок, снегопогрузчиков и других.
Волновые передачи
Волнова́я передача — механическая передача, передающая движение за счет циклического возбуждения волн деформации в гибком элементе. Передача движения может производиться посредством зубьев, винтового принципа, а также фрикционного контакта. Изобретена в 1959 году американским инженером У. Массером.
Принцип действия
Детали волновых зубчатых передач
Состоит из жесткого неподвижного элемента — зубчатого колеса с внутренними зубьями, неподвижного относительно корпуса передачи; гибкого элемента — тонкостенного упругого зубчатого колеса с наружными зубьями, соединенного с выходным валом; генератора волн — кулачка, эксцентрика или другого механизма, растягивающего гибкий элемент до образования в двух (или более) точках пар зацепления с неподвижным элементом. Число зубьев гибкого колеса несколько меньше числа зубьев неподвижного элемента. Число волн деформации равно числу выступов на генераторе. В вершинах волн зубья гибкого колеса полностью входят в зацепление с зубьями жёсткого, а во впадинах волн — полностью выходят из зацепления. Линейная скорость волн деформации соответствует скорости вершин выступов на генераторе, то есть в гибком элементе существуют бегущие волны с известной линейной скоростью. Разница чисел зубьев жёсткого и гибкого колёс обычно равна (реже кратна) числу волн деформации.
|
|
|
Принцип работы волновой зубчатой передачи
Например, при числе зубьев гибкого колеса 200, неподвижного элемента — 202 и двухволновой передаче (два выступа на генераторе волн) при вращении генератора по часовой стрелке первый зуб гибкого колеса будет входить в первую впадину жёсткого, второй — во вторую и т.д. до двухсотого зуба и двухсотой впадины. На следующем обороте первый зуб гибкого колеса войдёт в двести первую впадину, второй — в двести вторую, а третий — в первую впадину жёсткого колеса. Таким образом, за один полный оборот генератора волн гибкое колесо сместится относительно жёсткого на 2 зуба.
Конструкция волнового редуктора
Достоинства и недостатки
Достоинства
большое передаточное отношение, при малом количестве деталей (i = 80-320)
улучшенные массо-габаритные характеристики по сравнению с обычными зубчатыми передачами
высокая кинематическая точность и плавность хода
высокая нагрузочная способность
передача момента через герметичные стенки
Недостатки:
высокая напряженность основных элементов гибкого колеса и генератора волн пониженная крутильная жесткость.
Билет №7
1.Кривошипно-кулисный механизм
Кривошипно-кулисный механизм с качающейся кулисой (рис. 38, II) служит для преобразования вращательного движения кривошипа 3 в качательное движение кулисы 1 и при этом происходит быстрый ход при движении ползуна в одну сторону и медленный — в другую. Механизм широко применяется в металлорежущих станках, например: в поперечно-строгальных, зубодолбежных и др.
|
|
|
Кривошипно-кулисный механизм с поступательно движущейся кулисой (рис. 38, III) служит для преобразования вращательного движения кривошипа 3 в прямолинейно-поступательное движение кулисы 1. В механизме кулиса может быть расположена вертикально или наклонно. Применяется такой механизм для малых длин хода и находит широкое применение в счетных машинах (синусный механизм).
Кривошипно-кулисные механизмы могут иметь вращающуюся, качающуюся или поступательно-движущуюсякулису (см. Кривошипный механизм). Кулисно-коромысловые механизмы, получающиеся из предыдущих приограничении угла поворота кривошипа, выполняют с качающейся (рис. 1, а) и поступательно-движущейся(рис. 1, б) кулисой, применяют для преобразования движения, а также в качестве т. н. синусных механизмов(рис. 1, в) счётно-решающих машин. Кулисно-ползунные механизмы предназначаются для преобразованиякачательного движения в поступательное или наоборот, а также используются в качестве тангенсногомеханизма в счётно-решающих машинах. В машинах находят применение двухкулисные механизмы (рис. 2),обеспечивающие равенство угловых скоростей кулис при постоянном угле между ними. Это свойствоиспользуют, например, в Муфтах, допускающих смещение осей соединяемых валов. Сложные многозвенныеК. м. применяют для различных целей, например в системах регулирования наполнения цилиндровдвигателей внутреннего сгорания, реверсивных механизмах паровых машин и др.
Н. Я. Ниберг.
Рис. 1. Кулисно-коромысловый механизм: а — с качающейся кулисой; б — с поступательно—движущейся кулисой; в — синусный: r sin φ — плечо перемещения кулисы при повороте её на угол φ.
Рис. 2. Двухкулисный механизм.
2. Статистическое уравновешивание рычажных механизмов
Если главный вектор сил инерции, который представляет собой векторную сумму сил инерции всех подвижных звеньев (например, рис.5.4),,то такой механизм называется статически уравновешенным.
Если главный момент сил инерции, который представляет собой векторную сумму инерционных моментов всех подвижных звеньев (например, рис.5.4),,,то такой механизм называется моментно уравновешенным.
Статическое уравновешивание механизма можно добиться только тогда, когда ускорение aS общего центра масс, обозначенного точкой S равно нулю, так как в этом случае результирующая сила инерции подвижных звеньев
|
|
|
Билет №8
1.Кинетостатический расчет механизмов
Силовой анализ механизма имеет целью выявление действующих в нем сил. Так как при силовом анализе рассматривается механизм, находящийся в движении, то этот анализ называется кинетостатическим. В основу кинетостатического анализа положен принцип Даламбера, предполагающий учет сил инерции звеньев механизма.
Основные положения, которых следует придерживаться при силовом анализе:
1. Звенья механизма считают абсолютно твердыми (недеформируемыми), а элементы кинематических пар - абсолютно гладкими (без трения).
2. Выполняется условие статической определимости механизма.
3. Силовой анализ механизма проводится по статически определимым группам Ассура. Начинается анализ с исследования группы Ассура, наиболее удаленной от ведущей части схемы - механизма 1 класса. Заканчивается силовой анализ исследованием механизма 1 класса.
4. Силы инерции условно переносятся по линиям их действия на ускоряемые массы.
5. Расчетные уравнения записываются в форме уравнений равновесия.
Способ определения неизвестных усилий - графический, путем построения планов сил.
2.Золотое правило механники
ще в древности при применении простых машин (рычаг, блок, ворот и т. д.) была обнаружена замечательная особенность всех этих машин: оказалось, что в простых машинах перемещения вполне определенным образом связаны с силами, развиваемыми машиной. Именно, отношение перемещений двух концов простой машины, к которым приложены силы, всегда обратно отношению сил, приложенных к этим концам.
Рис. 156. Сила, действующая на левое плечо рычага, в n раз больше силы, действующей на правое плечо. Перемещение s1, левого плеча в n раз меньше перемещения s2 правого плеча.
Например, если для равновесия рычага сила F1 должна быть в n раз больше, чем сила F2 (рис. 156), то при вращении рычага перемещение s1 его первого конца будет в n раз меньше, чем перемещение s2 второго конца. Для двойного блока такое же соотношение получается между силами, приложенными к веревкам, намотанным на оба блока и удерживающим его в равновесии, и перемещениями концов веревок при вращении блока. Это обстоятельство было сформулировано еще в древности следующим образом: «то, что мы выигрываем в силе, мы проигрываем в пути». Положение это имеет столь общее и вместе с тем столь важное значение, что оно получило название «золотого правила» механики.
|
|
|
Пользуясь введенными обозначениями, можем выразить «золотое правило» следующей формулой:
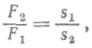или F1s1=F2s2.
В дальнейшем типы движений и характер машин, с которыми приходилось иметь дело в механике, все более и более усложнялись, и оказалось, что в таком простом виде «золотое правило» механики не всегда справедливо. Но попутно с усложнением видов движений и типов машин постепенно дополнялось и усложнялось «золотое правило» механики так, чтобы оно охватывало и более сложные случаи. При этом из «золотого правила» возникли важнейшие физические представления о работе и энергии. Вместе с тем «золотое правило» механики явилось первой простейшей формулировкой одного из основных законов природы — закона сохранения энергии, который оказался справедливым для всех без исключения явлений в природе.
Для выяснения понятий работы и энергии мы рассмотрим «золотое правило» механики более подробно. Чтобы упростить рассмотрение, мы сначала будем предполагать, что силы трения отсутствуют. Затем мы выясним, как изменится вся картина при учете сил трения.
«Золотое правило» механики практически соблюдается только в тех случаях, когда движение простых машин происходит равномерно, или с малыми ускорениями1). Например, при вращении двойного блока концы веревок, навитых на скрепленные между собой блоки радиусов r1 и r2, переместятся на расстояния s1 и s2, пропорциональные этим радиусам:
Значит, для того чтобы «золотое правило» было справедливо для двойного блока, должно быть выполнено условие
Тогда силы F1 и F2 уравновесятся и, значит, машина должна либо покоиться, либо двигаться равномерно. Но для того, чтобы привести в движение двойной блок, нужно нарушить равновесие, прибавив к одной из сил, например к F1, некоторую силу f (рис. 157). Возникающее движение будет ускоренным (напомним, что, по нашему предположению, трение отсутствует). При этом (F1+f) s1>F2s2—при движении двойного блока с ускорением «золотое правило» не соблюдается. Но чем меньше сила f по сравнению с F1, тем ближе друг к другу произведения силы на путь для обоих концов блока и тем меньше отклонение от «золотого правила». При очень малых f движение будет происходить с очень малым ускорением, т. е. будет близко к равномерному.
|
|
|
Итак, «золотое правило» механики соблюдается вполне точно при равномерном движении (без трения) и приближенно при движении с малым ускорением. Ни одна машина не движется всегда равномерно: вначале она должна прийти в движение, а в конце должна остановиться. Но если пуск в ход и остановка двойного блока происходят с малым ускорением, то «золотое правило» механики практически справедливо во все время действия этой машины.
Рис. 157. Увеличив силу F1 на малую величину f, заставим блок вращаться с ускорением.
Таким же образом, как и для двойного блока, мы могли бы убедиться, что «золотое правило» механики справедливо и для всех простых машин при условии, что направления приложенных к машине сил и направления перемещений точек приложения сил совпадают. Для всех таких машин «золотое правило» механики справедливо в том виде, как мы вывели его для двойного блока: при равномерном движении машины (а практически также при движении с очень малыми ускорениями) произведения силы на перемещение точки приложения для обеих сил равны.
Билет №9
Червячные передачи
Червячные передачи – это передачи зацеплением с непосредственным контактом витков червяка и зубьев червячного колеса (рис. 12.1). Червяк 1 – это винт с трапецеидальной или близкой к ней по форме резьбой. Червячное колесо является косозубым зубчатым колесо с зубьями особой дуговой формы. Такая форма зубьев обеспечивает увеличение их длины и прочности зубьев на изгиб.
|
| Рис. 12.1 |
Червячные передачи применяют при необходимости передачи движения между перекрещивающимися (как правило взаимно перпендикулярными) валами. При вращении червяка его витки плавно входят в зацепление с зубьями колеса и приводят его во вращение. Передачи используют в станках, автомобилях, подъемно-транспортных и других машинах.
12.2. Достоинства и недостатки червячных передач
Достоинства:
возможность получения большого передаточного числа в одной ступени;
плавность и малошумность работы;
повышенная кинематическая точность.
Недостатки:
низкий КПД;
необходимость изготовления зубьев колеса из дорогих антифрикционных материалов;
повышенные требования к точности сборки, необходимость регулировки;
необходимость специальных мер по интенсификации теплоотвода.
12.3. Типы червяков
По форме тела червяки разделяют на цилиндрические, глобоидные и тороидные. Наибольшее применение находят цилиндрические червяки как более простые в изготовлении и обеспечивающие достаточно высокую нагрузочную способность.
Профиль витков червяка можно варьировать, так как червячные колеса изготовляют инструментом, являющимся аналогом червяка. По форме боковой поверхности витка червяки разделяют на архимедовы (обозначение ZA), конволютные (ZN), эвольвентные (Z1), нелинейчатые с поверхностью, образованной конусом (ZK) и с вогнутым профилем витка (ZT).
При невысоких требованиях к нагрузочной способности и ресурсу в условиях мелкосерийного производства применяют архимедовы и конволютные червяки. Витки архимедовых червяков имеют прямолинейный профиль в осевом сечении, в торцовом сечении витки очерчены архимедовой спиралью (рис. 12.2, а,г). Витки конволютных червяков имеют прямолинейный профиль в сечении, нормальном к направлению витка, в торцовом сечении витки очерчены удлиненной эвольвентой (рис.12.2, б,д). Нарезание архимедовых и конволютных червяков выполняют на универсальных токарно-винторезных станках. Для шлифования архимедовых червяков требуется круг, очерченный сложной кривой в осевом сечении, что ограничивает их применение. Шлифование конволютных червяков конусными кругами с прямолинейными образующими на обычных резьбошлифовальных станках приводит к небольшому искривлению прямолинейного профиля витка, поэтому такие червяки называют “нелинейчатыми”. Червячные фрезы для нарезания червячных колес шлифуют тем же способом, поэтому получают правильное зацепление.
Определение числа степеней подвижности плоских механизмов
Пусть мы имеем n звеньев, из которых собирается кинематическая цепь. Пока звенья не соединены в кинематические пары, каждое из них имеет шесть степеней свободы (степеней подвижности). Все звенья до соединения в кинематическую цепь следовательно имели 6n степеней подвижности. После сборки звеньев в кинематическую цепь мы получим кинематические пары различных классов (с разными степенями подвижности). Предположим, что наша кинематическая цепь имеет кинематические пары всех пяти классов. Примем следующие обозначения:
Р5- количество кинематических пар пятого класса в образованной нами кинематической цепи,
Р4 - количество кинематических пар четвёртого класса,
Р3- количество кинематических пар третьего класса,
Р2- количество кинематических пар второго класса,
Р1- количество кинематических пар первого класса.
Каждая кинематическая пара ограничивает перемещение звеньев, отбирает у них столько степеней свободы, как её класс. Каждая кинематическая пара 5 класса отбирает у звеньев 5 степеней свободы. Все пары пятого класса отнимут у звеньев 5Р5 степеней свободы, четвёртого класса - 4Р4, третьего - 3Р3, второго - 2Р2, первого - 1Р1. Если из общего количества степеней свободы звеньев 6n вычесть все потерянные степени свободы, получим число степеней подвижности кинематической цепи W: W=6n-5P5-4Р4-3Р3-2Р2-1P1. (1)
Степенью подвижности механизманазывается количество независимых координат, которые необходимо задать для определения положений звеньев механизма в системе координат, жестко связанной со стойкой.
Механизм отличается от кинематической цепи тем, что у него одно звено полностью закреплено. Закрепленное звено потеряло все шесть степеней свободы. Следовательно в механизме число подвижных звеньев равно n-1. Подставив в формулу (1) количество подвижных звеньев n-1, получим формулу для определения степени подвижности механизма:
W=6(n-1)-5P5-4Р4-3Р3-2Р2-1P1. (2)
Формула (2) впервые была получена Малышевым для пространственных механизмов.
Рассмотрим формулу Малышева для определения степени подвижности плоских механизмов. Все звенья плоского механизма могут иметь три степени подвижности, а кинематические пары соответственно могут иметь 1 или 2 степени подвижности. Если плоские кинематические пары рассматривать по классам, то они могут быть только пятого и четвёртого классов. При этом необходимо учесть, что общее количество степеней подвижности всех звеньев плоского механизма равно 3(n-1). Пары пятого класса теряют две степени подвижности, четвёртого –одну. Таким образом степень подвижности плоского механизма может быть определена по формуле:
W=3(n-1)-2P5-Р4. (3)
Формула (3) для определения степени подвижности плоского механизма впервые была получена Чебышевым П. Л.
В зависимости от числа общих условий связей, накладываемых на механизм, механизмы подразделяют на семейства.
Семейства механизмов и их структурные формулы приведены в таблице 1.
Таблица 2.1 Структурные формулы различных семейств механизмов
| Семейство | Структурная формула | Примечание |
| I II III IV | W=6(n-1)-5P5-4Р4-3Р3-2Р2-1P1 W=5(n-1)-4P5-3Р4-2Р3-Р2 W=4(n-1)-3P5-2Р4-Р3 W=3(n-1)-2P5-Р4 W=2(n-1)- P5 | Сомова- Малышева Чебышева Добровольского |
Рассмотрим применение структурной формулы Чебышева П. Л. на конкретном примере. На рисунке 5 изображен шарнирный четырёхзвенник.
1 е - звено- кривошип- совершает вращательное движение вокруг оси О (полный оборот);
2 е - звено АВ- шатун- совершает плоско- параллельное движение;
3 е - звено ВС- коромысло (или балансир)- совершает возвратно- вращательное движение вокруг оси С (неполный оборот);
4 е - звено ОС- стойка (станина)- неподвижное звено.
Количество звеньев n=4. Кинематические пары: 4-1, 1-2, 2-3, 3-4. Имеем 4 одноподвижные пары 5 го класса. Относительное движение всех звеньев плоское. Механизм плоский. Определяем степень подвижности его по формуле Чебышева П. Л.:
W=3(n-1)-2P5-Р4=3(4-1)-2×4-0=1.
Механизм имеет степень подвижности равную 1. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, жестко связанной со станиной, чтобы определить положения всех остальных звеньев. Например, в нашем случае достаточно задаться углом поворота кривошипа j1.
Пассивные связи и избыточные звенья
Звенья и кинематические пары, которые не влияют на характер движения механизма в целом, называются избыточными (лишними) звеньями и парами, а обусловленные ими связи называются пассивными связями.
При определении степени подвижности механизма избыточные звенья и кинематические пары не должны учитываться.
В сложных стержневых механизмах не всегда на глаз можно определить степень подвижности. В этих случаях необходимо воспользоваться формулой Чебышева.
Билет №10
Фрикционные передачи
Фрикционная передача (лат. frictio, родительный падеж frictionis — трение) — кинематическая пара, использующая силу трения между собой для передачи механической энергии.
Трение между элементами может быть сухое, граничное, жидкостное. Жидкостное трение наиболее предпочтительно, так как значительно увеличивает долговечность фрикционной передачи.
Классификация передач
Фрикционные передачи бывают:
с параллельными валами
с пересекающимися валами
с внешним контактом
с внутренним контактом
по возможности варьирования передаточного отношения
нерегулируемые (i=const)
регулируемые (фрикционный вариатор)
по возможности изменения передаточного отношения при наличии промежуточных тел в передаче по форме контактирующих тел
цилиндрические
конические
сферические
плоские
Применени
Валы прокатных станов, мотор-редуктор с фрикционным вариатором, ведущие колёса транспортных средств, взаимодействующих с опорной поверхностью посредством сил трения.
|
|
|
