Синтез кулачкового механизма

Кулачковым механизмом называется механизм, в состав которого входит кулачок (звено, рабочая поверхность которого имеет переменную кривизну). Зубчатый механизм можно рассматривать как многокулачковый механизм.

Кулачковые механизмы широко применяются в двигателях внутреннего сгорания, в текстильных машинах, в полиграфических машинах, в машинах – автоматах различного назначения, в разнообразных приборах. Достоинство кулачковых механизмов – возможность воспроизводить почти любой закон движения, причем синтез их относительно несложен. Недостатки – наличие высшей кинематической пары и, как следствие, ограниченная долговечность, сложность изготовления, высокая стоимость.

Кулачковый механизм состоит из кулачка (обычно вращающегося) и толкателя, совершающего возвратно – поступательное движение. Иногда толкатель совершает колебательное движение, в таком случае он называется колебателем или коромыслом. Для уменьшения трения толкатель снабжают роликом. Схемы кулачковых механизмов чрезвычайно разнообразны. Кулачковые механизмы бывают плоские и пространственные, с толкателем, имеющим рабочим элементом острие, ролик или плоскость, центральные и дезаксиальные (рис. 6.1).

Соприкосновение звеньев в кулачковом механизме обеспечивается силовым или геометрическим замыканием (рис. 6.2). Силовое замыкание осуществляется с помощью пружины. Геометрическое замыкание осуществляется с помощью паза, в котором помещается ролик толкателя. Недостатком такой конструкции является трудоемкость точного выполнения паза и наличие удара при реверсировании движения толкателя из-за неизбежного зазора между роликом и пазом. От этого недостатка свободен двухдисковый кулачок. Еще одну разновидность представляет диаметральный кулачок с рамочным толкателем. Его особенность состоит в том, что произвольно можно выбрать только часть профиля кулачка, оставшаяся часть профиля определяется из условия замыкания кулачка рамкой.

Билет №12

Теория зацепления

Эвольвента обладает следующими свойствами, которые используются в теории зацепления: форма эвольвенты определяется радиусом основной окружности;

нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;

эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.

Планетарные и дифференциальные механизмы

В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты). Такие механизмы называются планетарными (если имеют одну степень свободы) или дифференциальными (если степень свободы равна двум).

Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий кпд, более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.

а) б)

Рисунок 37 На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо "2" имеет подвижную геометрическую ось – это и есть сателлит.

Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью. Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса "1" и "3" – иногда такие колеса называют солнечными). Звено, соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается "H").

При кинематическом исследовании дифференциальных и планетарных механизмов применяется метод обращения движения (по-другому его называют методом остановки водила). Смысл этого метода заключается в том, что если всем звеньям системы добавить (с любым знаком) одну и ту же скорость, то характер относительного движения этих звеньев не изменится.

Рассмотрим решение с помощью этого метода на примере механизмов, изображенных на рисунке 37. Пусть звенья этого механизма имеют соответственно угловые скорости: ω₁, ω₂, ω₃, ω_H.

Добавим всем этим звеньям угловую скорость (– _H). Тогда они будут иметь следующие скорости: (ω₁– ω_H), (ω₂ – ω_H), (ω₃ – ω_H), (ω_H – ω_H) = 0. Водило стало неподвижным, значит и ось сателлита 2 также стала неподвижной, т.е. механизм превратился в обычный многоступенчатый механизм с неподвижными осями всех зубчатых колес.

Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):

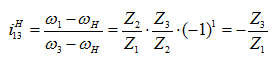Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления(с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.

В результате в уравнении его число зубьев сократилось, т.е. его число зубьев не влияет на общее передаточное отношения механизма. Такие колеса часто называют «паразитными», хотя правильно их называть ведомо-ведущими.

Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:

1) заданы ω₁ и ω₃; из записанной формулы определяется ω_H (вариант, изображенный на рисунке 37 а);

2) заданы ω₁ и ω_H; из записанной формулы определяется ω₃;

3) заданы ω_H и ω₃; из записанной формулы определяется ω₁.

Так как звеньям можно задавать любые законы движения, то, как частный случай, одному из центральных колес зададим угловую скорость, равную нулю. Например, в рассматриваемом механизме зададим ω₃=0, другим словами, затормозим третье колесо. Таким приемом отнимается одна из двух степеней свободы, и механизм из дифференциального превращается в планетарный (рисунок 37 б).

Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).

Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма:

Здесь приведен конкретный пример решения, но на самом деле на этом примере надо усвоить метод решения, подход к решению такого рода задач, т.к. метод один, но для каждой схемы механизма будут получаться свои уравнения.

4) Сложные механизмы

Существуют механизмы, включающие в свой состав различные части (обычные, планетарные, дифференциальные). В этом случае необходимо разделить механизм на части, записать уравнения передаточных отношений для каждой из них, используя соответствующий метод решения.

Совместным решением полученных алгебраических уравнений находят общее передаточное отношение механизма.

Билет №13

1.Геометрические параметры косозубых зубчатых колес имеют преимущественное распространение рис. 2.3.14.

;

Рис. 2.3.1 Цилиндрическая косозубая а) и шевронная б) передачаС увеличением угла наклона линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются рис.2.3.15, но при этом увеличивается и осевая сила Fа, что нежелательно. Поэтому в косозубых передачах принимают угол .

 

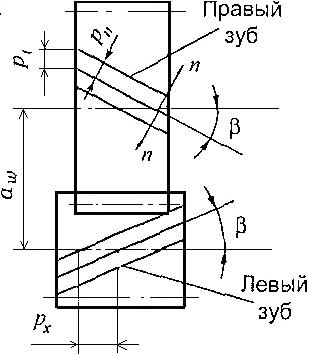
Рисунок 2.3.15 Геометрия косозубых колес

Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага: нормальный шаг зубьев pn - в нормальном сечении,
окружной шаг pt – в торцовом сечении; при этом
Соответственно шагам имеем два модуля зубьев:

(
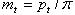(2.3.23)
(где mt и mn – окружной и нормальный модули зубьев. За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим: для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно заготовки на угол . Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m.
Диаметры делительный и начальный
(2

диаметр вершин и косых субьев

(2.3.26)

(2.3.27)

Межосевое расстояние

(2.3.28)

Эквивалентное веществоПрофиль косого колеса в нормальном сечении n-n (рис. 3) соответствует исходному контуру инструментальной р 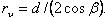ейки и, следовательно, совпадает с профилем прямозу: (2.3.29)
эквивалентное число зубьев: 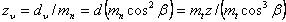(2.3.30)
или 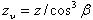(2.3.31)
где z – действительное число зубьев косозубого колеса. С увеличением возрастает возрастает . Это одна из причин повышения прочности косозубых передач.

Силы в зацеплении

Силы в зацеплении определяют в полюсе зацепления. Сила , действующая на зуб косозубого колеса рис. 2.3.16, направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет угол с касательной к эллипсу.

Рисунок 2.3.16Схема действия сил в зацеплении косозубых колес

 

Разложим эту силу на две составляющие: окружную силу на эквивалентном колесе: (2.3.22)
радиальную силу на этом колесе: 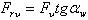(2.3.33)

Переходя от эквивалентного к косозубому колесу, заметим, что сила является радиальной силой и для этого колеса, т.е.

 

сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет угол с осью колеса. Разложим силу Ft на две составляющие:
окружную силу (2.3.35),
и осевую силу (2.3.36).

Окружная сила известна. Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса (2.3.37)

Тогда из формулы (2.3.35): следует Подставив силу и выражения , окончательно получим:

радиальную силу (2.3.38)
и осевую силу 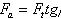(2.3.39).

На зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев (правое и левое). Наличие в зацеплении осевой силы, которая дополнительно нагружает валы и подшипники, является недостатком косозубых передач.

Расчет на контрактную площадьпределяют по формуле (2.3.17):

,где Ка = 43 МПа – для косозубых колес.
Контактные напряжения в поверхностном слое зубьев

,где 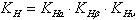- коэффициент нагрузки при расчете по контактным напряжениям;
- 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости;
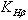- коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки;
- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки
=1,02-1,06 при любой твердости, скорость до 10 м/с,
=1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с,
=1,05 при твердости более 350 НВ и скорости 10-20 м/с.
Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент , меньше.
Условие контактной прочности косозубой передачи

,Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений . Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют.

Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес

Расчет зубьев на изгиб и . Формула проверочного расчёта косозубых передач

(2.3.41),где YF - коэффициент формы зуба выбирают по эквивалентному числу зубьев zv; - коэффициент, учитывающий наклон зуба; - коэффициент распределения нагрузки по ширине венца определяют по аналогии с прямозубыми передачами; = 0,81-0,91 - коэффициент распределения нагрузки между зубьями; 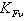- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки 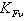=1,2 при твердости зубьев не больше 350НВ, 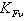= 1,1 при твердости зубьев более 350 НВ. Нормальный модуль зубьев mn определяют по аналогии с прямозубыми передачами. При некоторых средних значениях коэффициентов получим формулу для приближенного определения модуля косозубых передач

(2.3.42),

и для шеврочных передач

(2.3.43),

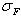При проверке по формуле (2.3.41): можно получить значительно меньше , что не является недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.Если расчётное значение 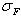превышает допускаемое, то применяют колёса, нарезанные с положительным смещением инструмента, или увеличивают m; 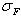> означает, что в передаче из данных материалов решающее значение имеет не контактная прочность, а прочность зубьев на изгиб. На практике к таким передачам относятся передачи с высокой твёрдостью рабочих поверхностей зубьев – 51…63HRCэ (цементация, нитроцементация, азотирование). Проектировочный расчёт таких передач следует выполнять с целью обеспечения прочности зубьев на изгиб по форме определения минимально допустимого модуля m, а затем выполнить проверочный расчёт зубьев на контактную прочность.

Гидравлические и пневматические механизмы

Гидравлические и пневматические исполнительные механизмы можно подразделять на поршневые, мембранные, лопастные как одностороннего, так и двустороннего действия. [ 1 ]

Гидравлические и пневматические исполнительные механизмы по принципу действия и конструктивному оформлению не имеют существенных различий. Однако отдельные узлы из-за различных свойств рабочих сред (жидкости и газа) имеют некоторые конструктивные особенности. В зависимости от рабочей среды выбирают материалы для деталей приводов (корпусов, поршней, штоков, диафрагм и др.), а также конструктивное оформление уплотнений движущихся деталей. [ 2 ]

Гидравлические и пневматические исполнительные механизмы характеризуются простотой конструкции, большими выходными моментами, надежностью и возможностью получать различные скорости перемещения регулирующего органа. В качестве привода электрических исполнительных механизмов используют электродвигатели переменного или постоянного тока. [ 3 ]

Гидравлические и пневматические исполнительные механизмы характеризуются простотой конструкции, большими выходными моментами, надежностью и возможностью получать различные скорости перемещения регулирующего органа. В качестве привода электрических исполнительных механизмов используют электродвигатели переменного или постоянного тока. К недостаткам этих исполнительных механизмов следует отнести сложность регулирования скорости при использовании трехфазных электродвигателей. [ 4 ]

В машинах-автоматах с гидравлическими и пневматическими исполнительными механизмами не существует жесткой кинематической связи между движением рабочих органов; время перемещения рабочих органов определяется из уравнений динамики и зависит от ряда факторов, в том числе и случайных. Вследствие этого в автоматах с управлением от коммутационных барабанов, командоаппаратов и с системой управления путевой контроль совмещение фаз движения исполнительных механизмов может быть проведено лишь в тех случаях, когда отклонения во времени срабатывания рабочих органов исполнительных механизмов, выполняющих операции, последовательно идущие одна за другой, не могут привести к нарушению работы машины. [ 5 ]

Обслуживание и ремонт регуляторов прямого действия, гидравлических и пневматических исполнительных механизмов на технологическом оборудовании проводит цех, в котором установлено это оборудование. Механическую часть обдувочных аппаратов и выдвижных форсунок с электромеханическим приводом обслуживает и ремонтирует котельный цех. [ 6 ]

В материалах этого раздела впервые и весьма обстоятельно проведено сравнение гидравлических и пневматических исполнительных механизмов по большому числу факторов, определяющих их статические и динамические характеристики. В результате сделан вывод, что гидравлические механизмы при одинаковых нагрузках и подводимом давлении обладают в 50 раз. [ 7 ]

Основой реле времени механического типа является часовой механизм; в реле гидравлического и пневматического типов, которые обычно используются в машинах-автоматах с гидравлическими и пневматическими исполнительными механизмами, длительность выдержки определяется временем истечения жидкости или воздуха через калиброванное отверстие. [ 8 ]

Исполнительные механизмы с переменной скоростью перемещения имеют скорость перемещения выходного вала (или штока) переменную, зависящую от величины управляющего воздействия и пропорциональную ей. С пропорциональной скоростью работают гидравлические и пневматические исполнительные механизмы. [ 9 ]

К первой группе относятся в основном все электромоторные исполнительные механизмы переменного тока. Ко второй группе относятся гидравлические и пневматические исполнительные механизмы. [ 10 ]

Исполнительные механизмы с переменной скоростью перемещения имеют скорость перемещения выходного вала (или штока) переменную, зависящую от величины управляющего воздействия и пропорциональную ей. С пропорциональной скоростью работают гидравлические и пневматические исполнительные механизмы. [ 11 ]

В механизмах эпизодического действия Я может быть 1, что зависит от конкретных условий их использования. Начальным звеном может быть как звено /, так и поршень 3, как это имеет место в гидравлических и пневматических исполнительных механизмах. В гидравлическом исполнительном механизме скорость поршня определяется секундным расходом поступающей в цилиндр жидкости, в пневматическом механизме скорость должна быть определена в результате решения уравнений динамики и газодинамики.

В механизмах эпизодического действия А, может быть 5s 1, что зависит от конкретных условий их использования. Начальным звеном может быть как звено /, так и поршень 3, как это имеет место вгидравлических и пневматических исполнительных механизмах. В гидравлическом исполнительном механизме скорость поршня определяется секундным расходом поступающей в цилиндр жидкости, в пневматическом механизме скорость должна быть определена в результате решения уравнений динамики и газодинамики. [ 1 ]

В машинах-автоматах с жесткими связями время рабочего цикла практически постоянно и от длительности работы машины не зависит. Следовательно, постоянными являются технологическая и цикловая производительность машины. В машинах сгидравлическими и пневматическими исполнительными механизмами колебания времени рабочего цикла более значительны, так как свойства рабочего телг (масла, воздуха) зависят от температуры и других факторов.

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: