 |
Фундаментальные взаимодействия и их формализация
|
|
|
|
· Существование материального объекта предполагает нахождение его в состоянии движения и взаимодействия. Движение и взаимодействие взаимно дополняют друг друга.
· Движение и взаимодействие являются способом существования материи.
· Основные (внешние) формы движения материи – это механическая, физическая, химическая, биологическая, социальная формы.
· Любая форма движения в ходе соответствующего анализа сводится к проявлению тех или иных фундаментальных взаимодействий материи (гравитационного, электромагнитного, сильного и слабого).
· Взаимодействие любого типа обязательно предполагает наличие передающей среды, иначе говоря, физического поля.
· Количественной мерой фундаментального взаимодействия (с позиций квантовой теории поля) является заряд как некая обобщенная характеристика.
Уравнения Гамильтона
где t – время;
N – число степеней свободы
qi и pi – обобщенные координаты и обобщенные импульсы рассматриваемой механической системы (их совокупность называют каноническими переменными);
H (qi, pi, t) – функция Гамильтона, равная (в случае независимости связей между элементами системы от времени и консервативности действующих сил) сумме кинетической и потенциальной энергий системы, т.е. ее полной энергии.
уравнения Лагранжа в случае действия на механическую систему только консервативных сил
, i = 1, 2,…, N
где L (
) – функция Лагранжа (или кинетический потенциал);
qi и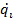 
– обобщенные координаты и обобщенные скорости для консервативной системы. Можно записать: L (
) = K () – U (qi),
где K () и U (qi) – соответственно кинетическая и потенциальная энергии системы.
Лагранжев подход является более универсальным, чем гамильтонов, в частности, он справедлив и в нелокальных теориях полей, в которых гамильтонов подход неприменим. Нелокальная теория поля рассматривается как обобщение квантовой теории поля, основанное на неточечности взаимодействия и введении специальных форм-факторов (при этом предполагается особое «размазывание» взаимодействия частиц по некоторой области пространства-времени).
|
|
|
Для каждого типа фундаментального взаимодействия выводится и записывается свой лагранжиан. Запись лагранжиана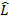 
достаточно сложна. Например, для электромагнитного взаимодействия частиц с электрическим зарядом Q 
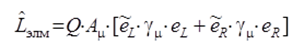где Аμ – операторная величина, описывающая векторное электромагнитное поле; μ = 0, 1, 2, 3; γμ − матрицы Дирака; 
и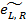 
– спинорные состояния электронов и позитронов с SU (2)-симметрией (L − «левые» и R − «правые» спиноры соответственно).
Диаграммы Фейнмана — наглядный и эффективный способ описания взаимодействия в квантовой теории поля. Правила построения диаграмм:
• сплошной линией со стрелкой (указывает направление распространения) обозначают свободную частицу вещества (например, электрон);
• волнистой линией обозначают виртуальную частицу – квант поля;
• точками (1, 2, …) обозначают акты взаимодействия частиц.
Ось времени направляют слева направо, а количество актов взаимодействия частиц определяет порядок диаграммы. Фейнмановская диаграмма позволяет с помощью определенных математических правил вычислить вероятность рассматриваемого квантового перехода. Вклад каждой вершины (точки) диаграммы в амплитуду процесса (квадрат амплитуды определяет вероятность процесса) пропорционален константе связи тех частиц (или полей), линии которых сходятся в вершине.
константой связи является электрический заряд е
Эффект Комптона
диаграмма 2-го порядка, она отражает рассеяние фотона на электроне: вначале присутствуют свободные электрон е и фотон γ, которые в точке 1 встречаются, происходит поглощение фотона электроном и переход последнего в промежуточное состояние (1 – 2); в точке 2 электрон испускает новый фотон γ' и переходит в новое состояние е '.
|
|
|
Акт электромагнитного взаимодействия электронов.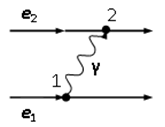 
диаграмма 2-го порядка, отражает процесс обмена фотоном между двумя электронами: один электрон е1 в точке 1 испускает фотон γ, который затем в точке 2 поглощается вторым электроном е2.
Слабое взаимодействие
-Обладает самым малым радиусом действия r ≈ 
м
-очень низкой интенсивностью (I ≈ 
отн. ед.), что проявляется в относительной медлительности связанных с ним процессов.
Свойства и характеристики слабого взаимодействия
· длина свободного пробега частицы в веществе. Так, сильно взаимодействующие частицы – адроны – можно задержать стальной плитой толщиной ~ (3…5) 
м, а нейтрино, участвующее лишь в слабых взаимодействиях, проходит без столкновений через стальную плиту воображаемой толщиной ~ 
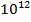м.
· При энергии в 1 ГэВ процесс, обусловленный сильным взаимодействием, идет ~ 
c, электромагнитным взаимо-действием ~ 
c, слабым взаимодействием ~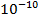 
с.
· слабое взаимодействие играет очень важную роль в природе: оно ответственно: а) за β±-распад ядер (иначе говоря, за распад нейтрона и протона); б) за распад многих других частиц (мезонов, гиперонов).
теория β-распада: Ферми положил в основу своей теории взаимодействие двух слабых токов не на расстоянии, т. е. путем обмена виртуальной частицей – квантом поля, а контактно. Это взаимодействие между четырьмя фермионными полями (или фермионами р, n, е, ν) в современных обозначениях отражается формулой: 
где 
– постоянная Ферми, Ток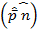 
, переводящий нейтрон в протон, - нуклонный ток, а ток 
– лептонным током.
слабый ток меняет заряды частиц: он превращает нейтрон в положительный протон, нейтрино – в электрон, а электромагнитный ток оставляет протон протоном, электрон электроном. В связи с последним свойством слабые ток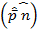и и стали называть также заряженными
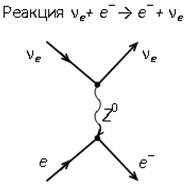
Теория электрослабого взаимодействия Глэшоу, Вайнберг и Салам Взаимодействие не является контактным, а происходит путем обмена промежуточными векторными бозонами (
, 
, 
– тяжелыми частицами со спином š = 1). Три промежуточных бозона и фотон являются квантами калибровочных векторных полей, выступающими при больших передачах импульсов (при энергии ~ 500 ГэВ) совершенно равноправно.
|
|
|
|
|
|
