Фундаментальные законы сохранения для изолированных систем

- закон сохранения энергии, т.е. E = K + U = const (в механике равенство выполняется в отсутствие неконсервативных сил);

- закон сохранения импульса, т.е. ;

- закон сохранения момента импульса, т.е. ;

-закон сохранения электрического заряда, т.е. .

К строгим законам сохранения в микромире относят:

· закон сохранения барионного заряда, выполняющийся во всех видах взаимодействий, и которому соответствует правило отбора Δ B = 0;

· закон сохранения лептонного заряда и выполнение соответствующего правила отбора Δ L = 0.

К нестрогим законам сохранения относят:

· закон сохранения изотопического спина (т.е. должно соблюдаться Δ I = 0), который выполняется только при сильном взаимодействии;

· законы сохранения «аромата», которые выполняются при сильном и электромагнитном взаимодействиях, но нарушаются в слабых взаимодействиях.

Если известны свойства (параметры) симметрии некоторой физической системы, то, как правило, можно установить для нее законы сохранения, и наоборот.

Теорема Нетер: Для физической системы (уравнения движения которой имеют форму системы диф-ных уравнений и могут быть получены из вариационного принципа механики) каждому, непрерывно зависящему от одного параметра, преобразованию, оставляющему инвариантным действие (D), соответствует закон сохранения.

Согласно теореме Нётер, каждому преобразованию, при котором действие D не изменяется (D=const, δD=0), соответствует дифференциальный закон сохранения; интегрирование уравнения этого закона приводит к интегральному закону сохранения. Согласно теореме Нетер:

• из инвариантности относительно сдвига во времени следует закон сохранения энергии;

• из инвариантности относительно пространственных сдвигов (это обусловлено однородностью самого пространства) следует закон сохранения импульса;

• из инвариантности относительно пространственного вращения (это обусловлено изотропностью пространства) следует закон сохранения момента импульса.

Теорема Нётер распространяется на пространственно-временные симметрии и внутренние симметрии, обусловленные внутренними свойствами элементарных частиц

Хаотические системы: Системы, предрасположенные к изменению своей структуры (сложности), принято называть динамическими.

Динамические системы подразделяются на:

•устойчивые системы и неустойчивые системы.

Крайним случаем неустойчивых динамических систем следует рассматривать хаотические системы, для которых описание в терминах траекторий становится недостаточным, поскольку траектории таких систем, первоначально сколь угодно близкие, со временем экспоненциально расходятся. Системы, допускающие несводимое вероятностное описание- хаотические.

Динамические системы в соответствии с подходом А. Пуанкаре подразделяют на:

•интегрируемые системы, для которых удается исключить взаимодействие частей системы;

•неинтегрируемые системы, для которых не удается исключить взаимодействие частей системы.

Интегрируемые системы становятся по существу изоморфными системами свободных частиц, т.е. все движения таких систем изоморфны (подобны по форме) движению свободных (невзаимодействующих) частиц; а простейшая форма их уравнений движения позволяет путем интегрирования получить в явном виде траектории частиц.

Порядок и беспорядок

В действительности равновесие соответствует только вполне конкретной ситуации. Если наложить извне ограничения (например, будем нагревать одну границу системы и охлаждать другую), то можно помешать системе достичь равновесия. Однако система может перейти в не зависящее от времени стационарное состояние, в котором энтропия системы не изменяется. Изменение энтропии со временем можно разделить на вклады двух типов: а) поток энтропии , зависящий от обмена системы с окружающей средой, и б) производство энтропии σ, обусловленное необратимыми процессами внутри системы. 2-ое начало термодинамики требует, чтобы производство энтропии было положительным или обращалось в нуль при достижении системой равновесия. На поток 2-ое начало не налагает никаких условий.

Вывод. В стационарном состоянии положительное производство энтропии (σ > 0) компенсируется отрицательным потоком энтропии (), а активность, производящая энтропию σ, постоянно поддерживается за счет обмена с окружающей средой. Равновесие соответствует частному случаю, когда и поток , и производство σ → 0.

Эффект Соре: Два сосуда одинакового объема V, соединены трубкой и заполнены смесью двух газов: водород и азот. Когда система находится в равновесии в обоих сосудах - однородную смесь. Выведем систему из равновесия - будем нагревать правый сосуд, и поддерживать наложенную на систему связь (Q). Т. о, мы накладываем на систему отрицательный поток энтропии. Вместе с потоком тепла происходит процесс разделения двух газов. Когда система достигает своего стационарного состояния: в горячем сосуде (Т 2) окажется больше молекул водорода (H2), а в холодном сосуде (Т 1) – больше молекул азота (N2); и разность концентраций смеси в сосудах пропорциональна разности температур, т.е. (n 1 – n 2) ~ (T 2 – T 1). Вывод. Активность системы, обуславливающая производство энтропии, связана не только с выравниванием температур, но и с созданием особого «порядка». «Беспорядок», порождаемый тепловым потоком, следует рассматривать как цену за возможность создать порядок, который в приведенном примере представляет обеспечение различия в составе газовой смеси в сосудах.

Диссипативные структуры – структуры, существующие постольку, поскольку система диссипирует (рассеивает) свою энергию и=> производит энтропию.

Диссипативные структуры можно рассматривать как пространственные, временные или пространственно-временные структуры, которые возникают вдали от состояния равновесия в нелинейной области (среде) при критических (пороговых) значениях параметров системы.

Неустойчивость Бенара: в тонком слое жидкости поддерживается внешним образом разность температур между нижней, подогреваемой, поверхностью (Т 2) и верхней свободной поверхностью, которая находится при комнатной температуре (Т 1).При малой разности температур Δ Т (вблизи равновесия), перенос тепла осуществляется за счет теплопроводности, т.е. столкновений между молекулами в ходе их хаотического движения. Выше определенного порога разности температур Δ Т > Δ Т пор тепло начинает переноситься за счет конвекции, т.е. здесь молекулы, наряду с хаотическими движениями, участвуют в коллективных движениях, соответствующих своеобразным вихрям, разделяющим слой жидкости на регулярные ячейки – «ячейки Бенара». Сами вихри также называют вихрями Бенара. Вблизи равновесия жидкость – однородна. Но когда наступает неустойчивость Бенара, ситуация – изменяется: в одной точке пространства молекулы поднимаются, а в другой – опускаются, как по команде, так как они уже вовлечены в конвективное движение. Т.о, в результате одной единственной тепловой связи, наложенной на слой жидкости, одни и те же молекулы, взаимодействующие посредством случайных столкновений, могут начать когерентное коллективное движение.

Структуры Тьюринга -химические диссипативные структуры, нарушающие пространственную симметрию. А. Тьюринг выдвинул гипотезу о том, что взаимодействие между нелинейными химическими реакциями и диффузией может приводить к образованию пространственных структур, отличающихся концентрациями реагентов. В конце 1980-х годов было проведено моделирование химически-реагирующей системы. Результаты моделирования позволили проследить переход от пространственно однородной системы к пространственно структурированным состояниям по мере того, как система удаляется от равновесия. По мере изменения концентрации реагентов смеси, сначала появляется структура «пчелиные соты», затем – «полосы» и наконец – «гексагональная структура». Белые зоны соответствуют максимальной концентрации реагентов. Каждая из структур обладает вполне определенной областью устойчивости.

 

Эволюцию динамических систем во времени удобно анализировать в фазовом пространстве. Фазовое пространство – абстрактное пространство с числом измерений, равным числу переменных, полностью характеризующих состояние (положение) рассматриваемой системы.

Пример: Линейный гармонический осциллятор:

Имеет одну степень свободы, а размерность его фазового пространства равна двум. Фазовое пространство в этом случае представляет плоскость, на которой эволюция осциллятора отражается через непрерывное задание его координаты и скорости (или импульса). Точка, изображающая состояние осциллятора на фазовой плоскости, будет двигаться по так называемой фазовой траектории.

В случае идеального осциллятора (колебания которого не затухают) в зависимости от начальных условий (при t0 = 0) будем иметь на фазовой плоскости систему концентрических эллипсов с общим уравнением:

В случае реального осциллятора (колебания затухают) при любых начальных условиях () фазовая траектория представляет собой некоторую закручивающуюся спираль, которая оканчивается в одной точке, отвечающей покою в положении равновесия. Эта точка О, или аттрактор, как бы притягивает к себе со временем все фазовые траектории и является обобщением понятия «равновесие».

Аттрактор – это конечное состояние эволюции диссипативной системы.

Пример: «Химические часы»: эволюционирует к устойчивому периодическому режиму. Эта структура представляет собой химически реактивный раствор двух компонент, в котором развивается реакция Белоусова-Жаботинского. Здесь реакционная среда (химраствор) периодически изменяет цвет: при подходящих условиях жидкость становится с периодом ~ 1 мин. то красной, то синей (в зависимости от доминирования той или иной компоненты). 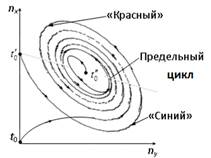Аттрактором становится линия на соответствующей фазовой плоскости, координатными осями на которой являются концентрации химических реагентов (nx, ny). Такой аттрактор описывает периодическое во времени изменение концентрации веществ в системе и также может рассматриваться как предельный цикл при любых начальных условиях ().

Странные аттракторы

В случае хаотического движения динамической системы фазовые траектории с близкими начальными параметрами состояния – быстро расходятся, а потом хаотически перемешиваются, так как они могут удаляться только до некоторого предела из-за ограниченности области изменений координат и скоростей (последнее определяется возможностями самой системы). В связи с этим фазовые траектории образуют складки внутри фазового пространства и оказываются достаточно близко друг к другу. Так возникает область фазового пространства, заполненная хаотическими траекториями, называемая странным аттрактором. 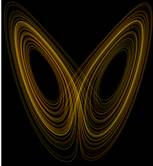По геометрическим формам странный аттрактор представляет сложную поверхность, ограничивающую некоторый объем в фазовом пространстве. Случайные воздействия на систему вызывают хаотические движения и появление сложных, «замысловатых» траекторий в результате растяжений и складываний в фазовом пространстве. На рис. представлен «странный аттрактор Э. Лоренца», полученный в ходе моделирования на компьютере конвективных потоков в земной атмосфере.

Важнейшим свойством странных аттракторов является их фрактальность.

Фракталы – это объекты с дробной размерностью, проявляющие по мере своего развития все большое число мелких деталей.

Пример: Канторовское множество: Возьмем единичный отрезок (0 - 1), разделим его на три равные части и удалим среднюю часть; повторим ту же операцию с оставшимися отрезками-частями много раз, получится бесконечное множество «микроотрезков», которые уже невозможно охарактеризовать их длинами. После п -ой типовой операции полное число полученных отрезков будет: N = , а длина каждого из них: l = 1/ . Размерность d канторовского множества при N → ∞ и l → 0 определяется из общей формулы: N = , т.е. в нашем случае: = равна d = log 2 ≈ 0,65. Т.о, в общем случае канторовское множество имеет дробную размерность в диапазоне: 0 < d < 1.

Хаос порождает фракталы, фазовая траектория фракталов обладает самоподобием, т.е. при выделении двух близких точек на фазовой траектории и последующем увеличении масштаба – траектория между этими точками окажется столь же хаотической, как и в целом. Выводы: странные аттракторы порождают такие типы поведения системы, которые невозможно однозначно ни предсказать, ни воспроизвести. В любой области, занимаемой фрактальным аттрактором, сколь бы мала она ни была, обнаруживается одна и та же сложная структура. В результате начальные условия, сколь угодно близкие, но не совпадающие полностью, порождают разные варианты эволюции системы. Малейшее различие в начальных условиях или малейшее возмущение (флуктуация) – не затухает, а усиливается аттрактором.

Бифуркацией называется скачкообразное изменение состояния системы.

Неустойчивость и неравновесность определяют развитие системы. В критическом состоянии (на момент бифуркации) флуктуации достигают такой силы, что существующая к этому моменту организация – разрушается - происходит быстрый переход – скачок диссипативной системы на новый и более высокий уровень упорядоченности. Момент перехода определяется свойствами системы и уровнем флуктуаций в ней. Параметры состояния системы, изменения которых приводит к качественной перестройке системы, называются управляющими параметрами.

Последовательность бифуркаций, возникающая при углублении неравновесности в системе, все время меняется => имеем много решений

Попав в область аттрактора, точка (выбранное наугад решение) будет «блуждать» там, и только через большой промежуток времени приблизится к какой-то его точке. При этом поведение системы, отвечающее такой точке, будет сильно зависеть от начальных условий.

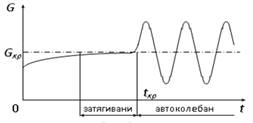При медленном изменении параметра управления возможно наблюдение «затягивания потери устойчивости». После прохождения параметра управления G через бифуркационное значение G кр, соответствующее мягкому возникновению автоколебаний, система остается в окрестности неустойчивого состояния некоторое время, за которое параметр меняется на конечную величину. После чего система скачком переходит в момент бифуркации t кр в автоколебательный режим.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: