 |
Теория подобия тепловых процессов
|
|
|
|
Николаев 2008
УДК 519.876.5:536.2
ББК 22.1: 31.31
Л42
Рекомендован Методическим советом НУК
Лейбович Л.И.
Л42 Практикум по математическому моделированию и оптимизации процессов теплообмена. - Николаев: НУК, 2008. - 44 с.
Практикум составлен в соответствии с программой дисциплины "Математическое моделирование и оптимизация процессов теплообмена". В этом издании использованы основные понятия и определения, приведенные в учебном пособии Дымо Б.В. "Практика с тепло - массообмена". Также даны дополнительные расчетные зависимости, контрольные задачи и примеры их решения.
Практикум предназначен для студентов специальностей направления 0905 "Энергетика". Может быть полезным аспирантам, научным и инженерно - техническим работникам в области энергетики.
УДК 519.876.5:536.2
ББК 22.1: 31.31
© Лейбович Л.И., 2008
© Издательство НУК, 2008
ПРЕДИСЛОВИЕ
Усовершенствование теплообменного энергетического оснащения в настоящее время в значительной мере проводится на основе модельных исследований. В условиях модели наиболее просто и мобильно можно исследовать влияние геометрических и режимных параметров, оптимизировать конструкции, а также проверить новые эффективные решения. Часто в натурных условиях такие исследования становятся чрезвычайно сложными и даже невозможными. В данное время ни одно энергетическое устройство не проектируется, если в той или другой мере не пройдена стадия модельного исследования. Специалистам по теплообменному энергетическому оснащению необходимы знания в области математического моделирования для решения подобных задач моделирования и оптимизации, поскольку для многих процессов теплообмена строгое физическое моделирование невозможно или сложно.
|
|
|
Пособие базируется на предшествующем изучении студентами курсов: высшая математика и основы программирования; физика (механика, теплота и молекулярная физика, законы сохранения тепла и массы и прочее); техническая термодинамика, гидрогазодинамика и теплообмен.
А также на базе достаточных знаний у студентов символьного и численного решения разнообразных задач в пакете прикладных программ Mathcad (версии 8-14).
Пособие состоит из разделов соответственно темам дисциплины "Математическое моделирование и оптимизация процессов теплообмена". Каждый раздел содержит в себе примеры решение типичных задач, а также задачи, которые охватывают широкий круг практических вопросов, которые встречаются при решении проблем современной теплоэнергетики. Такое построение удобно для самостоятельной работы студентов дневной и заочной форм обучения, а также проведение лабораторных и практических занятий.
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
r - радиус, м;
d - диаметр, м;
l - линейный размер, м;
δ - толщина, м;
τ- время, с;
T - температура, К;
Δ Т - температурный напор, К;
Θ - безразмерная температура.
Р - давление, Па;
G - массовый расход жидкости, кг/с;
w - скорость, м/с;
ср - теплоемкость, кДж/(кг*К);
Q - тепловой поток, Вт;
q - плотность теплового потока, Вт/м2;
α - коэффициент теплоотдачи, Вт/ (м2.К);
k - коэффициент теплопередачи, Вт/ (м2.К);
ε - степень черноты тела;
λ - коэффициент теплопроводности, Вт/ (м.К);
ρ - плотность, кг/м3;
a - коэффициент температуропроводности, м2/с;
μ - динамический коэффициент вязкости, Па.с; или корень
характеристического уравнения;
ν - кинематический коэффициент вязкости, м2/с;
β - температурный коэффициент объемного расширения, К-1;
g - ускорение свободного падения, м2/с;
х, в, z - координаты, м.
|
|
|
1. ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ БАЗ
ДАННЫХ ФИЗИЧЕСКИХ ПАРАМЕТРОВ
Расчеты процессов теплообмена в энергетическом оборудовании требуют постоянного выбора значений физических свойств сред, которые принимают участие в процессе теплообмена. Как правило, эти величины зависят от температуры и давления среды. Постоянная работа с таблицами физических свойств сред и ручное введение выбранных значений усложняет работу с прикладными программами на ЭВМ. Это обосновывает целесообразность перевода табличных данных в форму, удобную к использованию в расчетах теплообменных процессов на ЭВМ. В Mathcad существуют несколько методов интерполяции и экстраполяции. Для большинства инженерных расчетов теплотехнических процессов наиболее наглядным методом, который обеспечивает достаточную точность расчетов, есть метод кубической сплайновой интерполяции - соединение точек с использованием кубических линий. Особенность кубической сплайновой интерполяции базы данных следующая - данные в столбцах матрицы должны располагаться в порядке возрастания.
Пример 1.1. Выполнить кубическую сплайновую интерполяцию физических свойств воздуха (коэффициент теплопроводности λ, кинема-тический коэффициент вязкости ν, число Прандтля Pr) в диапазоне температур Т = 273...313 К. Выполнить вычисления указанных параметров для значения температур воздух 283 и 323 К.
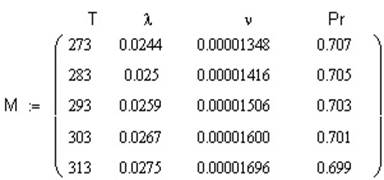Решение. Из табл. 2Д приложений пособия [2] формируем матрицу базы данных физических свойств воздух в следующем виде:
Каждый столбец вышеприведенной матрицы представим в виде векторов:
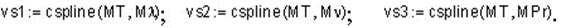Определим векторы коэффициентов кубического сплайна рассмотренных физических величин:
Определяем функции для расчета интерполяционных значений:
Выполним проверку правильности записи программы для интерполяции физических свойств воздуха. Для этого зададим, например, значения температуры воздух внутри рассмотренного диапазона (Т 1 = 283 К). Потом вычислим значения функций Fk 1(T 1), Fk 2(T 1) и Fk 3(T 1) для указанной температуры
Полученные результаты целиком совпадают с табличными данными.
Выполним проверку возможности экстраполяции. Для этого зададим значения температуры воздух за пределами рассмотренного диапазона температур. Например, пусть это значения температуры будет Т 2 = 323 К. Потом вычислим значения функций Fk 1(T 2), Fk 2(T 2) и Fk3 (T 2) для указанной температуры:
|
|
|
Сравнивая значения с табличными данными (см. табл. 2Д [2]) можно сделать вывод об удовлетворительной степени экстраполяции по данному методу.
ЗАДАЧИ
Задача 1.1. Выполнить кубическую сплайнову интерполяцию физических свойств вещества (плотность ρ, теплоемкость ср, динамический коэффициент вязкости μ) в диапазоне температур Т приведенных в колонке 3 табл.1.1. Выполнить вычисления указанных физических свойств вещества для температур, указаных в табл. 1.1 (колонки 4 и 5).
Таблица 1.1.
| № | Вещество и источник базы данных его физических свойств | Диапазон температур Т, К | Значение температур для проверки Т, К | |
| интерполяция | экстраполяция | |||
| Воздух (табл. 2Д [2]) | 223...313 | |||
| Воздух (табл. 2Д [2]) | 313...393 | |||
| Воздух (табл. 2Д [2]) | 393...523 | |||
| Воздух (табл. 2Д [2]) | 523...723 | |||
| Вода на линии насыщения (табл. 3Д [2]) | 273...323 | |||
| Вода на линии насыщения (табл. 3Д [2]) | 323...373 | |||
| Вода на линии насыщения (табл. 3Д [2]) | 373...423 | |||
| Вода на линии насыщения (табл. 3Д [2]) | 423...523 | |||
| Водяной пар на линии насыщения (табл. 4Д [2]) | 373...423 | |||
| Водяной пар на линии насыщения (табл. 4Д [2]) | 423...523 | |||
| Дымовые газы (табл. 5Д [2]) | 373...773 | |||
| Дымовые газы (табл. 5Д [2]) | 773...1473 |
Задача 1.2. Выполнить кубическую сплайновою интерполяцию физических свойств веществ (коэффициент теплопроводности λ, кинематический коэффициент вязкости ν, число Прандтля Pr) в диапазоне температур Т, приведенных в колонке 3 табл. 1.2. Выполнить вычисления указанных физических свойств вещества для температур, обозначенных в табл. 1.2 (колонки 4 и 5).
Таблица 1.2.
| № | Вещество и источник базы данных его физических свойств | Диапазон температур Т, К | Значение температур для проверки Т, К | |
| интерполяция | экстраполяция | |||
| Воздух (табл. 2Д [2]) | 223...323 | |||
| Воздух (табл. 2Д [2]) | 313...383 | |||
| Воздух (табл. 2Д [2]) | 373...503 | |||
| Воздух (табл. 2Д [2]) | 523...723 | |||
| Вода на линии насы-щения (табл. 3Д [2]) | 273...333 | |||
| Вода на линии насы-щения (табл. 3Д [2]) | 303...363 | |||
| Вода на линии насы-щения (табл. 3Д [2]) | 343...423 | |||
| Вода на линии насы-щения (талб. 3Д [2]) | 493...523 | |||
| Водяной пар на линии насыщения (табл. 4Д [2]) | 373...443 | |||
| Водяной пар на линии насыщения (табл. 4Д [2]) | 423... 523 | |||
| Дымовые газы (табл. 5Д [2]) | 373...773 | |||
| Дымовые гази (табл.5Д [2]) | 773...473 |
|
|
|
ТЕОРИЯ ПОДОБИЯ ТЕПЛОВЫХ ПРОЦЕССОВ
Теория подобия тепловых процессов играет важную роль в математическом моделировании и оптимизации процессов теплообмена. На основе чисел теплового и гидродинамического сходства рассчитываются условия моделирования или формируются критериальные уравнения, которые описывают процессы теплообмена. Ниже на приведенных примерах показаны принципы использования теории подобия в моделировании процессов теплообмена
Пример 2.1. На экспериментальной установке исследовался теплообмен между поверхностью горизонтально расположенной трубы и свободным потоком воздуха. Внешний диаметр трубы d = 0,045 г. Температура воздуха, которая находится вдали от поверхности трубы, Т в = 293 К. В экспериментах получены следующие данные за коэффициентом теплоотдачи α, используя которые найти критериальное уравнение для определения чисел Нуссельта:
Δ Т, К 20 40 60 80 100
α, Вт/(м2. К) 6,00 7,10 7,90 8,45 8,97,
где ΔТ – разность температур между стенкой и воздухом.
Решение. Согласно табл. 7.1. [2] критериальне уравнению имеет вид
Nu = c. (Gr . Pr)n. (Pr / Prс)m,
где Nu = α d/ λ; Gr = g βΔ Тd 3/ν2, Pr = ν/ a. Значение чисел Грасгофа Gr и Прандтля Pr рассчитываются по температуре воздуха вдали от исследуемой трубы. Значение числа Прандтля Pr с - по температуре стенки. Как правило, значение коэффициента равняется m = 0,25.
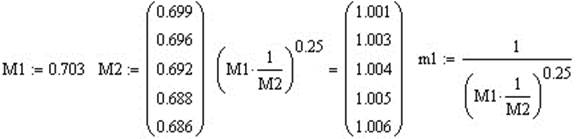Определим влияние отношения (Pr / Pr с) m на значение числа Нуссельта, на- ходя значение чисел Прандтля для соответствующих температур (табл.2Д [2]):
Физические свойства воздуха при температуре Т = 293 К имеют значение: λ =0.0259 Вт/ (м.К); ν =15.06. 10-6 м2/с; а =21.4.10-6 м2/с; β=1/273 К-1. Введем следующие обозначения физических величин для выполнения расчетов в пакете программ Mathcad
Определим значения чисел Нуссельта, произведения чисел Нуссельта на 1 /( Pr / Pr с)0.25 и логарифмы произведений этих величин:
Определим значения комплекса G r. Pr и их логарифмов:
|
|
|
Строим график зависимости логарифмов этих величин (рис.2.1).
Рис.2.1. Зависимость log(Nu/(Pr/Prc)0.25) от log (Gr.Pr).
По тангенсу угла наклона полученной прямой к оси абсцисс определяем показатель степени n = 0,246. А затем находим значение постоянной с по следующей зависимости с = Nu . (Pr/Prc) 0.25 / Gr 0.246.
Пример 2.2. Резервуар для сохранения сжиженного пропана представляет собой бетонный толстостенный сосуд с внутренним диаметром d v = 6,0 м и толщиной стенки δc = 0,300 м. Начальная температура стенки Т с = 283К. Хранилище заполняется редким пропаном с температурой Т п = 231 К. Предполагается, что через τ =10 часов на поверхности резервуара со стороны прилегающего грунта температура стенки достигнет значение Т с1 = 273 К. Коэффициент теплоотдачи к сжиженному пропану в процессе теплообмена в резервуаре и в модели
α = 280 Вт/(м2. К). Коэффициент теплопроводности можно считать одинаковымдлягрунта и бетона λ = 1,28 Вт/ (г. К).
Определить параметры модели для натурных исследований процессов теплообмена в таких резервуарах методом математического моделирования, при которых температура на внешней поверхности модели резервуара со стороны грунта достигает значение Т с1 = 273 Кза τ г = 1 ч.
Решение. Подобие полей температур в стенках резервуара и модели будет иметь место при равенстве чисел подобия Био Bi = Bi м и Фурье Fo = Fo м.
На основании равенства чисел Фурье для резервуара и модели можно записать: (a . τ) / δc2 = (a . τг) / δcм2
или ______ _____
δcг = δc √ (τг / τ) = 0,3 √ (1/10) = 0,095 м.
Число Био для резервуара и модели в этом случае можно модифицировать, заменив коэффициент теплоотдачи от поверхности стенки к сжиженному пропану на коэффициент теплопередачи от грунта к сжиженному пропану через бетонную стенку. В таком случае равенство чисел Био для резервуара и модели будет иметь вид:
k . δc = k м . δcм.
Произведение коэффициента теплопередачи через цилиндрическую стенку [3] на толщину стенки можно записать:
где d vи d n– внутренний и внешний диаметр резервуара (модели), м; db - диаметр цилиндрического пласта земли, на котором практически нет изме-нения температуры земли, м.
Для расчетов в пакете программ Mathcad введем следующие исходные данные задав значения внутреннего диаметра модели dn1= 1,1
.
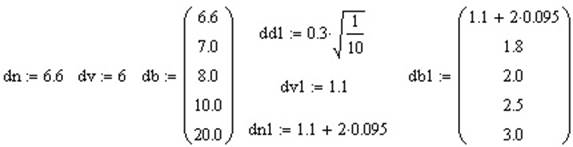Значение комплекса k . δc для резервуара:
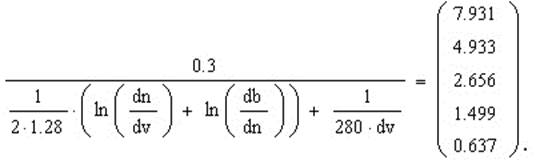
Значение комплекса k м . δcмдля модели:
Для выбора окончательных параметров модели построим графики зависимостей k . δc = f(db) и k м . δcм = f(db1).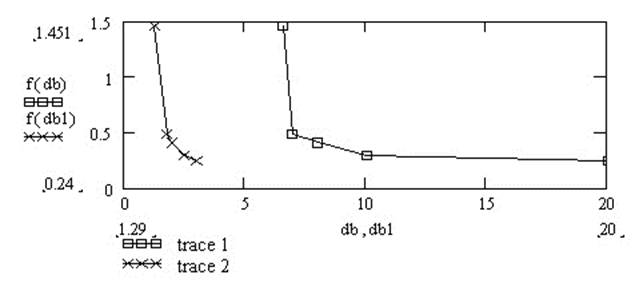 
Рис. 2.2. Зависимость чисел Био для резервуара и модели.
Анализ результатов моделирования показывает, что обеспечить доста-точно близкие плотности теплового потока на модели можно в случае обес-печения одинаковых условий внешнего теплообмена в резервуаре и модели. Для этого необходимо иметь соотношение диаметров db/dv = 1,6...1,8.
ЗАДАЧИ
Задача 2.1. В результате исследований теплообмена между водой и горизонтальной пластиной длиной l = 8 мпри температуре жидкости вдали от пластины Т ж = 303 К получили следующие экспериментальные данные (табл. 2.1).
Таблица 2.1.
| № | w, м/с | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| α, Вт/(м2 . К) | ||||||
| α, Вт/(м2. К) | ||||||
| α, Вт/(м2 . К) | ||||||
| α, Вт/(м2 . К) | ||||||
| α, Вт/(м2 . К) | ||||||
| α, Вт/(м2 . К) |
Рассчитать значения чисел Рейнольдса для заданного диапазона скоростей. На основании данных табл. 6.1. [2] определить режим течения жидкости и вид уравнения подобия для расчета среднего значения числа Нуссельта. Найти константу и показатель степени при числе Рейнольдса в избранном уравнении подобия.
Задача 2.2. На основе уравнения для расчета локальных значений чисел Нуссельта при свободном движении воздуха у нагретой вертикальной пластины Nu = 0,473 . (Gr . Pr) 0,25 определить значения этих чисел Нуссельта в следующих точках: x/l = 0,2; x/l =0,4; x/l = 0,6; x/l = 0,8 и x/l = 1,0. Исходные данные приведены в табл. 2.2.
Таблица 2.2.
| № | l, г | Т в, К | Т ж, К |
| 0,4 | |||
| 0,6 | |||
| 0,8 | |||
| 0,4 | |||
| 0,6 | |||
| 0,8 |
Задача 2.3.Для снижения потерь тепла из помещения его стены облицовывают пенопластом. Определить необходимую толщину пенопласта для обеспечения коэффициента теплопередачи от воздуха внутри помещения к внешнему воздуху не большее к = 1 Вт/ (м2 . К). Коэффициенты теплоотдачи внутри помещения αв = 6 Вт/(м2, К) и извне αн = 15 Вт/(м2. К). Исходные данные для расчета приведены в табл. 2.3.
Таблица 2.3.
| № | Материал стены | λ, Вт/(м . К) | Толщина стены l, м |
| Бетон | 1,28 | 0,10; 0,12; 0,14; 0,16; 0,18 | |
| Кирпич красный | 0,81 | 0,25; 0,375; 0,5; 0,625 | |
| Кирпич силикатный | 0,86 | 0,25; 0,375; 0,5; 0,625 | |
| Песчаник | 0,93 | 0,2; 0,4; 0,6 | |
| Камень «ракушняк» | 0,63 | 0,2; 0,4; 0,6 | |
| Шлакобетон | 0,70 | 0,2; 0,4; 0,6 |
Задача 2.4 При построении больших гидросооружений возникает необходимость в искусственном охлаждении плотин, так как теплота, которая выделяется, может привести к образованию трещин. При искусственном охлаждении плотин следует контролировать температуру в отдельных элементах плотины после заключения в них бетона через2, 5, 10 и 27 часов. Температурное поле в одном из элементов плотины получают опытным путем на модели. Коэффициент теплоотдачи в модели в n раз выше, чем коэффициент теплоотдачи в натуральных условиях. Физические характеристики материала модели и натурального образца одинаковые. Определить размеры модели, а также промежутки времени, в течении которых следует измерять температуру в ней, если натуральный образец представляет собой параллелепипед с сторонами l 1 х l 2 х l 3, м. Исходные данные для решения задачи 2.4. данные в табл. 2.4
Таблица 2.4.
| № | L1 | l2 | l3 | N |
| 2,0 | 2,0 | |||
| 2,2 | 2,2 | |||
| 2,4 | 2,4 | |||
| 2,6 | 2,6 | |||
| 2,8 | 2,8 | |||
| 3,0 | 3,0 |
|
|
|
