Главная | Обратная связь | Поможем написать вашу работу!

Нестационарная теплопроводность.

Основные соотношения для расчета нестационарной теплопроводности в телах разной формы приведенные в табл. 4.1 [2].

Пример 3.1. Для испытания на стойкость к образованию трещин бетонную плиту из гидротехнического бетона размерами l 1 х l 2 х l 3м умещают в камеру искусственного климата, температура в которой поддерживается постоянной T _в= const, K; коэффициент теплоотдачи от поверхности плиты к воздуху α_в= const, Вт/(м^2.К). Начальная температура бетона Т _б= const,К. Исходные данные приведены в табл. 3.1

Найти распределение температур по толщине плиты через промежуток

времени 0,5; 1,0; 3,0; 6,0 и 24 часапосле размещения плиты в испытательную камеру.

Таблица 3.1.

№	l₁	l₂	l₃	α_г	T_в	Т_б
	0,20	2,0	2,0

Решение. Поскольку толщина плиты на порядок меньшее двух других размеров, то в первом приближении плиту можно считать плоской безгра-ничной пластиной. Характерным размером пластины (табл. 2.4) при симметричном охлаждении есть половина ее толщины l = l _п /2 = 0,1м.

За справочниками определяются физические свойства бетона:

теплопроводность - λ_бт = 2,0 Вт/(г. К);

плотность - ρ_бт = 2400 кг/м³;

теплоемкость - с _б = 0,83кДж/(кг ^.К);

температуропроводность - а_б = 10^-6 м²/с.

Вычисляем значения чисел Био и Фурье

(значение времени в числе Фурье должны подставляться в секундах).

Решение сводиться к определению безразмерной температуры Θ, которое для безграничной пластины в произвольной точке с координатой х, в момент времени τможно вычислить по формуле

μ _n - n-й корень характеристического уравнения ctg μ = μ / Bi,

(значение μ _n - для n = 1, 2,...,6 определяются в зависимости от числа Био),

A_n = 2 (sin μ_n) / (μ_n + sin μ_{n *} cos μ_n).

Зная величину Θ, можно найти искомую размерную температуру Т(x,τ). Для инженерных расчетов достаточной точности можно использовать от одного до трех членов ряда для определения безразмерной температуры. Найдем значения корней характеристического уравнения используя метод кубической сплайновой интерполяции

Данные матрицы М в виде векторов имеет вид:

Определим коэффициенты кубического сплайна:

Определение функции для расчета интерполяционных значений с использованием кубического сплайна

Определим значения Fk_i(Bi) для значения критерия Bi =1,25

. Для удобства следующих вычислений введем обозначения

Вычислим значения коэффициентов А₁, А₂и А₃

Для значений l лежачих в границах 0...0,1 м введем значения безразмерной координаты j = y / l₁ и определим значения безразмерной температуры Θ для этих параметров

В результате расчетов получим

Распределение температур по толщине плиты приведено на рис. 3.1.

Рис. 3.1. Распределение температур по толщине плиты.

ЗАДАЧИ

3.1. Бункер с зерном (эффективный коэффициент теплопроводности λ_с = 0,163 Вт/(г.К), плотность ρ_с= 850 кг/м³, теплоемкость с_з = 840 Дж/(кг ^.К) имеет форму цилиндра радиусом r = r, м, и находиться в помещении с температурой воздуха T _в= T _в,К. Начальная температура зерна равняется температуре воздуха. В результате биологических процессов в зерне выделяется теплота в количества q _з = q _з,Вт/м³. Коэффициент теплоотдачи от поверхности бункера к воздуху α_в =α_в, Вт/(м^2.К). Коэффициент температуропроводности зерна a_z = 0,00000023 м²/с.

Считая приблизительно бункер неограниченным цилиндром, определить температуру его оси и поверхности через 15 часов. При решении применить метод суперпозиций. Исходные данные для решения задачи приведенны в табл. 3.2.

Таблица 3.2.

№ r,г T _в _,К q_з,Вт/м³ α_у, Вт/(м^2.К)

2,0 2,5 6,0

2,2 2,5 6,1

2,4 2,6 6,2

2,6 2,6 6,3

2,8 2,8 6,4

2,9 2,8 6,5

3,0 2,7 6,7

3,2 2,6 6,8

3,4 2,8 6,9

Задача 3.2. При определении коэффициента температуропроводности а теплоизоляционных материалов используется прибор, который представляет собою шар из исследуемого материала, внутри которого установленные две термопары: одна в центре, другая – на глубине r = 0,5 r _s радиуса шара. Шар нагревают до некоторой первоначальной температуре T _нач, а потом помещают в холодную среду, температура которой поддерживается постоянной T_c= const. В расчетах температуропроводности материала а принимают аналитическое решение задачи об охлаждении шара и данные одновременных значений показаний термопар в некоторый момент времени τ, которыйблизок регулярному режиму. На практике температуры регистрируются несколько раз, но в расчеты принимаются значение, при котором числа Фурье Fo > 0,3.

Определить коэффициенты температуропроводности материала описанным методом, если радиус пули r_s = 0,30 м, начальная температура материала пули T _s= T _s,K, температура охлаждающей среды T _c = T _c,K, показание термопар T _p1= T _p1,Kи T _p2= T _p2,Kпри времени охлаждения τ =20 мин. Теплоемкость материала c _s = 816 Дж/(кг ^.К), плотность материала ρ_s = 800 кг/м³(табл.3.2.).

Таблица 3.2.

№ T_s T_c T_p1 T_p2

275,0 274,0

275,0 273,8

276,0 275,0

276,2 275,6

275,9 275,0

276,0 275,0

277,0 276,0

282,9 282,0

276,0 275,0

4. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ (ЯВНЫЙ МЕТОД)

Методика численного решения задач нестационарной теплопроводности базируется на представлении рассматриваемого тела как совокупности узлов. Для каждого узла записывается баланс энергии, получая в итоге алгебраическое уравнение для расчета температуры в каждом узле. Для внутренних узлов тела формирование уравнение баланса энергии основывается на законе Фурье, а для узлов, расположенных на границе твердого тела и жидкости - используется уравнение Ньютона - Рихмана. В результате применения метода конечных различий выходит n алгебраических уравнений для n узлов рассматриваемого тела.

Пример 4.1. Большая толстая плита (коэффициент теплопроводности λ = 40 Вт/(м ^.К), коэффициент температуропроводности a = 3, 10^-5 м²/с) имеет постоянную температуру Т = 473 К. Поверхность плиты внезапно погружают в жидкость с температурой Т _ж = 373 К. Коэффициент конвективной теплоотдачи к жидкости от поверхности плиты - α = 500 Вт/м2 К.

Найти изменение температуры плиты на протяжении первой минуты после погружения в жидкость.

Решение. Плита разделяем на элементарные объемы с узлами, как показано на рис. 4.1. Нумерация узлов начинается от поверхности тела, граничащего с окружающей средой.

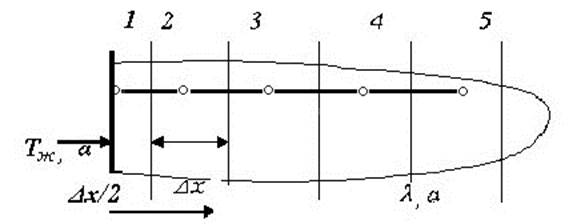
Рис. 4.1. Размещение элементарных объемов в рассматриваемом твердом теле.

Если учесть теплоемкость граничного с окружающей средой узла, то температура T (τ+Δτ) в этом граничном узле определяется соотношением

Т ₁^τ+Δτ= 2 Fo [ Т₂^τ + Bi ^. Т _ж ]+ [ 1 - 2 Fo - 2 Fo ^. Bi ] Т ₁^τ.

Все другие узлы являются внутренними. Поэтому для произвольного узла внутри твердого тела, обозначенного индексом i, применимое следующее соотношение

Т _i^τ+Δτ= Fo [ Т _i-1^τ+ Т _i+1^τ]+ [ 1 - 2 Fo ] Т _i ^τ.

Критерий стойкости для предельного узла Fo(1+ Bі) ≤ 0,5. И для внут-ренних узлов Fo ≤ 0,5.

Выберем удовлетворяющим этим критериям значения Fo = a ^.Δτ /(Δх)²= 0,25 и Bi= α Δ х / λ = 0,5. Поскольку число Био уже определено, то величина шага между узлами в твердом теле Δ х = λ / 2 α = 40/2 ^.500 = 0,04 м.

Шаг по времени ограничивается выбранной величиной числа Фурье

Δτ = (Δ х)^2/4. a = (0,04)^2/4 (3 ^,10^-5)= 13,33 c.

Теперь проведем расчет температур тела по неявному методу в узлах, которые отстоят один от другого на 0,04 м в моменты времени, чередующиеся с интервалом 13,33 с. Для решения задачи в пакете программ Mathcad введем следующие обозначения:

Расчет изменения температур при τ = Δτ:

Расчет изменения температур при τ = 2Δτ:

Расчет изменения температур при τ = 3Δτ:

Расчет изменения температур при τ = 4Δτ:

Расчет изменения температур при τ = 5Δτ:

Построим графики изменения температуры

в каждом узле рассматриваемого твердого

тела с течением времени. Для этого сведем

все результаты расчетов в матрицу.

На рис. 4.2. представлены графики изменения температуры в узлах рассматриваемого тела. Для получения болем плавных кривых не обходимо рассматриваемое твердое тело разить большее количество количество элементарных объемов.

Рис. 4.2. График изменения температуры внутри

твердого тела с течением времени.

ЗАДАЧИ

Задача 4.1. Поверхность толстой плиты имеет начальную температуру Т ₀ = 345 К. За счет радиационного обогрева поверхность приобретает быстро при находит температуру Т ₀₁ = Т ₀₁, К.. Найти время, за которое температура слоя тела на глубине 0,05 м достигнет значение Т01 + 15 К. Построить графики изменения температуры по глубине тела для найденного из условия стойкости шага по временем Δτ. Исходные данные приведенные в табл. 4.1.

Таблица 4.1.

Вариант
Т ₀₁,К
а,м²/с	2 ^.10^-6	3 ^.10^-6	4 ^.10^-6	5 ^.10^-6	7 ^.10^-6	8 ^,10^-6
λ = Вт/(м ^.К)

Задача 4.2. Детали из алюминия (диаметром d, длиной l, а = 97,5 м²/с и λ = 240 Вт/(м ^.К)) нужно нагреть к температуре Т = 473 К. Начальная темпе-ратура детали - Т ₀, К. Температура внутри камеры нагревания Т _ж = 673 К, коэффициент теплоотдачи от среды, которая греет, к детали - α =100 Вт/(м².К). Детали двигаются по конвейеру внутри камеры нагревания. Найти необхо-димую длину камеры, если скорость движения равняется w = w, м/с. Исходные данные для решения задачи приведенные в табл. 4.2.

Таблица 4.2.

№	d, м	L, м	w, м/с
	0,005	0,100	0,05	0,10	0,15	0,20
	0,008	0,090	0,05	0,10	0,15	0,20
	0,010	0,090	0,04	0,08	0,12	0,16
	0,012	0,080	0,04	0,08	0,12	0,16
	0,014	0,070	0,03	0,06	0,09	0,12
	0,016	0,070	0,03	0,06	0,09	0,12

Задача 4.3. Длинный прямоугольный стрежень (λ = 40 Вт(/м ^.К) и а = 3,10^-5 м²/с) имеет в начальный период времени постоянную температуру по всему объему - Т ₀ = 433 К. Внезапно температура неизолированных поверхностей снижается к значению T ₀₁, K. Найти значения температуры тела в точках согласно рисунку через 60, 120, 180, 240 и 300 с. Исходные данные приведенные в табл. 4.3.

Таблица 4.3.

T₀₁ l₁ l₂ № l₁, м l₂, м T₀₁, K

0,10 0,10

0,12 0,14

0,14 0,10

0,16 0,16

0,18 0,18

0,18 0,18

Задача 4.4. Длинный цилиндр из нержавеющий стали (диаметром d = d, м имеет в начальный период времени температуру Т ₀= Т ₀, K. Цилиндр изоли-рован по периферии. С одного торца есть подведение тепла, и температура этой торцовой поверхности равняется Т _т = Т _т, К. Найти значения температур в точках тела цилиндра, расположенных на расстоянии 0,01; 0,02; 0,04; 0,06 и 0,10 м от места подведения тепла, через периоды времени τ (табл. 4.4).

Таблица 4.4.

q Т _т Т ₀ № d, м τ, с Т₀, K Т_т, К

0,020

0,025

0,030

0,035

0,040

0,045

5. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ (НЕЯВНЫЙ МЕТОД)

Основной недостаток явного численного метода состоит в том, что разностное уравнение баланса энергии для каждого узла должно удовлетворять критерию стойкости. Неявный метод основан на том, что у уравнения баланса энергии температуры определяются в моменты времени τ +Δτ.

Пример 5.1. Решить пример 4.1. неявным числовым методом. Параметры плиты и окружающей среды такие же.

Решение. Разбивка плиты на элементарные объемы отвечает предшествующей задаче. Для граничного с окружающей средой елементарного объема 1 неявная форма разностного уравнения баланса энергии имеет вид

Т ₁^τ+Δτ[1+2 Fo (1+ Bi)] - 2 Fo [ Т ₂^τ+Δτ+ Bi Т _l^τ+Δτ] - Т ₁^τ=0.

Для других внутренних узлов, обозначенных индексом i, применимое следующее соотношение

[1 + 2 Fo ] Т _i^τ+Δτ- Fo [ Тt _i-1^{τ +Δτ}+ Тt _i+1^τ+Δτ]- Т _i^τ= 0.

Будем решать систему алгебраических уравнений методом обращенной матрицы, поэтому запишем все разностные уравнения баланса энергии в матричной форме: A1 ^.T = B.

Уравнение баланса энергии для граничного элементарного объема в матричной форме имеет вид

Т ₁^τ+Δτ[1+2 Fo (1+ Bi)] - 2 Fo Т ₂^τ+Δτ= 2 Fo Bi Т _l^τ+Δτ+ Т ₁^τ,

а для всех внутренних элементарных объемов уравнения баланса записывается следующим образом

- Fo Т _i-1^{τ +Δτ}+ [1 + 2 Fo ] Т _i^τ+Δτ- Fo Т_i ₊₁^τ+Δτ= Т _i ^τ.

Если принять значение шагов по координатам и времени как и в предшествующей задаче, то значение чисел Фурье и Био будут Fo = 0,25 и Bі = 0,5. Ограничим область решения 10 элементарными объемами. В таком случае используем 10 разностных уравнений баланса энергии:

узел 1: 1,75 Т ₁^τ+Δτ- 0,5 Т ₂^τ+Δτ= 25 + Т ₁^τ;

узел 2: - 0,25 Т ₁^τ+Δτ+ 1,5 Т ₂^τ+Δτ- 0,25 Т ₃^{τ +Δτ}= Т ₂^τ;

узел 3: - 0,25 Т ₂^τ+Δτ+ 1,5 Т ₃^τ+Δτ- 0,25 Т ₄^{τ +Δτ}= Т ₃^τ;

узел 4: - 0,25 Т ₃^τ+Δτ+ 1,5 Т ₄^τ+Δτ- 0,25 Т ₅^{τ +Δτ}= Т ₄^τ;

узел 5: - 0,25 Т ₄^τ+Δτ+ 1,5 Т ₅^τ+Δτ- 0,25 Т ₆^{τ +Δτ}= Т ₅^τ;

узел 6: - 0,25 Т ₅^τ+Δτ+ 1,5 Т ₆^τ+Δτ- 0,25 Т ₇^{τ +Δτ}= Т ₆^τ;

узел 7: - 0,25 Т ₆^τ+Δτ+ 1,5 Т ₇^τ+Δτ- 0,25 Т ₈^{τ +Δτ}= Т ₇^τ;

узел 8: - 0,25 Т ₇^τ+Δτ+ 1,5 Т ₈^τ+Δτ- 0,25 Т ₉^{τ +Δτ}= Т ₈^τ;

узел 9: - 0,25 Т ₈^τ+Δτ+ 1,5 Т ₉^τ+Δτ- 0,25 Т ₁₀^{τ +Δτ}= Т ₉^τ;

узел 10: - 0,25 Т ₉^τ+Δτ+ 1,5 Т ₁₀^τ+Δτ- 0,25 Т ₁₁^{τ +Δτ}= Т ₁₀^τ.

В эту систему уравнений входит значение температуры в узле 11. Температуру в узле 11 можно найти из граничного условия, которое требует, чтобы она оставалась равной начальной температуре 473 К, если время, на протяжении которого отыскивается решение, не слишком велико. Отметим, что на основании полученного решения предшествующей задачи температура в узле 5 практически не меняется в течении первой минуты. Поэтому, приняв температуру в узле 11 равной Т ₀, мы не получим серьозных ошибок. Тогда, уравнение энергии для узла 10 будет иметь вид:

- 0,25 Т ₉^τ+Δτ+ 1,5 Т ₁₀^τ+Δτ= 50 + Т ₁₀^τ.

Дальнейшее решение задачи будем выполнять в пакете программ Mathcad, используя матричный метод. Для этого все коэффициенты у систем и уравнений запишем в виде двух матриц:

Обращенная матрица имеет вид

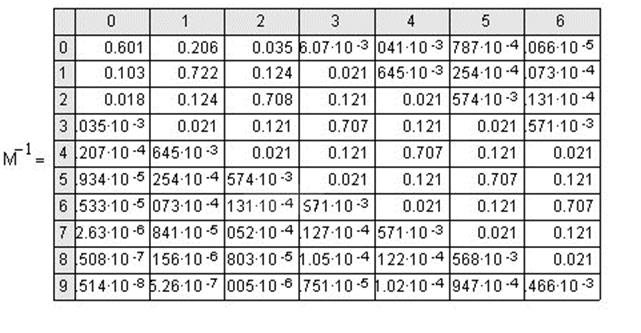
Для всех следующих шагов вычислений значения величин в матрице М^-1 остаются постоянными. Ниже приведенные результаты расчеты вычислений для значений времени 13,3; 26,6; 39,9; 43,2 и 56,5 с.

На основании проведеннях расчетов строим графики изменения температуры внутр. Рассматриваемого твердого тела (рис. 5.1).

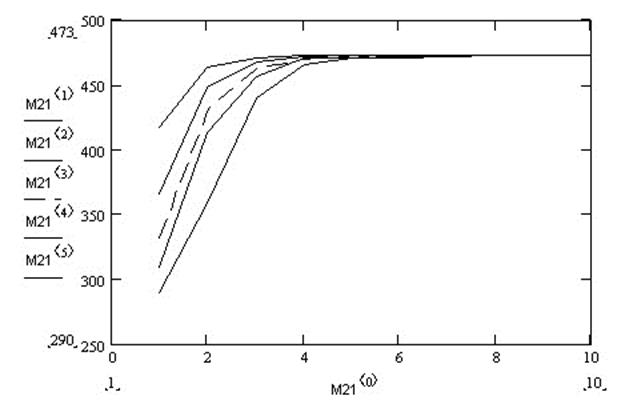
Рис. 5.1. Зависимость изменения температуры внутри твердого

тела по времени.

ЗАДАЧИ

Задача 5.1. Решить задачу 4.4. неявным методом.

Задача 5.2. Нагревается брус прямоугольного пересечения (коэффициент температуропроводносто а, м²/с; коэффициент теплопроводности λ, Вт/(м^. К)). Начальная температура бруса Т ₀= 300 К. Нагревание осуществляется с одной стороны и заканчиваются в тот момент, если на противоположной стороне бруса температура поверхности достигнет значение Т, К. На торцах бруса имеет место конвективний теплообмен (коэффициент теплоотдач α = 100 Вт/(м² ^. К)) с окружающей средой, которая имеет температуру Т _ж= 300 К. Нагреватель, который имеет температуру поверхности Т _н = 673 К, плотно прилегает к поверхности бруса (термическим сопротивлением воздушной прослойки между брусом и нагревателем можно пренебречь). Какое время должный работать нагреватель, чтобы температура бруса на противно-положной стороне стала равной Т, К. Исходные данные для решения задачи приведены в табл. 5.1.

Таблица 5.1.

5 10 4 9 3 8 2 7 1 6

l₁ q₂

l₂

q₃

q₁

q₄

α, Т_ж

№

λ,Вт/(м_*К)

a, м₂/с

T,K

l₁, м

l₂, м

2,5^.10^-5

0,10

0,20

2,0^.10^-5

0,12

0,22

3,0^.10^-5

0,08

0,24

2,2^.10^-5

0,10

0,18

2,8^.10^-5

0,12

0,20

4,0^.10^-5

0,14

0,26

3,5^.10^-5

0,10

0,24

2,7^.10^-5

0,12

0,18

2,1^.10^-5

0,14

0,20

6. ОПТИМИЗАЦИЯ ПРОЦЕССОВ ТЕПЛООБМЕНА

Основной задачей при создании любого теплового оборудования является определение оптимальных конструктивных параметров его узлов. Это выдвигает требование выполнения большого количества теплотехнических расчетов. Цель этих расчетов – определение оптимальних параметров оборудования. На первуй стадии целесообразно проведение анализа отдельных процессов и элементов теплоэнергетического оборудования. Ниже приведены примеры и задачи анализа отдельных узлов теплоэнергетического оборудования.

Пример 6.1. Изменение распределения температур между телом

ребра и окружающей средой по длине ребра требует введение понятия коэффициента эффективности ребра. Рассчитать эффективность стального ребра (коэффициент теплопроводност λ_р = 45 Вт/(м ^. К), толщина ребра δ_р = 0,001 м), если высота ребра h_р изменяется 0,01...0,1 м. Коэффициент теплоотдачи от поверхности ребра к окружающему воздуху α_р = 20 Вт/ (м^2. К).

Решение. Коэффициент эффективности ребра рассчитывается по формуле

где Bi = α_рδ_р/ λ_р - число Био.

Для решения задачи в пакете программ Mathcad преобразуем с учетом значений теплофизических свойств материала ребра уравнение расчета эффективности ребра к удобному для расчетов виду 1884^.(0,1^.n⁾^-0,2. Построим график этой зависимости принимая изменения диамтра ребра от 0,01 до 0,1м с шагом 0,01 м.

Рис. 6.1. Зависимость приведеного значения

эффективности ребра от его высоты.

Из рис. 6.1. видно, что с увеличением высоты ребра его эффективность падает.

Пример 6.2. Между двумя плоскими стенками существует прослойка жидкости толщиной δ = 0,015 м. Температура одной поверхности Т1 = 298 К, другой - Т2 = 328 К. Определить какую жидкость целесообразно залить между этими стенками, чтобы получить максимальное значение эквивалентной теплопроводности этой прослойки жидкости.

Решение. Числа подобия, которые характеризуют процесс теплообмена при естественной конвекции в прослойки жидкости:

Gr _δ = g δ³β^.(T ₁ – T ₂)/ν²; Ra = Gr_δ ^. Pr.

Коэффициент конвекции [3]:

ε = 0,4 ^. Ra ^0.2,

тогда значение эквивалентной теплопроводности λ_э = ε ^.λ.

Для решения задачи рассмотрим физические свойства следующих жидкостей для средней их температур: T = (T ₁+ T ₂)/2 = (298 + 328)/2= 313 K: вода λ= 0,635 Вт/(м ^.К); ν = 6,59^.10^-7м²/с; β=3,87^.10^-4 1/К; Pr = 4,31; хладон R22 – λ = 0,08 Вт/(м ^.К); ν = 1,96 ^,10^-7 м²/з; β = 39,95^.10^-4 1/К; Pr = 3,67; хладон R 113 – λ = 0,068 Вт/(м ^.К); ν = 3,59^.10^-7 м²/с; β=15,4^.10^-4 1/К; Pr=7,88; хладон R 11 – λ = 0,084 Вт/(м ^.К); ν = 2.6 ^.10^-7 м²/с; β = 16,5 ^,10^-4 1/К; Pr = 4,09.

Выполним расчеты в пакете программ Mathcad:

На основании выполненных расчетов можно сделать вывод, что как жидкость с высокой эффективной теплопроводностью целесообразно использовать воду.

Пример 6.3. Теплообменник для охлаждения воды представляет собой бак, внутри которого расположенный змеевик. Хладагент - водный раствор хлористого натрия. Диаметр трубок змеевика - d = 0,021 г. Средние температуры внутренней поверхности трубы T_t = 273 K и раствора Т _р = 270 К. Скорость движения раствора w = 1,2 м/с, концентрация раствора ξ = 11 %. Тепловой поток, переданный раствору от воды - Q = 10 квт. Определить изменение общей длины трубки змеевика при изменении его радиуса R = 0,2...0,6 м.

Решение. Физические свойства раствора хлористого натрия при температуре 270 К [9]: λ = 0,55 Вт/(м ^.К); ν = 2,1 ^.10^-6 м²/с; Pr = 15,2. Число Прантдля при температуре 273 К:Pr_с= 13,4.

Число Рейнольдса Re = wd / ν = 1,2 ^.0,021/2,1^.10 ^-6 = 1,2 ^.10 ⁴.

Среднее значение числа Нуссельта (табл.6.2. [2])

Nu=0,021^. Re^0,.8. Pr^0,43. (Pr/Pr_с)^0,25 = 0,021^. (1,2^.10⁴)^0,8. 5,2 ^0,43.(15,2/13,4) ^0,25= 128.

Коэффициент теплоотдачи без учета изгиба труб:

α = Nu ^. λ / d = 128 ^. 0,55 /0,021 = 3560, Вт/(м^2.К).

Коэффициент теплоотдачи с учетом изгиба труб:

α' = α ( 1 + 1.8 d/r), Вт/(м^2.К).

Тогда длина змеевика в зависимости от его радиусу имеет вид:

l = Q /(πdα'ΔT), м.

В результате расчетов имеем следующую зависимость длины змеевика от его радиуса для обозначенных условий:

Рис. 6.2. Зависимость длины змеевика от его радиуса.

Пример 6.4. В воде, температура которой Т ₁ = 293 К, происходит плавление льда. Лед имеет форму кубиков с стороной l = l м. Температура льда Т ₂= 273 K. Определить время, за которое кубики льда растают, если l = 0,05; 0,1; 0,15 и 0,20 м.

Решение. Физические свойства воды при температуре 293 К:

λ = 0,559 Вт/(м^.К); ν= 1^.10^-6м²/с;β = 1.82^.10^-4 1/К;Pr = 7,02.

Число Нуссельта определяется по следующей зависимости [9]:

Nu = Fo/K = 0,2 ^. (Gr_l^.Pr)^0,038,

Значение числа К = 4,0 [8]. Произведение чисел Grl ^.Pr определяется сле-дующим образом:

τ = 0,2^.[(gl ³β(T ₁ – T ₂)/ ν²)^. Pr ]⁰^,^038. K ^. l ²/ a.

Вычисления дают зависимость времени, за который кубик льда умень-шается, в зависимости от его первоначального размера (рис.9).

Рис.6.3. Изменение размера кубика льда в зависимости от его начального размера

Пример 6.5. Исследовать влияние количества экранов из алюминиевой фольги между стенками сосуда с жидким водородом с целью обеспечения максимального изоляционного эффекта. Степень черноты обоих поверхностей алюминиевой фольги ε₁= ε₂ = 0,05. Степень черноты стенок двухстенного сосуда ε_с1 = ε_с2 = 0,02.

Решение. Для указанных условий равенства степени черноты поверхнос-тей всех экранов приведенную ступней черноты можно определить по уравнению _n

ε_пр = 1/ [1/ε_с1 + 1/ε_с2– 1 + Σ(1/ ε_1i + 1/ ε_2і-1)],

ⁱ⁼¹

где n - количество экранов между стенками сосуда.

При подставке значения величин, получим ε_пр = 1/(9 + 39 n).

Решение имеет такой вид

Рис 6.3. Зависимость ε_пр от количества экранов n.

ЗАДАЧИ

Задача 6.1. Стенка бака испарителя обмывается водным раствором хло-ристого кальция, скорость движения раствора w = 0,6; 0,8 и 1,0 м/с. Высота стенки бака l ₁=0,6 м, а его длина l ₂ = 1,2 м. Концентрация раствора ξ =18,9 %. Температура стенки Т ₁ = 273 К, а температура раствора Т ₂ = 263 К. Раствор движется вдоль стенки бака в горизонтальном направлении.

Определить влияние скорости потока на средний коэффициент теплоотдачи α_ср от стенки бака к водному раствору хлористого кальция.

Задача 6.2. Как измениться средний коэффициент теплоотдачи

от стенки бака к водному раствору хлористого кальция α_ср, если раствор будет двигаться в вдоль стенки бака в вертикальном направлении. Вся остальные условия приведены в задаче 6.1.

Задача 6.3. Трубу, внешним диаметром d = 0,032, обтекает поток воды под углом γ = γ, градусов. Скорость потока воды w = 5 м/с. Температура потока воды Т ₁ = 303 К, температура стенки - Т ₂ = 275 К.

Определить влияние угла наклона трубы к направлению движения воды на плотность теплового потока от воды к трубе, если угол наклона γ изменяется от 0 до 45 градусов.

Задача 6.4. Исследовать влияние внутреннего диаметра трубы (диаметр трубы изменяется 0,006...0,020 м) на коэффициент теплоотдачи и температуры насыщения Т _н при кипении в ней хладону R 11. Удельная массовая затрата хладона G_m = 90 кг/ч. Температура насыщения - Т _н = 243; 253; 263; 273 и 283 К, температура стенки Т _ст = Т _н + 3 К. Уравнение для расчета коэффициента теплоотдачи:

α = 2,652.10^4. (Т _ст- Т _н)^1,5. G_m ^0,^5. F(p) ^2,5/ d ^1,5,

где G_m -массовая затрата хладону, кг/с; F(p) - значение функции приведено ниже:

Т _н, К 243 263 283 303

F(p) 0,0057 0,0082 0,0104 0,0136.

Задача 6.5. Выполнить аналогичные исследования для хладона R 12. Значение функции F(p) для хладона R 12 приведены ниже:

Т _н, К 243 263 283 303

F(p) 0,0146 0,0180 0,0212 0,0254.

Задача 6.6. Выполнить аналогичные исследования для хладона R2 2. Значение функции F(p) для хладона R2 2 приведены ниже:

Т _н, К 243 263 283 303

F(p) 0,0164 0,0202 0,0254 0,0301.

Задача 6.7. На внешней поверхности горизонтальной трубы осуществляется пленочная конденсация водного пара при давлении насыщения р = 4,242 х 10³ Па. Температура поверхности стенки трубы Т_с = 290 К. Определить влияние диаметра трубы на коэффициент теплоотдачи. Формулы для расчета теплообмена при конденсации пара представлены в табл. 8.1 [2].

Задача 6.8. Потолочная однорядная батарея состоит из гладких труб внешним диаметром d = 0,04 м. Размеры потолка 4 х4 м. Трубы покрытые инеем (ε_ин = 0,825). Температура инея Т _и= 263 К. Температура потолка Т_с = 275 К (ε_с= 0,91).

Оптимизовать шаг труб в потолочной батарее и определить общую длину труб, исходя из условия минимального лучистого потока от потолка к батарее, учитывая, что основной тепловой поток излучения поступает от потолка.

Задача 6.9. В печи с размерами 2 х 3,6 м для выпечки хлеба температура газов составляет Т _г = 523 К. В газах помещаются двуокись углерода (СО₂) и пары воды (Н₂О). Температура пода и хлеба, который выпекается, T = 463 К. Степень черноты этих тел - ε = 0,85.

Определить изменен

⇐ Предыдущая 12
Поделиться:

Воспользуйтесь поиском по сайту: