 |
1.2. Последовательный поиск. 1.3. Методы поиска посредством сравнения ключей. 1.3.1. Бинарный поиск. 1.3.2. Метод золотого сечения
|
|
|
|
1. 2. Последовательный поиск
Под последовательным поиском подразумевается исследование записей в том порядке, в котором они встречаются в наборе. Этот метод можно использовать для поиска в упорядоченной и неупоря-
доченной последовательности запи-сей. Он заключается в последова-тельном сопоставлении аргумента поиска А с ключом каждой записи. В неупорядоченной последователь- ности сопоставление ключей про- должается до тех пор, пока не будут просмотрены все N записей. Запись с искомым ключом выводится на печать.
Возможно ускорение работы последовательного поиска путем добавления в конец последовательности записей фиктивной записи X 
с ключом K , равным аргументу поиска А.
Структурограмма алгоритма последовательного поиска в этом случае будет выглядеть как на рис. 1.
Выигрыш в быстродействии здесь достигается за счет того, что проверка на окончание последовательности записей выполняется лишь один раз - при совпадении аргумента поиска с ключом записи.
Пример. Осуществить последовательный поиск аргумента 32
в массиве ключей: 37 25 32 29 20 *.
i = 1: 37 25 32 29 20 **.
i = 2: 37 25 32 29 20.
i = 3: 37 25 32 29 20.
Поиск окончен удачно, ключ 32 имеет порядковый номер, равный 3.
1. 3. Методы поиска посредством сравнения ключей
В последовательности, упорядоченной по возрастанию ключей записей, поиск можно прекратить сразу же, как только значение ключа текущей записи превысит значение аргумента поиска.
Известны следующие методы поиска посредством сравнения ключей в последовательности записей с упорядоченными ключами:
|
|
|
бинарный, однородный бинарный, золотого сечения, интерполяционный, Фибоначчиев, блочный и др., различающиеся лишь в выборе ключа K 
для его сравнения с аргументом поиска А. При этом всегда предполагается, что если А имеется в последовательности ключей, то K 
< = A < = K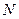 
.
1. 3. 1. Бинарный поиск
Бинарный (двоичный, дихотомический, половинного деления) поиск относится к наиболее эффективным методам поиска в упорядоченной последовательности записей. Идея этого метода состоит в том, чтобы искать ключ А в интервале, крайними точками которого являются два указателя - Q и P, соответствующие нижней и верхней границам поиска. Вначале А сравнивается со средним ключом в последовательности. Результат сравнения позволит определить, в какой половине последовательности продолжить поиск, применив к ней ту же процедуру, и т. д. После определенного числа сравнений либо ключ будет найден, либо будет установлено его отсутствие. Структурограмма алгоритм бинарного поиска представлена на рис. 2.
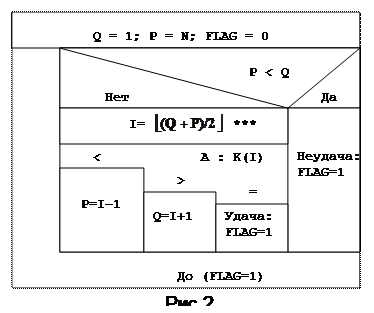Пример. Осуществить бинарный поиск аргумента 51 в массиве ключей: 20 25 29 32 37 38 39 51 53 57 61 99.
Q=1, P=12, i=6, Ki=38: [20 25 29 32 37 38 39 51 53 57 61 99].
Q=7, P=12, i=9, Ki=53: 20 25 29 32 37 38[39 51 53 57 61 99].
Q=7, P=8, i=7, Ki=39: 20 25 29 32 37 38[39 51]53 57 61 99.
Q=8, P=8, i=8, Ki=51: 20 25 29 32 37 38 39[51]53 57 61 99.
Поиск заканчивается удачно, ключ 51 имеет элемент с номером 8.
*** Операция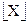 
означает взятие от X наибольшего целого, меньше-
го или равного X.
1. 3. 2. Метод золотого сечения
При поиске методом золотого сечения аргумент поиска А
сравнивается с ключом K , где i является золотым сечением
интервала поиска. Сущность золотого сечения заключается в том, что если на плоскости имеется отрезок длиной а, то золотое сечение делит его на два отрезка соответственно длиной в и с так, что а/в =
= в/с.
Для уменьшения временных затрат при реализации вычисления золотого сечения используют константу, на которую надо разделить интервал а, чтобы найти его золотое сечение. Эта константа равна а/в = в/с = 1. 619031... .
|
|
|
Алгоритм поиска методом золотого сечения аналогичен алгоритму бинарного поиска (рис. 2). Отличие состоит только в шаге вычисления номера I сравниваемого элемента, который в данном случае принимает вид:
I=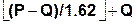 
.
Пример. Осуществить поиск методом золотого сечения аргумента 51 в массиве ключей: 20 25 29 32 37 38 39 51 53 57 61 99.
Q=1, P=12, i=7, Ki=39: [20 25 29 32 37 38 39 51 53 57 61 99].
Q=8, P=12, i=10, Ki=57: 20 25 29 32 37 38 39 [51 53 57 61 99].
Q=8, P=9, i=8, Ki=51: 20 25 29 32 37 38 39[51 53]57 61 99.
Поиск заканчивается удачно, ключ 51 имеет элемент с номером 8.
|
|
|
