 |
1.3.3. Интерполяционный поиск. 1.3.4. Однородный бинарный поиск. Примечания. 1.3.5. Фибоначчиев поиск. 1.3.6. Блочный поиск
|
|
|
|
1. 3. 3. Интерполяционный поиск
Главное отличие интерполяционного поиска от предыдущих методов заключается в том, что выбор очередного ключа K 
для сравнения с аргументом А зависит не только от Q и P, но и от значений ключей K 
и K 
в нижней и верхней границах интервала поиска. Если аргумент поиска А на очередном шаге лежит между K и K , то ключ K выбирается на расстоянии (P-Q)(A-K )/(K -K ) от Q в предположении, что ключи являются числами, возрастающими приблизительно как арифметическая прогрессия.
Алгоритм интерполяционного поиска также аналогичен алгоритму бинарного поиска (рис. 2). Отличие состоит только в шаге вычисления номера i сравниваемого элемента, который в данном случае имеет вид: I=(P-Q)(A-K )/(K -K ) + Q.
Пример. Осуществить интерполяционный поиск аргумента 51 в
массиве ключей: 20 25 29 32 37 38 39 51 53 57 61 99.
Q=1, K =20, P=12, K =99, i=5, Ki=37: [20 25 29 32 37 38 39 51 53 57 61
99].
Q=6, K =38, P=12, K =99, i=8, Ki=51: 20 25 29 32 37[38 39 51 53 57 61 99].
Поиск закончен удачно, ключ 51 имеет элемент с номером 8.
1. 3. 4. Однородный бинарный поиск
При однородном бинарном поиске аргумент поиска А сравнивается с ключом K , находящимся в середине интервала поиска. Отличие этого метода от бинарного поиска заключается в том, что вместо трех указателей Q, i и P используются только два: текущее положение i и величина его изменения H. После каждого сравнения A и K , не давшего равенства, устанавливается i =i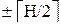 
и H=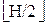 
. Поиск заканчивается неудачно, если приращение становится равным 0.
Структурограмма алгоритма поиска приведена на рис. 3.
Примечания
1. При нечетном N необходимо ввести фиктивную запись X 
с ключом K < A.
2. 
- операция означает взятие от числа наименьшего целого, большего или равного Х.
|
|
|
Пример. Осуществить однородный бинарный поиск аргумента 30 в массиве ключей: 20 25 29 32 37 38 39 51 57 61 99.
i=6, H=6: [20 25 29 32 37 38 39 51 57 61 99].
i=3, H=3: [20 25 29 32 37]38 39 51 57 61 99.
i=5, H=1: 20 25 29[32 37]38 39 51 57 61 99.
i=4, H=0: 20 25 29[32]37 38 39 51 57 61 99.
Так как H = 0, а K # A, поиск заканчивается неудачно.
1. 3. 5. Фибоначчиев поиск
При реализации этого метода для нахождения интервала поиска
используются числа Фибоначчи. Числа Фибоначчи получаются по рекуррентной формуле
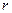F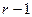 
= F 
+ F 
, где r = 3, 4, 5,..., F 
= 0, F 
= 1.
В методе Фибоначчи, так же как и в однородном бинарном поиске, используются два указателя: i - текущее положение и величина H изменения, но они выбираются в соответствии с числами Фибоначчи. Значение i выбирается равным числу Фибоначчи F 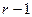, а Н - равным F 
.
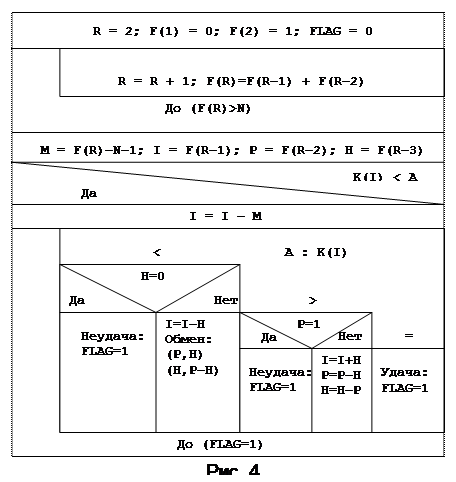
Алгоритм Фибоначчиева поиска состоит из предварительного этапа и 4 шагов. Первоначально определяется такое число M> =0, что N + M + 1 = F 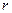, где F 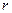> N есть ближайшее к N число Фибоначчи. Устанавливают i = F 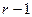, P = F , H = F . Если первый проверяемый ключ K < A, то устанавливают i = i - M.
Структурограмма алгоритма поиска приведена на рис. 4.
Пример. Осуществить Фибоначчиев поиск аргумента 57 в массиве ключей: 20 25 29 32 37 38 39 51 53 57. Так как N=10, то ближайшим большим N числом Фибоначчи является число F 
=13, так что M = 2, i = F 
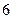= 8, P = F 
= 5, H = F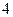 
= 3: [20 25 29 32 37 38 39 51 53 57]. Так как A > K 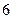(57> 51), то I = I – M = 6, I = 9, P = 2, H = 1:
20 25 29 32 37 38 39 51[53 57]. I = 10, P = 1, H = 0: 20 25 29 32 37 38 39 51 53[57]. Искомый ключ имеет элемент с номером i = 10.
1. 3. 6. Блочный поиск
Идея данного метода заключается в том, чтобы делить интервал поиска не на два подынтервала, а на несколько. Эти подынтервалы называются блоками.
Вначале ищется блок, 
в котором может находиться аргумент поиска, путем сравнения его с последними ключами записей в блоках. Если A< K , то аргумент поиска А должен находить- ся (если он вообще есть) в данном блоке. В этом случае нижняя граница интервала поиска устанав- ливается на 1-ю запись этого блока, а верхняя граница - на последнюю запись блока. Затем снова разбивается новый интервал поиска на блоки и т. д. Если при очередном сравнении A > K , то в данном блоке ключа А нет. Затем сравнивается последний ключ следующего блока и т. д. Наиболее рационально делить интервал поиска, состоящий из N записей, на блоки из 
записей.
|
|
|
Структурограмма алгоритма блочного поиска представлена на рис. 5.
Пример. Осуществить блочный поиск аргумента 30 в массиве ключей: 20 25 29 32 37 38 39 51 53 57 61 99.
Q=1, P=12, H=3, i=3: [20 25 29 32 37 38 39 51 53 57 61 99].
i=6: 20 25 29 [32 37 38 39 51 53 57 61 99].
P=5, Q=4, H=1, i=4: 20 25 29 [32 37]38 39 51 53 57 61 99.
P=3, Q=4, H=1, i=4: 20 25 29][32 37 38 39 51 53 57 61 99.
Поиск заканчивается неудачно.
|
|
|
