 |
Модель местных упругих деформаций и упругого полупространства
|
|
|
|
При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи. Наибольшее распространение в инженерной практике получили следующие модели основания:
- модель упругих деформаций;
- модель упругого полупространства.
Модель местных упругих деформаций.
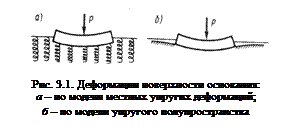
Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке, а осадки поверхности основания за пределами габаритов фундамента отсутствуют (рис. 3.1.а.):
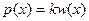, (3.2)
где 
– коэффициент пропорциональности¸ часто называемый коэффициентом постели, Па/м.
Модель упругого полупространства.
В этом случае поверхность грунта оседает как в пределах площади загрузки, так и за её пределами, причём кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании (рис. 3.1.б.):
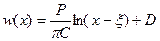, (3.3)
где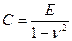 
- коэффициент жесткости основания, 
– координата точки поверхности, в которой определяется осадка;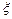 
- координата точки приложения силы 
; 
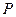– постоянная интегрирования.
Влияние жесткости фундаментов на распределение контактных напряжений.
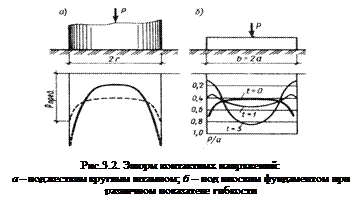Теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям. Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуется более пологой кривой и у края фундамента достигает значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 3.2.а.)
Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 3.2.б. приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.
|
|
|
Распределение напряжений в грунтовых основаниях от собственного веса грунта.
Вертикальные напряжения от собственного веса грунта на глубине z от поверхности определяются формулой:
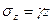, (3.4)
а эпюра природных напряжений будет иметь вид треугольника (рис. 3.3.а)
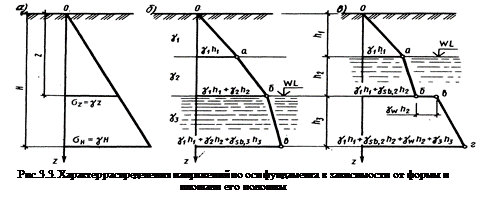При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра будет уже ограничиваться ломаной линией Оабв, где наклон каждого отрезка в пределах мощности слоя 
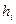определяется значением удельного веса грунта этого слоя 
(рис. 3.3.б).
Неоднородность напластования может вызываться не только наличием слоев с разными характеристиками, но и наличием в пределах толщи грунта уровня подземных вод (WL на рис. 3.3.в). В этом случае следует учесть уменьшение удельного веса грунта за счет взвешивающего действия воды на минеральные частицы:
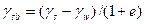, (3.5)
где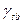 
- удельный вес грунта во взвешенном состоянии; 
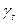- удельный вес частиц грунта; 
- удельный вес воды, принимаемый равным 10 кН/м3;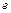 
– коэффициент пористости грунта.
Лекция 4.
Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности.
Распределение напряжений в основании зависит от формы фундамента в плане. В строительстве наибольшее распространение получили ленточные, прямоугольные и круглые фундаменты. Таким образом, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.
Напряжения в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения.
|
|
|
