 |
Задача о действии вертикальной сосредоточенной силы.
|
|
|
|
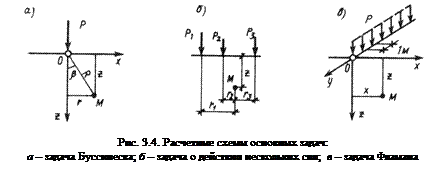Решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства полученное в 1885 г. Ж. Буссинеском, позволяет определить все компоненты напряжений и деформаций в любой точке полупространства 
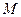от действия силы 
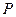(рис. 3.4.а).
Вертикальные напряжения определяются по формуле:
, где 
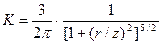. (3.6)
Используя принцип суперпозиции можно определить значение вертикального сжимающего напряжения в точке 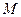при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 3.4.б):
(3.7)
В 1892 г. Фламан получил решение для вертикальной сосредоточенной силы 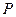в условиях плоской задачи (рис. 3.4.в):
; 
; 
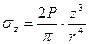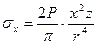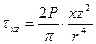, где 
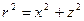(3.8)
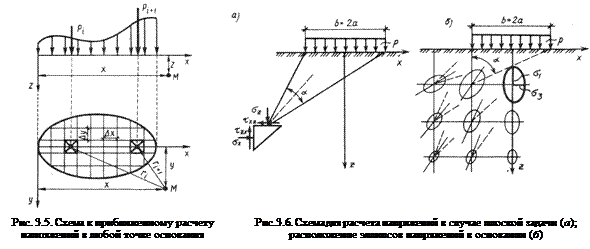
Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (3.6) в пределах этого контура, определить значения напряжений в любой точке основания для случая осесимметричной и пространственной нагрузки (рис. 3.5.), а интегрируя выражение (3.8) – для случая плоской нагрузки.
Плоская задача. Действие равномерно распределенной нагрузки.
Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью 
показана на рис. 3.6.а.
Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:
; 
; 
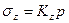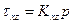, (3.9)
где 
, 
, 
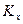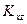- коэффициенты влияния, зависящие от безразмерных параметров 
и 
; 
и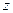 
– координатные точки, в которой определяются напряжения; 
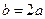– ширина полосы загружения.
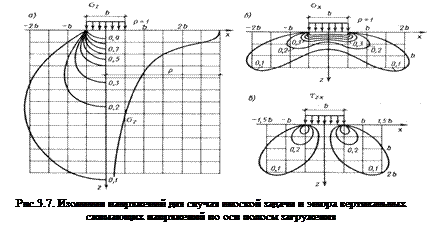На рис. 3.7. а-в показано в виде изолиний распределение нарпряжени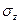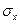и 
, 
и 
в массиве грунте для случая плоской задачи.
|
|
|
В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:
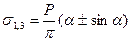, (3.10)
где 
- угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис.3.6.б).
Пространственная задача. Действие равномерно распределенной нагрузки.
В 1935 г. А. Лявом были получены значения вертикальных сжимающих напряжений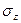 
в любой точке основания от действия нагрузки интенсивностью , равномерно распределенной по площади прямоугольника размером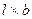 
.
Практический интерес представляют компоненты напряжений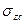 
, относящиеся к вертикали, проведенной через угловую точку 
этого прямоугольника, и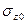 
, действующие по вертикали, проходящей через его центр (рис. 3.8.).
Используя коэффициенты влияния можно записать:
; 
, (3.11)
где - 
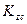и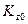 
- соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.
Между значениям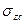и и 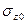имеется определенное соотношение.
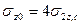. (3.12)
Тогда оказывается удобным выразить формулы (3.11) через общий коэффициент влияния и записать их в виде:
; 
. (3.13)
Коэффициент зависит от безразмерных параметров 
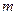и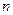 
: 
, 
(при определении углового напряжения ), 
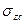(при определении напряжения под центром прямоугольника ).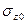
Метод угловых точек.
Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения (рис.3.9.).
Пусть вертикаль проходит через точку 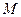, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения 
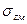как сумму угловых напряжений I и II прямоугольников, т.е.
|
|
|
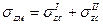. (3.13)
Если точка 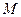лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда:
. (3.14)
Наконец, если точка 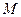лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой.
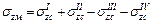. (3.15)
3.3.5. Влияние формы и площади фундамента в плане.
На рис. 3.10. построены эпюры нормальных напряжений 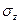по вертикальной оси, проходящей через центр квадратного фундамента при 
(кривая 1), ленточного фундамента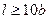 
(кривая 2), и тоже, шириной 
(кривая 3).
 |
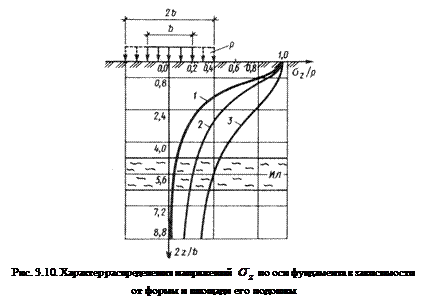В случае пространственной задачи (кривая 1) напряжения с глубиной затухают значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к ещё более медленному затуханию напряжений с глубиной.
Лекция 5
|
|
|
