 |
Вращательные движения твердого тела.
|
|
|
|
Вращательным движением называется такое движение твердого тела, при котором остаются неподвижными все (.), лежащие на некоторой прямой, называемой осью вращения.
φ В
 | |||
| |||
| |||
 | |||
 | |||
| |||
 | |||
1
А
Закрепляем 2 (.) тела А и В, прямая АВ будет осью вращения. Все остальные (.) тела движутся в плоскостях ┴ оси вращения, описывая окружности, центры которых лежат на этой оси.
Для определения положения вращения тела проводим через ось вращения z 2 полуплоскости: неподвижную полуплоскость 1 и подвижную 2, связанную с твердым телом и вращающуюся вместе с ним.
Двугранный угол φ между 2 мя полуплоскостями, отсчитываемый от неподвижной полуплоскости, называется угол поворота тела.
φ «+» если, смотря навстречу оси вращения, могли увидеть его отложенным против движения часовой стрелки и φ «-», если по ходу часовой стрелки. Измеряется φ в радианах.
(радианом называется центральный угол, длина дуги, которого равна радиусу. Числовое значение угла в радианах = отношению дуги к радиусу, то есть отвлеченное число).
3600 = 2 π рад. Один радиан составляет
Если тело совершило N оборотов, то угол поворота φ = 2πN.
Чтобы знать положение тела в любой момент, надо знать зависимость угла φ от времени.
φ = f(t) (2.4)
Уравнение (2.4) называется уравнением вращательного движения тела.
Основными кинематическими характеристиками вращающегося тела является его угловая скорость ω и угловое ускорение Е.
Если за промежуток времени ∆t =t1 –t тело совершило поворот на угол ∆φ = φ1 – φ, то средняя угловая скорость тела за этот промежуток времени будет численно равна.
|
|
|
ωср = 
(2.5)
Угловой скоростью тела в данный момент времени t называется к которой стремится значение ωср, когда ∆t → 0
ω = 
= φ (2.6)
Т.о угловая скорость равна в данный момент времени первой производной от угла поворота по времени.
Знак ω определяется направлением вращения тела.
ω = > 0 – Вращение в положительное направление.
ω = < 0 – Вращательное в отрицательном направлении.
Размерностью угловой скорости радиан/секунду или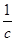 
=с-1 так как радиан величина безразмерная.
Угловую скорость тела можно изобразить в виде вектора ω, численная величина которого равна и который направлен вдоль оси вращения в ту сторону, откуда вращения видно происходящим против часовой стрелки.
|
В
 |
ω
Е
А
Угловое ускорение характеризует изменение угловой скорости тела с течением времени.
Если за промежуток времени ∆t = t1 – t угловая скорость тела изменится на величину ∆ω = ω1 – ω, то среднее угловое ускорение за этот промежуток времени
Еср = 
(2.7)
Угловым ускорением тела в данный момент времени t называется величина, к которой стремится значение Еср, когда ∆t → 0
Е = 
(2.8)
Итак, угловое ускорение тела в данный момент времени численно равной первой производной от угловой скорости по времени или второй производной от угла поворота по времени.
Размерность Е [рад/с2][с-2]
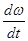>0, тело вращения ускорено.
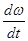<0, тело вращения замедленно.
Угловое ускорение можно изобразить в виде вектора Е, направленного по оси вращения.
Равномерное и равнопеременное вращение.
Если ω =const, то вращение равномерное.
Найдем закон равномерного вращения. Из формулы (2.6)
Имеем dφ =ωdt отсюда, считая, что в начальный момент при t=0 φ=0 и беря интегралы.
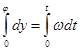, получим φ=ωt (2.9)
Отсюда найдем ω= φ/t (2.10)
В технике скорость равномерного вращения определяют числом оборотов в мин, (n об/мин – частота вращения).
|
|
|
1 оборот – 2π
n - оборот – 2πn это за 1 мин.
ω =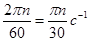 
Если Е- const, то вращение равнопеременное.
Найдем закон равнопеременного вращения.
(Начальный момент t=0 φ=0 ω=ω0 нач. угловая скорость).
Из формулы (2.8) имеем dω=Е dt, интегрируя
(2.11) ω=ω0+Еt или
= ω0+Еt
dφ = (ω0+Et)dt
Вторично интегрируя, найдем значение равнопеременного вращения.
φ =ω0t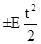 
(2.12)
|
|
|
