 |
Скорость и ускорение точек вращающегося тела.
|
|
|
|
Изобразим траекторию произвольной точки М твердого тела совершающего вращательное движение (окружность радиуса R).
a V
C β ae
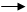φ α aω M
O N
ОС –радиус лежащий в неподвижной полуплоскости 1.
NC – радиус лежащий в подвижной полуплоскости 2.
ﮮ OCN – φ угол поворота ﮮα = const.
S =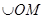 
=R (φ+α) - так можно определить положение (.) М
υ= 
υ=R*ω (2.13)
Модуль вращательной скорости (.) твердого тела производной расстоянию от точки до оси вращения на угловую скорость тела.
Направлена вращательная скорость (.) по касательной.
Так как ω для всех (.) одинакова из формулы (2.13) следует, что линейная скорость (.) вращающегося тела пропорциональны их расстояниям от оси вращения.
 |
C ω
Для нахождение ускорения (.) М воспользуемся формулами.
ar = 
an=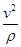 
В нашем случае.
(2.14) ar=R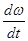 
= R*E= ae Вращательное ускорение.
(2.15) an= 
=ω2R= aω Центростремительное ускорение.
Модуль полного ускорения.
(2.16) a =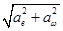 
= 
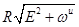
Определяем тангенс угла наклона ω с радиусом СМ.
(2.17) tg β=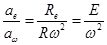 
(не зависит от положения (.))
(не зависит от положения (.)).
Плоское движение твердого тела.
Плоским или плоскопараллельным движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
M1
Q1 V1 W1
 | ||
 |
M
Q2 V W
M2
Q3 V2 W2
Плоская фигура образованная сечением тела этой неподвижной плоскости Q, все время движения остается в этой плоскости (рис.)
Плоскость Q1//Q2//Q М1→ пл. Q1 M2→Q2 отрезком М1М2 остается // своему первоначальному положению.
(.) перпендикуляра, как и (.) твердого тела, движущегося поступательно имеют тождественную траекторию и в каждый данный момент геометрически равные скорости и ускорения.
|
|
|
v1 =v2 = v и w1 =w2 = w
Движение каждой (.) плоской фигуры в неподвижной плоскости определяет собой движение всех (.) твердого тела. Расположенных на ┴ к плоскости Q, восстановленном в этой точке. Это позволяет свести изучение плоскости движения твердого тела к изучению движения плоской фигуры в ее плоскости.
А
А В
В
Положение плоской фигуры на плоскости определяется положением 2 х ее (.) (или прямой).
Разложение движения плоской фигуры на поступательное движение вместе с полюсом и вращение вокруг полюса.
Уравнения движения плоской фигуры.
 |
B B1 β`
φ1 φ2
A A1
1 2
Совокупность двух движений поступательного и поворота.
Поступательное движение различно в различных вариантах, а поворот одинаков.
φ1 =φ2
Из этого следует, что всякое непоступательное движение плоской фигуры в ее плоскости можно рассматривать как совокупность 2 х перемещений: поступательного перемещения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг полюса.
Поступательное движение зависит от выбора полюса, а величина и направление поворота от выбора полюса не зависит.
y1
y y1 M x1
α
О φ x1
y0 x0
x
О
Уравнение плоского движения твердого тела.
W=φ+α x0=f1(t)
α –const y0=f2(t)
φ=f3(t)
В1
O1 φ1 а1
φ2
О2 а2
Покажем, что вид уравнения φ = f3 (t) не зависит от выбора полюса.
О1А1//О2А2 во все время движения (движутся поступательно вместе с полюсом)
О1В1//О2В2
φ1 = φ2 = φ = f3 (t)
Основными кинематическими характеристиками плоского движения являются скорость и ускорение поступательного движения, а так же угловая скорость и угловое ускорение вращательного движения вокруг полюса.
α-const
φ=φ1+α
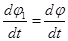
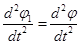
ω1=ω E1=E
y
В1 Д
|
|
|
С φ φ1 B
φ
А
x
O1
В качестве полюса можно выбрать любую (.) тела.
α = const
φ = φ1 + α
ω1 = ω Е1 = Е
Характеристики вращательного движения остаются неизменными. Характеристики поступательного движения изменятся υе ≠ υа
Векторы ω и е направлены по оси, проходящей через полюс, перпендикулярно плоскости фигуры.
ω
Е
O О
Е
Е ω
|
|
|
