Проектирование КИХ-фильтров в MATLABе

Заключительной проблемой проектирования линейного цифрового фильтра является вычисление векторов коэффициентов числителя 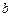и знаменателя его дискретной передаточной функции .

Представленная дискретная передаточная функция описывает в сжатой форме такое конечно-разностное уравнение фильтра:

КИХ-фильтр описывается только одним вектором 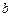. Знаменатель этой дискретной передаточной функции тождественно равен 1.

Группа функций fir1 предназначена для расчета коэффициентов 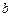цифрового КИХ-фильтра с линейной фазой методом взвешивания с использованием окна. Общий вид обращения к этой процедуре

b = fir1 (n, Wn, 'ftype', window).

Процедура вычисляет вектор n+1 коэффициентов 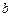КИХ-фильтра с нормализованной частотой среза Wn.

Все функции проектирования фильтров работают с нормализованными частотами, так что они не требуют системную частоту дискретизации как дополнительный входной аргумент. Используется соглашение, что единичная частота - частота Найквиста, определенная как половина частоты дискретизации. Нормализованная частота, поэтому, находится всегда в интервале . Для системы с частотой дискретизации 1000 Гц, 300 гц - 300/500 = 0.6. Чтобы преобразовывать нормализованную частоту назад в Герц надо умножить наполовину частоту дискретизации.

Параметр 'ftype' задает желаемый тип фильтра (ФНЧ, ФВЧ, полосовой или режекторный). Он может отсутствовать (и тогда по умолчанию рассчитываются параметры ФНЧ с частотой среза Wn, если параметр Wn задан в виде вектора из двух элементов рассчитывается полосовой фильтр с полосой пропускания от до ) или принимать одно из четырёх значений. В первом случае синтезируется ФВЧ с частотой среза Wn. Во втором — режекторный фильтр (прим этом Wn должен быть вектором из двух элементов, значения которых определяют границы полосы задерживания по отношению к частоте Найквиста). В третьем случае рассчитываются параметры многополосного фильтра, первая полоса которого является полосой пропускания, а в четвертом — тоже многополосный фильтр, первая полоса которого является полосой задерживания.

При расчете режекторных фильтров и ФВЧ порядок фильтра следует назначать четным числом.

Параметр window позволяет устанавливать тип окна. Если этот параметр не указан, то, по умолчанию, будет использовано окно Хемминга.

Окно используется, когда присутствует явление Гиббса. Как следствие явления Гиббса, частотная характеристика фильтров может содержать отклонения от номинала (идеальной характеристики) и скачки на краях полосы. Пока порядок фильтра остается конечным, эти беспорядки не могут быть устранены. При использовании функции окна эти скачки можно ограничить за счет крутизны фильтра

Для того чтобы вычислять окна различного типа используются следующие функции программы MATLAB:

- boxcar(n) создает вектор-столбец из n элементов прямоугольного окна. Это окно имеет одинаковое величину (единицу) для всех значений , в которых ответ импульса должен быть сохранен, и величина нуля для всех величин , в которых ответ импульса должен быть устранен:

, .

- triang (n) создает вектор-столбец, состоящий из n элементов треугольного окна. Дискретная функция окна

, .

- hamming (n) создает вектор-столбец из n элементов окна Хэмминга. Дискретная функция окна

, .

- blackman (n) создает вектор-столбец из n элементов окна Блэкмана. Дискретная функция окна

, .

Пример 1. Создайте цифровой ФНЧ 10 порядка с нормализованной частотой среза , с использование окна Хэмминга.

[b,а] = fir1 (10, 0.6).

MATLAB возвращает следующий

b =

0.0000 0.0127-0.0638 0.2760 0.5997

0.2760-0.0248 0.0127 0.0000

a = 1.