 |
Равновесие системы сходящихся сил.
|
|
|
|
1. Геом условие равновесия: Т.к. главный вектор 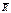 системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил,то
системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил,то 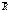 может обратиться в 0 только тогда,когда многоугольник замкнется, т.е. когда конец вектора последней силы совпадет с началом вектора первой силы. Исходя из этого для равновесия системы сходящихся сил необходимо и достаточно чтобы силовой многоугольник, построенный из этих сил был замкнутый.
может обратиться в 0 только тогда,когда многоугольник замкнется, т.е. когда конец вектора последней силы совпадет с началом вектора первой силы. Исходя из этого для равновесия системы сходящихся сил необходимо и достаточно чтобы силовой многоугольник, построенный из этих сил был замкнутый.
2. Аналитическое условие равновесия: Вектор  можно рассчитать аналитически
можно рассчитать аналитически 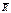 =
= 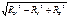 . Равнодействующая – сумма равнодействующих в каждой из пл-тей.
. Равнодействующая – сумма равнодействующих в каждой из пл-тей.  =0, когда RX=0, RY=0,RZ=0. ∑FX=0, ∑FY=0, ∑FZ=0. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей были равны 0.
=0, когда RX=0, RY=0,RZ=0. ∑FX=0, ∑FY=0, ∑FZ=0. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей были равны 0.
8 Момент силы. Пара сил
9. Момент силы относительно точки.
Точку, относительно которой берется момент – наз-ют центром момента, а момент силы, относительно этой точки – моментом относительно центра. Момент всегда характеризует вращательный эффект силы m0(F)=F•h
Моментом силы F, относительно центра т.О, наз-ся вектор m0(F), приложенный в центре т.О, модуль которого равен произведению силы F на ее плечо и направлен перпендикулярно плоскости, проходящей ч/з центр О. #
Св-ва момента силы:
1. Момент силы, относительно цента не изменяется при переносе т. приложения силы вдоль линии ее действия.
2. Момент силы относительно центра равен 0,или когда сила =0,или когда линия действия силы проходит ч/з т.О.(плечо =0)
10. Момент силы относительно оси.
Моментом силы, относительно оси, наз-ся взятое со знаком +или- произведение модуля проекции F1 силы F на пл-ть, перпендикулярную к оси, на плечо d1, относительно т.О – пересечения оси и пл-ти. M=F1 •d1. Если сила и ось лежат в одной пл-ти, то момент силы относительно этой оси=0. #
|
|
|
11. Пара сил. Момент пары сил.
Пара сил – система 2х сил, равных по модулю, параллельных и направленных в противоположные стороны. F= -F’. #
Момент пары сил – вектор T(M), модуль к-го равен произведению модуля одной из сил на ее плечо и к-й направлен перпендикулярно пл-ти действия пары сил в ту сторону, откуда пара сил видна стремящейся повернуть тело против хода часовой стрелки. Момент пары сил равен сумме моментов относительно любого центра т.О сил, образующих пару сил. m=m0(F)+m0(F’) #
Проведем из т.О радиус векторы rА=ОА и rВ=ОВ.
m0(F’)= –rB •F’, m0(F)= rА •F.
m=m0(F)+m0(F’)= rА •F– rB •F’=F(rА – rB)=AB•F (*)
Из (*) следует, что момент пары сил равен моменту 1 из сил, относительно т приложения другой силы. 2 пары сил имеющие одинаковые моменты – эквивалентные, т.е. оказывают на тело одинаковое механическое действие.
12. Теорема об эквивалентных парах.
Две пары сил, лежащие на одной пл-ти и имеющие равные алгебраические величины моментов – эквивалентны.
Док-во: # Рассм пару сил F и F’. Проведем в пл-ти действия этой пары,через произвольные т.D и т.E две параллельные прямые до пересечения их с линиями действия сил f и F’, и приложим силы P и –P’. Разложим каждую из сил F и F’ по направлениям (АВ) и (ЕВ) и по направлениям (АВ) и (AD) на две составляющие Q и P. P= –P’, Q= –Q’.
Q и –Q’ – лежит на 1й линии действия – воздействие =0.Остается P и P’. В результате пара сил F и F’ будет заменена парой сил p и P’ с другим плечом и другими силами, к-е можно приложить в т.d и т.E, на их линии действия, т.е. F и F’ можно заменить на P и P’.
13. Теорема о сложении пар сил
# Пары сил, лежащие в одной пл-ти, можно складывать. В рез-те сложения получается лежащая в этой же пл-ти пара сил с моментом, равным алгебраической сумме моментов слагаемых пар. Рассм две пары с моментами m1 и m2, лежащие в пл-тях I и II. Возьмем на линии пересечения пл-тей отрезок AB=В и изобразим пару с моментом m1 силами F1’ F1, а пару с моментом m2 силами F2’ и F2. Сложив силы, приложенные в т.А и т.В убеждаемся,что пары F1 и F1’ и F2 и F2’ – эквивалентны одной паре R и R’.
|
|
|
Так как R=F1+F2, то M(R)=AB•R=F1•AB+F2•AB. →M=m1+m2. Ч.т.д.
14. Приведение системы к центру
1.5.. Теорема о параллельном переносе силы.
Силу, приложенную к АТТ можно не изменяя оказываемого ей действия переносить из данной точки в любую другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы, относительно точки, куда переносится сила.
Пусть дана сила F, приложенная к АТТ в т.А и произвольная т.О, которую назовем центром приведения. # Проведем из т.О в т.А радиус-вектор r, тогда M0(F)=F•r. Приложим в т.О две уравновешивающие силы. F1’ и F” равные и параллельные силе f. M=F•d, M=M0(F). Т.к. векторы М и М0 равны по модулю и совпадают по направлению, то они геометрически равны. M=M0(F)=F•r. Метод Пуансо. Силу F не изменяя ее действия на твердое тело можно перенести из т. ее приложения в любой центр приведения, приложив при этом к телу пару сил с моментом М геометрически равным моменту этой силы, относительно центра приведения.
16. Приведение системы сил к заданному центру.
# Пусть на твердое тело действует произвольная система сил – f1,F2,…Fn, выберем т.О за центр приведения и пользуясь методом Пуансо перенесем все силы в т.О. F1=F1’, F2=F2’, Fn=Fn’. тогда на тело будут действовать: F1=F1’, F2=F2’, Fn=Fn’ приложенные в т.О и система пар сил m1=m2(F1), m2=m0(F2), mn=m0(Fn).
Сходящаяся система сил, приложенная в т О заменяется равнодействующей, равной сумме всех сил. R =∑F, R – главный вектор системы сил.
Чтобы сложить все полученные пары сил, надо сложить векторы моментов этих сил. M0=∑m0(F). М0= геометрической сумме моментов всех сил, относительно т О, наз-ся главным моментом системы сил, относительно этой т.(центра) #
17. Теорема о приведении системы сил.
Любая система сил, действующая на АТТ, при приведении к произвольному центру О, заменяется одной силой R, равной гл вектору сис-мы сил и приложенной в центре приведения т О и одной парой сил с моментом М0, равным гл моменту сис-мы сил, относительно центра О.
|
|
|
Следствие: 2 сис-мы сил, имеющие одинаковые главные векторы и главные моменты, относительно одного и того же центра – эквивалентные.
18. Условия равновесия системы сил.
Для равновесия любой системы тел необходимо и достаточно, чтобы гл. вектор этой системы и ее главный момент относительно любого центра были равны 0.
Эти условия являются необходимыми, т.к. если какое-нибудь из них не выполняется, то система действующих на тело сил, приводится к равнодействующей (R≠0) или к паре сил (М0≠0) и следовательно не является уравновешанной.
Одновременно условия являются и достаточными, потому что при R=0 система может приводиться только к паре сил с моментом М0, а т.к. М0=0, то имеет место равновесие.
19. Теорема Вариньона о моменте равнодействующей.
Если данная сис-ма сил имеет равнодействующую, то момент равнодействующей, относительно любого центра т.О равен сумме моментов сил, относительно того же центра.
Док-во: Пусть сис-ма сил F1, F2…Fn приводится к равнодействующей R, линия действия к-й проходит ч/з некоторую т.С. # Приложим в этой т. силу R’= -R, тогда сис-ма сил F1, F2…Fn, R’ будет находиться в равновесии и для нее должно выполняться условие М0=0, т.е. согласно формуле M0=∑m0(FK) для данных сил (включая силу R’), должно быть ∑m0(FK)+m0(R’)=0, но т.к. R’= -R и обе силы направлены вдоль одной прямой, то m0(R’)= -m0(R). Подставляя это значение m0(R’) в предыдущее равенство получим m0(R)= ∑m0(FK) Ч.т.д. (теорема для нахождения моментов сил).
20. Плоская система сил.
21. Алгебраический момент силы.
# Алгебраический момент силы F,относительно центра т.О, равен с соответствующим знаком взятому модулю силы на ее плечо. m0(F)=  Fh
Fh
22. Алгебраический момент пары сил.
Алгебраический момент пары сил = взятому с соответствующим знаком произведению модуля одной из сил на плечо силы.
23. Приведение плоской системы к простейшему виду.
Для плоской сис-мы тел: RX= ∑m0(FKX); RY=∑m0(FKY); M0= ∑m0(F) Плоская сис-ма сил, не находящаяся в равновесии приводится к простейшему виду: 1) Если для данной системы сил R=0, M0≠0, то она приводится к 1й паре сил с моментом m0. 2) Если для данной системы сил R≠0, то она приводится к 1й силе, т.е. к равнодействующей: а) R≠0, M0≠0 – в этом случае система приводится к равнодействующей, проходящей через центр т.О; б) M0≠0, R≠0 – вся система заменяется равнодействующей R’=R, проходящей ч/з т.С. Положение т.С определяется: расстояние ОС=d должно удовлетворять равенству R’d=|M0|. Знак момента относительно центра О силы R’ приложенной в т.С должен совпадать с моментом M0. m0(R’)=M0
|
|
|
24. Равновесие плоской системы сил
Необходимое и достаточное условие равновесия любой системы даются равенствами: R=0, M0=0 (главный вектор и главный момент равны 0)
1) основная форма условий равновесия Т.к. R=0, то его проекции тоже =0, Rx=0, RY=0. M0=0 – алгебраическая величина. Т.О – любая величина в пл-ти действия сил. {∑FKX=0; {∑FKY=0; {∑m0(FK)=0 (1) Для равновесия произвольной плоской системы необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов, относительно любого центра, лежащего в пл-ти действия сил были=0. 2) вторая форма условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех сил относительно каких-нибудь центров A и В и сумма их проэкций на ось х не перпендикулярную прямой АВ были =0. {∑FKX=0; {∑MA(FK)=0; {∑MB(FK)=0; (*) Докажем достаточность этих уравнений. Если для данной системы сил выполняется только два вторых условия: ∑MA(FK)=0; ∑MB(FK)=0 – такая сист сил может не находиться в равновесии, а иметь равнодействующую R, проходящую через т. А,В. Но по 1му условию ∑FKX=0. RХ=∑FKX=0, т.к. ось ОХ проведена не ┴ к АВ, то последнее условие (*) может быть выполнено только когда R=0, те.е имеет место равновесие. 3) третья форма условия равновесия (ур-е трех моментов) Для равновесия плоск сист сил необх и достаточно, чтобы суммы моментов относительно любых трех моментов А, В, С были=0. {∑MA(FK)=0; {∑MB(FK)=0; {∑MС(FK)=0 Необходимость этих условий как и в предыдущем случае – очевидна, т.к. нарушатся начальные условия. Следует из того, что если при одновременном выполнении данная система не находилась бы в равновесии, то она должна бы приводиться к равнодействующей, проходящей через т.А,В,С, что не возможно, т.к. точки не лежат на 1й прямой. #
25. Равновесие плоской системы параллельных сил.
В случае, когда все действующие на тело силы || друг другу можно направить на ось ох ┴ силе, а ось оу || силе. Тогда проекция каждой из сил на ось х будет =0 и первое равенство (1) превратится в тождество ∑FKX=0→ 0=0. В результате для системы параллельных сил останется только 2 условия из (1) {0=0; {∑FKY=0; {∑M0(FK)=0. Вторая форма условий равновесия будет иметь вид: {∑MA(FK)=0; {∑MB(FK)=0; При этом т.А и В не должны лежать на прямой || силам. AB не ||oy.
|
|
|
26. Центр тяжести.
27. Центр параллельных сил
Рассмотрим 2 параллельные силы F1 || F2, приложенные к телу в т. А и В. R=F1+F2. # R - Линия действия которой параллельна слагаемым силам и проходит ч/з некоторую т.С, лежащую на прямой АВ. Определим положение т.С с помощью теоремы Вариньона. mC®=mC(F1)+mC(F2). 0=F1h1+F2h2. F1/F2=h2/h1. В равенство входят модули сил, если силы повернуть около точек в одну и ту же сторону на один и тот же угол, то получатся 2 новые силы. Для них равенство сохранится. Линия действия их равнодействующей тоже пройдет ч/з т.С. Такая точка С называется центром параллельных сил F1 и F2. Для системы параллельных и одинаково направленных сил, приложенных к твердому телу равнодействующая всех сил проходит всегда через одну и ту же т.С, положение которой по отношению к т. приложения сил неизменно. Т.С ч/з которую проходит линия действия равнодействующей сист при любых поворотах этих сил около их точек приложения в одну и ту же сторону на 1й и тот же угол называется центром параллельных сил.
28. Координаты центра параллельных сил.
Возьмем произвольную сист коорд из осей x,y,z и точки A1,…An. R=∑Fn. Пользуясь тем, что положение т.С не зависит от направления сил повернем силы возле их точек риложения так, чтобы они стали параллельны оси oz и применим к силам теорему Вариньона. R=∑Fn. Так как R – равнодействующая F1…Fn, момент относительно оси оу = моменту относительно все сил. my®= ∑mY(Fn) { my(R)=R*xC; {my(F1)=F1*x1. R*xC=∑Fnxn. R*yC=∑Fnyn. R*zC=∑Fnzn. xC=∑Fnxn/R, yC=∑Fnyn/R, zC=∑Fnzn/R, где: R=∑Fn, где R=сумме всех сил. Эти ф-лы будут справедливы и для || сил, направленных в разные стороны, если считать, что Fn – алгебраические величины и если R≠0.
29. Центр тяжести твердого тела
Центром тяж-ти тверд тела наз-ся неизменно связанная с этим телом точка, через к-ю проходит линия действия равнодействующей сил тяжести, действующих на твердое тело при любом положениитела в пр-ве. Координаты центра тяжести равны: x=∑pixi/ p y=∑piyi/ p z=∑pizi/ p p=∑pi, где p=сумме pi, pi – сила тяжести отдельной частицы твердого тела. Согласно определения центра тяжести – центр тяж=ти точка геометрическая, она может лежать вне пределов данного тела.
30. Координаты центра тяжести однородных тел.
Для однородного тела вес PK его любой части пропорционален объему VK этой части. PK=j*VK. А вес Р всего тела пропорционален объему этого тела.P=jV, где j – единица объема. В результате пользуюсь этим можно написать xC=∑Vixi / V yC=∑Viyi / V zC=∑Vizi / V. Положение центра тяжести однородного тела зависит только от геометрической формы, а от величины j – не зависит. Если тело представляет собой однородную плоскую и тонкую пластину, то у нее: xC= ∑Sixi / S yC=∑Siyi / S. Координаты центра тяжести линии xC=∑Lixi // L yC=∑Liyi / L zC=∑Lizi / L, L=∑Li.
31. Способы определения координат центров тяжести.
1. Способ симметрии. Если однородное тело имеет плоскость, ось, или центр симметрии, то его центр тяжести лежит соответственно в пл-ти симметрии, на оси симметрии или в центре симметрии.
2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координату центра тяжести всего тела можно вычислить по формулам.
3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы. Если центры тяжести тела без выреза и с вырезом известны.
4. Интегрирование. Если тело нельзя разбить на несколько конечных частей, положение центра тяжести к-х известны, то тело разбивают на произвольно малые объемы VK, тогда координаты: xC= 1/V 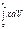 , yC=1/V
, yC=1/V 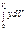 zC=1/V
zC=1/V 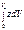
5. Экспериментальный метод. Центры тяжести неоднородных тел сложной конфигурации (машина,самолет…) можно определить экспериментально. Этот метод состоит в том, что тело подвешивают на нити или тросе за различные его части.
32. Кинематика точки и твердого тела
Введение в кинематику. Кинематика – раздел теоретической механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил. Время является скалярной величиной, непрерывно изменяющейся. В задачах кинематики t – время принимают за независимую переменную (аргумент). Все другие переменные величины – функции от времени t. t0=0c.
Основная задача кинематики точки и тверд тела состоит в том, чтобы зная закон движения точки (тела) установить методы определения всех кинематических величин, характеризующих данные движения. Траектория точки – непрерывная линия, которую описывает движущаяся точка, относительно данной системы отсчета. Если траектория является прямой линией, то движение – прямолинейное, иначе – криволинейное.
Задача кинематики твердого тела распадается на 2 части: 1) задание движения и кинематических характеристик движения тела в целом; 2) определение кинематических характеристик движения отдельных точек тела.
33. Способы задания движения точки.
1. Векторный. # Положение т.М в любой момент времени можно определить задав ее радиус-вектор, проведенный из начала координат. r=r(t), rX=x=ix rY=y=jy rZ=z=kz Введем единичные векторы r=ix+jy+kz.
2 .Координатный. Положение точки можно непосредственно определять ее декартовыми координатами (x,y,z), которые с течением времени при движении точки будут изменяться x=f(t), y=f(t), z=f(t). Эти уравнения представляют собой уравнения движения точки. Они определяют закон движения точки при координатном способе задания движения. Если задаие движения точки происходит все время в одной и той же пл-ти, то ур-е движения примут вид:x=f(t), y=f(t) (xoy). При прямолинейном движении точки, если вдоль ее траектории направить координатную ось,ее движение будет определяться одним ур-м. x=f(t). Н-р, {x=2t, {y=12t2. Движение т. задано уравнениями, t0=0, M0(0;0), t1=1c. M1(2,12) t=x/2 y=3x2 – траэктория движения т – парабола.
3. Естественный. Естественным способом задания движения т удобно пользоваться в тех случаях когда траектория движения заранее известна. # S=f(t) – закон движения т при его естественном способе задания движения. Пусть кривая АВ – траектория движения т. М относительно системы отсчета Oxyz. Положение т.М будет однозначно определяться криволинейной координатой S, которая равна расстоянию от Начальной точки O’ до т.М, измеренному вдоль дуги и взятому с соответствующим знаком. Т.о. чтобы задать движение естественным способом нужно знать: - траекторию движения; - начало отсчета с указанием “+” и “–“ направления отсчета; - закон движения вдоль т. S=f(t).
34. Вектор скорости точки.
Одной из основных кинематических характеристик движения т. является векторная величина, называемая – скорость точки. # Пусть движущаяся точка находится в момент времени t в положении М, определяемая радиус вектором r, а в момент времени t1 в положении М1, определяемое радиус вектором r1. Тогда за промежуток времени ∆t=t1-t, перемещение определяется вектором MM1 – вектор перемещения точки. Отношение вектора перемещения точки соответствующему промежутку времени даст векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени ∆t (V,r) VCP=MM1 / ∆t=∆r / ∆t ∆r=r1 Очевидно, что чем меньше промежуток времени ∆t, для которого вычислена VCP, тем точнее величина vCP будет характеризовать движение этой точки.
Скорость точки в данный момент времени – это векторная величина V,к которой стремится вектор величиной VCP при стремлении промежутка времени к 0.
V=lim(∆t-0)VCP
Вектор скорости в данный момент времени равен первой производной от радиус вектора по времени. V=dr/dt=r’
Вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону ее движения.
35. Вектор ускорения точки.
Ускорение т. наз-ся векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.
Пусть в некоторый момент времени t данная т. находится в положении М и обладает скоростью V,а в момент времени t1 и обладает скоростью V1.
Тогда за промежуток времени ∆t=t1-t скорость точки получит приращение ∆V. V1 всегда направлен в сторону вогнутости траектории. # Отношение приращения вектора скорости ∆V, соответствующего промежутку ∆t определяет вектор среднего ускорения т за этот промежуток. ∆V/∆t=aCP
Вектор среднего ускорения ↑↑ с вектором приращения скорости aCP VCP
Вектор ускорения в данный момент времени = 1й производной от вектора скорости или 2й производной от радиус вектора.
a= d2r / dt2 =dV / dt a=r”(t)=V’(t)
Вектор ускорения в общ случае направлен в сторону вогнутости траектории.
36. Определение скорости и ускорения точки при координатном способе.
Теорема: Проекция производной от вектора на ось неподвижную в данной системе отсчета равна производной от проекции дифференцируемого вектора на эту же ось.
1.Определение скорости точки. V=dr/dt rX=x rY=y rZ=z VX=drX/dt VX=x’ x=f(t) VY=drY/dt VY=y’ y=f(t) VZ=drZ/dt VZ=z’ z=f(t) Проекции скорости на координатные оси равны 1й производной от соответствующих координат по времени. Зная проекции сокрости найдем и ее направление V= 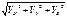 это значит определить углы между вектором и его проекциями cosα=VX/V cosβ=VY/V cosγ=VZ/V
это значит определить углы между вектором и его проекциями cosα=VX/V cosβ=VY/V cosγ=VZ/V
2.Определение ускорения точки aX=d2rX / dt2 =dVX /dt aX=x”=VX’ aY=d2rY / dt2 =dVY /dt aY=y”=VY’ aZ=d2rZ / dt2 =dVZ /dt aZ=z”=VZ’
Проекции ускорения т на координатные оси равны первым производным от проекции скорости или 2м производным от соответствующих координат по времени. a= 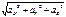 cosα=aX/a cosβ=aY/a cosγ=aZ/a
cosα=aX/a cosβ=aY/a cosγ=aZ/a
Касательное и нормальное ускорение точки Ускорение точки= геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и наз-ся касательным (тангенсальным) ускорением точки.
a=an+aτ aτ=d2S/dt2=dV/dt an=V2/R, R – радиус кривизны траектории в конкретный момент времени #
Проекция ускорения на касательную (тангенсальную) равна первой производной от числового значения скорости или 2й производной от расстояния (криволинейной координаты). Проэкция ускорения т на нормаль = квадрату скорости деленному на радиус кривизны траектории. a= 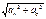
37. Частные случаи движения точки.
1. Прямолинейное R=∞. Касательная ускорения характеризует изменение числового значения скорости. an=0, a=aτ=dV/dt
2. Равномерное криволинейное V=const aτ=0, a=an=V2/R
3. Равномерное прямолинейное a=0.
S=Vt+at2/2
4. Равноускоренное криволинейное движение. Равнопеременное – такое криволинейное движение, при котором касательная ускорения остается все время постоянной. a=! t=0, S=S0, V=V0, a≠0 V=V0+at, S=S0+V0t+at2/2
5. Гармонические колебания. Точка совершает при этом движении колебания от +А до –А. Величина А= наибольшему отклонению точки от центра колебаний, амплитуда колебаний. Промежуток времени T=t1=2π/k, в течение которого точка совершает 1 полное колебание – период колебаний. При этом виде движения скорость и ускорение точки изменяются с течением времени по гармоническому закону.(Для повторяющихся операций) a=-Ak2*cos kt x=Acos kt x=Asin kt V= -Ak*sin kt
38. Поступательное движение
Поступательным называется такое движение твердого тела, при котором любая прямая проведенная в этом теле перемещается оставаясь параллельной своему первоначальному положению. Поступательное движение нельзя путать с прямолинейным. При поступательном траектории могут быть любые кривые линии.
Св-ва поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Рассм тело. Совершающее поступательное движении относительно системы отсчета Оxyz. # rB=rA+AB При этом длина АВ остается постоянной, как расстояние между т. твердого тела. Направление АВ остается неизменным, т.к. тело движется поступательно. drB/dt=drA/dt +d(AB)/dt VA=VB. скорости точек А и В в любой момент времени одинаковы по модулю и направлению. Следовательно, ускорения т. А и В в любой момент времени одинаковы по модулю и направлению. При поступательном движении общую для всех точек тела скорость, называют скоростью поступательного движения тела. А ускорение – ускорением поступательного движения тела. Вектора V и а можно изображать приложенными к любой т тела. Эти понятия имеют смысл только при поступательном движении тела.
39. Вращательное движение твердого тела вокруг оси. Угловая скорость и ускорение.
Вращательное движение ТВ тела вокруг какой-либо неподвижной оси называется такое движение тела, при к-м какие-нибудь 2 точки, принадлежащие телу (или неподвижно с ним связанные), остаются во все время движения неподвижными. Прямая, проходящая ч/з неподвижные т называется осью вращения. З-н вращательного движения тела вокруг неподвижной оси φ=f(t). Для определения положения вращающегося тела проведем ч/з ось вращения вдоль к-й направим ось AZ, неподвижную полуплоскость I и полуплоскость II, врезанную в само тело и совершающую вместе с телом вращательное движение. φ- угол поворота (радианы).
Основными кинематическими характеристиками вращ движения ТВ тела являются его угловая скорость и угловое ускорение. ω ε Числовое значение угловой скорости тела в данный момент времени = 1й производной от угла поворота по времени ω=dφ/ dt (рад/с, 1/с)
Угловую скорость тела можно изобразить в виде вектора ω, модуль которого равен |ω| и который направлен вдоль оси вращения тела в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки. Модуль |ω|
Угловое ускорение тела характеризует изменение с течением времени угловой скорости тела. ∆t=t1-t ∆ω=ω1-ω εCP=∆ω/∆t εCP=d2φ/dt=dω/dt=φ”=ω’ (1/с2) Числовое значение углового ускорения тела в данный момент времени равно 1й производной от угловой скорости или й производной от угла поворота тела по времени. [ε]=рад/с2. Если модуль угловой скорости со временем возрастает – вращение тела – ускоренное (ω и ε совпадают знаки), а если убывает – замедленным (ω и ε разные знаки).
40. Равномерное и равнопеременное вращение.
Если угловая скорость тела все время движения остается постоянной ω=const, то движение называется равномерным. Найдем закон равномерного вращения t=0, φ0=0, φ=φ0+ωt → φ=ωt. Найдем зависимость между n (частота вращения) и ω(1/с) 2πn= ωt ω=2πn/t (ω=2πn/60) ω=2πn – в секунду. Если угловое ускорение тела все время движения остается постоянным, то вращение называется равноперенным. Найдем закон равнопеременного движения (вращения) ω=ω0+εt, dφ=ω0dt+εtdt, φ=φ0+ωt+εt2
41. Скорости и ускорения точек вращающегося тела.
Рассм какую-нибудь т. М ТВ тела, находящуюся на расстоянии H от оси вращения. # Точка за время dt повернется на угол dφ. т.М совершает вдоль своей траектории элементарное перемещение dS=hd φ V= dS/ dt= hdφ/ dt → V=hω V – скорость в отличие от ω(угловой скор) иногда называют линейной или окружной скоростью т.М. Числовое значение линейной скорости точки вращающегося тела= произведению угловой скорости тела на расстояние от этой т до оси вращения. Скорость направлена по касательной к описываемой точкой окружности или ┴ пл-ти проходящей ч/з ось вращения. Скорости точек вращающегося тела пропорциональны их расстоянию до оси вращения #
Ускорения точек тела an=V2/h, aτ=dV/dt aτ=h dω/dt=hε an=h2ω2/h= hω2 Касательная составляющая ускорения aτ направлена по касательной к траектории (в сторону движения при ускоренном вращении тела, в обратную при замедленном). Нормальная составляющая всегда направлена по радиусу к оси (центру) вращения. a= 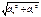 , a=
, a= 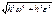 =h
=h 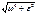 # Ускорение всех точек вращающегося тела пропорциональны их вращениям в данный момент времени и образуют в данный момент времени один и тот же угол α с радиусами описываемых ими окружностей.
# Ускорение всех точек вращающегося тела пропорциональны их вращениям в данный момент времени и образуют в данный момент времени один и тот же угол α с радиусами описываемых ими окружностей.
Векторы скорости и ускорения тела
Проведем из произвольной т.О оси АВ, радиус вектор r точки М. # Тогда h=rsin α V= ωrsin α |V|=| ω * r| - произведение модулей векторов. Вектор скорости любой т вращающегося ТВ тела равен векторному произведению угловой скорости тела на радиус вектор этой т. V= ωr – формула Эйлера. a=| ω V|*| ε r|, an= ωV, aτ= εr
42. Плоскопараллельное движение твердого тела.
43. Уравнение плоскопараллельного движения. Разложение движения на поступательное и вращательное.
Плоскопараллельным (плоским) наз-ся такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной пл-ти. # В дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости. Положение фигуры S в пл-ти Оху определяется положением какого-нибудь проведенного отрезка АВ. Положение отрезка АВ можно определить зная координаты xA, yA и угол φ,который отрезок АВ образует с осью Оx. Т.А выбранную для определения положения фигуры S, называют полюсом. {xA=f1(t); {yA=f2(t); {φ=f3(t) – уравнения движения плоской фигуры. # Движение плоской фигуры в ее плоскости может рассматриваться, как слагающаяся из поступательного движения, при котором все точки фигуры движутся также, как и полюс А, и вращательного движения вокруг этого полюса. Основными кинематическими хар-ками движения являются: скорость и ускорение поступательного движения = скорости и ускорению полюса: VA=Vn aA=aПОЛЮСА А также угловая скорость и угловое ускорение вращательного движения вокруг полюса. При изучении движения в кач-ве полюса можно выбирать любую точку фигуры. Вращательная часть движения не зависит от выбора полюса.
44. Определение траектории точек плоской фигуры.
# Рассм т М плоской фигуры, положение к-й определяется расстоянием АМ=В и углом ВАМ= α {x=xA+bcos(φ+ α), {y=yA+bsin(φ+ α), Эти равенства определяющие з-н движения т.М в пл-ти Оху, дают одновременно ур-я траектории этой точки в параметрическом виде. (т.к. сами ур-я заданы пар-ки)
45. Определение скорости точек плоской фигуры.
# r=rФ+rМ dr/dt=drA/dt + drM /dt V=VA+VM (относительн скорость) VM (ОТНОСИТ СК) =VA (переносная)+VМ отсоит А Скорость любой т плоск фигуры, геометрически складывается из скорости какой-либо т А, принятой за полюс, и скорости, к-ю точка получит при вращении относительно этого полюса. Модуль и направление скорости VM находится построением соответствующего параллелограмма. |VМА|= ω*АМ. VA=f(t) VA=S/t
46. Теорема о проекции скоростей двух точек тела.
Проекции скоростей двух точек твердого тела на ось, проходящую ч/з эти точки равны друг другу и сонаправлены. #
47. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.
МЦС – называется т пл фигуры, скорость которой в данный момент =0. Если фигура движется не поступательно, то такая т в кажд момент времени t существует и при том единственная. Пусть в момент времени t точки обладают скоростями: # Тогда т Р, лежащая на пересечении перпендикуляров Аа┴VA, Bb┴VB мгновенным центром скоростей, т.к. скорость в точке Р=0. VP=0. Скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг МЦС VA= ωPA VB= ωPB | VA/PA = VB/PB Скорости точек плоской фигуры пропорциональны их расстояниям от МЦС. Полученные рез-ты приводят к результатам: 1) Для определения МЦС надо знать только векторы скоростей VA VB каких-нибудь двух точек А и В плоской фигуры. 2) Для определения скорости любой точки плоской фигуры надо знать модуль и направление скорости какой-нибудь т А плоской фигуры и направление скорости другой ее точки В. 3) Угловая скорость ω плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь т фигуры к расстоянию от МЦС до нее. ω =Vb/PB
48. Определение ускорений точек плоской фигуры.
Ускорение любой т М плоской фигуры геометрически складывается из ускорения какой-нибудь другой т. А принятой за полюс и ускорения, к-е т М получит при вращении фигуры вокруг этого полюса. # aM=aA+aMA aMA=aMAn+aMAτ
49. Сложное движение точки.
50. Относительное, переносное и абсолютное движение.
Сложное движ тверд тела – абсолютное, относительное, перенсное движение.
1) Движение совершаемое т М по отношению к подвижной системе отсчета. Oxyz, называется относительным движением. Траектория АВ описываемая т в относительном движении, называется относительной траекторией. Скорость т М по отношению к осям Oxyz называется относительной скоростью и обозначается VOT. А ускорение – относительным ускорением аОТ #
2)Движение, совершаемое подвижной сист отсчета Oxyz (и все точки принадлежащие подв сист отсч) по отношению к неподвижной сист отсчета O1x1y1z1 VПЕР, апер Скорость той неподвижно связанной с подвижными осями Oxyz т. m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью т М в данный момент времени. Ускорение той неподвижно связанной с подвижными осями Oxyz т. m, с которой в данный момент времени совпадает движущаяся точка М, называется переносным ускорением т М в данный момент времени.
3) Движение, совершаемо т по отношению к неподвижной системе отсчета O 1x 1y 1z 1 называется абсолютным или сложным VАБ, аАБ Траектория CD этого движения называется абсолютной траекторией. Скорость – асбсолютн ск, ускорение – абс ускор.
Для решения соотв задач кинематики необходимо установить зависимости между относительными, переносными, абсолютными скоростями и ускорениями.
51. Теорема о сложении скоростей.
# Пусть т М совершает за промежуток ∆t=t1-t вдоль траектории АВ относительное перемещение, определяемое вектором ММ’. Сама кривая АВ двигаясь вместе с подвижными осями перейдет за тот же промежуток времени в новое положение A’B’. Одновременно та точка m кривой АВ с которой в данный момент времени совпадает т М, совершает переносное движение, определяемое вектором mm1. m принадлежит M, Mm1M1 mm1=Mm1, MM1=Mm1+m1M1 | ∆t Поделим обе части на ∆t и перейдем к пределу. lim(∆t-0)MM/∆t=lim(∆t-0)Mm1/ ∆t + lim(∆t-0) m1M1/ ∆t Исходя из определения lim(∆t-0)MM/∆t=VАБ lim(∆t-0)Mm1/ ∆t=VПЕР Так как при ∆t-0 кривая A’B’ стремится к кривой АВ - lim(∆t-0) m1M1/ ∆t=VОТ. VАБ =VОТ+VПЕР # При сложн движении VАБ= геом сумме относительн и переносной скоростей. Если угол между векторами VOTH и VПЕР обозначить как α, то модуль VАБ = 
52. Теорема о сложении ускорений (Теорема Кориолиса).
53 Вычисление относительного, переносного и кориолисова ускорений.
Найдем зависимость между относительным, переносным и абсолютным ускорением точки.
aАБ=dVАБ/dt = dVОТ/dt+dVПЕР/dt
Условимся,что изменение, к-е векторы VOT и VПЕР получают при относительном движении отмечать индексом 1, а при переносном движении индексом 2. aАБ=(dVОТ/dt) 1 – а ОТ + (dVОТ/dt) 2 +(dVПЕР/dt) 1+ ( dVПЕР/dt) 2 - аПЕР aАБ=aОТ +aПЕР +{(dVОТ/dt) 2 +(dVПЕР/dt) 1 } – aКОР
Величина, характеризующая изменение скорости при переносном движении и переносной скорости точки при ее относительном движении наз-ся поворотным или кориолисовым ускорением.
аАБ= аОТ+аПЕР+аКОР При сложном движении ускорение точки равно геом сумме 3х ускорений – относ, переносн и кориол.
Найдем формулировку для определения ускорения Кориолиса
Рассматривая общий случай будем считать переносное движение, т.е. движение подвижных осей Охуz, а с ними кривой АВ, слагающимися из поступательного движения вместе с некоторым полюсом и вращение вокруг этого полюса с угловой скоростью ω, называемой переносной угловой скоростью. dVOT/dt=VOT* ω При рассматриваемом переносном движении вектор VOT направлен по касательной кривой АВ. Переместится с этой кривой поступательно и одновременно повернется вокруг этой т m до положения VОТ 1 (dVOT) 2 =bb1= Vbdt {mb ω=Vb, mb=VOT} (dVOT)=VOT ωdt # # Определим (dVПЕР /dt) 1 Cкорость VПЕР= скорости той неизменно связанной с подвижными осями т m кривой АВ с к-й в данный момент времени совпадает М.
Проведем из т О радиус вектор, задающий положение т М Om=оМ VПЕР=V0+ ωr Совершим за промежуток времени ∆t относительн перемещение MM’=VOT*dt Точка придет в положение M’ для которого: V’пер=V0+ ω(r+MM’) Вследствие того, что точка совершает относительное перемещение MM’= VOT*dt вектор VПЕР получит приращение (dVПЕР) 1 =V’ПЕР –VПЕР = (V0+(r+MM’))+(V0+ ωr)= ωMM’= ωVOTdt aКОР=2(ωVOT)
Кориолисово ускорение = удвоенному векторному произведению переносной угловой скорости (ω – угл ск подвижной сист отсч) на относительную скорость точки.
Вычисление относительного, переносного и кориолисового ускорение: Относит ускорение вычисляется обычными методами кинематики точки: аОТ= an+aτ Переносное уск вычисляется,как ускорение точки некоторого твердого тела апер=аЦ+аВ= an+aτ=аХ+аY Кориолисово уск вычисляется по ф-ле aКОР=2(ωVOT) Модуль кориолисового уск, если угол между векторами ω и VOT обозначить за α, то модуль будет равен: aКОР=2|ω||VOT|sin α VОБ=VОБ Х+ VОБ Y
Направлен вектор ускорения Кориолиса также, как вектор произведения угловой скорости на относительную, т.е. ┴ пл-ти, проходящей ч/з векторы ω и VОТ, в ту сторону, откуда кратчайшее совмещение (ω VОТ) видно происходящим против часовой стрелки.
Правило Жуковского: Вектор относительной скорости Vr проецирем на пл-ть ┴ оси переносного вращения, получим проекцию, поворачиваем в данной пл-ти в направлении ωе на 90о.
53. Законы динамики. Задачи динамики материальной точки
Динамика – раздел теор механики, где изучается движение мат тел под действием сил. В динамике, в отличие от кинематики, при изучении движения тел принимают во внимание как действующие силы, так и инертность самих тел.
Инертность тела проявляется в том, что оно сохраняет свое движение при отсутствии действующих сил.
В классической механике масса m рассматривается, как величина скалярная, положительная и постоянная для каждого данного тела. Кроме суммарной массы движение тела зависит от формы тела (общий случай), точнее от взаимного расположения образующих его частей – от распределения массы в теле. При первоначальном изучении динамики вводят абстрактное понятие о материальной точке, как о точке обладающей массой.
З-ны динамики 1) Закон инерции Изолированная от внешних воздействий мат т сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое т при отсутствии сил – называется движением по инерции. З-н инерции отображает 1 из осн свойств материи – пребывать в неизменном состоянии. Система отсчета, в к-й справедлив з-н инерции – инерциальная система отсчета.
2) Осн закон динамики. Произведение массы мат точки на ускорение, к-е оно получило под действием данной силы = модулю этой силы, а направление ускорения совпадает с направлением этой силы. ma=F, a↑↑F
2й з-н динамики, как и первый имеет место только по отношению к ИСО. Если на точку действует одновременно несколько си, осн з-н динамики примет вид: ma=R ↔ ma= ∑Fi, R= ∑Fi
3) З-н действия и противодействия. Для 2х мат т он гласит: Две мат точки действуют друг на друга с силами равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные направления.
Задачи динамики: 1) Зная закон движения точки определить действующую на нее силу. 2) Зная действующую на тело силу, определить закон движения точки (осн задача динамики)
55. Основные виды сил.
1) Сила тяжести постоянная сила Р (G), действующая на любое тело, находящееся вблизи земной поверхности (≈50000 км) Модуль силы тяжести равен весу тела: P(G)=mg
2) Сила трения(скольжения – вязкое, сухое) Модуль силы трения определяется равенством FTP= fN, f - коэффициент трения, к-й будем считать постоянным. N – норм реакция опоры поверхности.
3) Сила тяготения (из з-на тяготения Ньютона) F=fm1m2/ r2, f – гравитационная постоянная, r – расстояние между мат точками. F= 6,67*10^(-11) м3/кг*с2.
4) Сила упругости(з-н Гука) Напряжение (сила, отнесенная к единице площади) пропорционально деформации F=cλ, F= σl, c, σ – коэффиц жесткости, λ, l – удлинение или сжатие.
5) Сила вязкого трения сила, зависящая от скорости, действует на тело при его медленном движении в очень вязкой среде. Сила выражается равенством: R=μV, μ – коэфф сопротивления, V – скорость тела.
6) Сила аэродинамического (гидродинамического) сопр – сила, действующая на тело, движущееся в такой среде, как воздух, вода, и зависящая от скорости. R=0,5 CX S ρ V2, ρ – плотность среды, S – площадь проекции тела на пл-ть, перпендикулярную направлению движения (площадь миделя), cX – безразмерный коэф сопротивления определяемый экспериментально и зависящий от формы тела и того, как оно ориентировано в движении.
56. Дифференциальные уравнения движения материальной точки.
Ур-я движения в декартовых координатах: {x=f1(t), {y=f2(t), {z=f3(t). ma=R=∑Fi Рассмотрим мат т, движущуюся под действием сил: F1,…Fn. a= d2r/dt2 R=RX+RY+RZ { maX=m d2x/dt2 =∑Fi x, maY=m d2y/dt2 =∑Fi y, maZ=m d2 z /dt2 =∑Fi z } – Диф ур-я движ мат т в прямоугольных Декарт коорд.
Д.У. в проекции на оси естеств трехгранника: # ma=∑Fi man = ∑Fni maτ = ∑Fτi aMB=0 {m V2/r = ∑ Fni, m dV/dt= ∑ Fτi } -д.у. движения т на оси естеств трехгранника
57. Общие теоремы динамики точки.
58. Количество движения точки. Импульс силы.
Кол-во движения мат т - векторная величина mV, равная произведению массы точки на ее скорость. Направление вектора mV такое же,как и скорость точки, т.е. по касательной к траектории.
Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени вводится понятие импульс силы.
Элементарный импульс силы называется векторная величина dS=F dt. Элем имп силы направлен вдоль линии действия силы. Импульс S любой силы F за конечный промежуток времени t1 вычисляется как предел интегральной суммы соответствующих элементарных импульсов S=0∫t Fdt Импульс силы за некоторый пром врем t1 равен опред интегралу от элемент импульса, взятому в пределах от 0 до t1.
59. Теорема об изменении количества движения точки.
Производная по времени от кол-ва движения точки равна сумме действующих на точку сил. m dV/dt= ∑Fi Пусть движущаяся точка имеет в момент времени t=0 скорость V0 и в момент времени t1 скорость v1. Умножим обе части равенства на dt и возьмем от них опред интегралы. V0V1∫m dV=0 t1∫∑F1dt mV1-mV0=∑Si. Изменение кол-ва движения точки за нек пром времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени. {mV1 Х-mV0 Х=∑Si Х mV1 Y -mV0 Y=∑Si Y mV1 Z-mV0 Z=∑Si Z }
60. Теорема об изменении момента количества движения точки (Теорема моментов).
Моментом кол-ва движения т относительно некоторого центра О называется векторная величина m0(mV), определяемая равенством m0(mV)=r*mV. # Вектор m0(mV) направлен перпендикулярно плоскости, проходящей через mV и центр О.
Момент кол-ва движения точки относительно какой-нибудь оси Oz, проходящей ч/з центр О будет равен проекции вектора m0(mV) на эту ось (моменты кол-ва движения от т О) mZ(mV)=|m0(mV)|Z=|m0(mV)|*cosγ производная по времени от момента кол-ва движения точки, взятого относительно какого-либо неподвижного центра равна моменту действующей на точку силы, относительно того же центра. Если момент действующей силы, относительно некоторого центра =0, то момент кол-ва движения т относительно этого центра есть величина постоянная. m0(F)=0, m0(mV)=const,
61. Работа силы. Мощность.
Для характеристики действия оказываемого силой на тело, при некотором перемещении вводится понятие о работе силы. Элементарные работы силы F, приложенные в т М, называется скалярная величина, равная ∂А=Fτ dS, где Fτ – проекция силы F на касательную Mτ к траектории т М, направленную в сторону перемещения этой т. Модуль элементарного перемещения т М. dS – элементарное перемещение.
Такое определение соответствует представлению о работе, как о мере того действия силы, к-е приводит к изменению модуля скорости точки.
Знак работы имеет следующий смысл: Работа «+», когда составляющая Fτ направлена в сторону движения (сила ускоряет движение). Работа «-», когда Fτ противоположна направлению движения(сила замедляет движение)
Элементарная работа силы= скалярному произведению силы на вектор элементарного перемещения точки в т. ее приложения.
dA=FXdx+FYdy+FZdz Можем записать: Работа силы на любом перемещении M0M1 = взятому вдоль этого перемещения интегралу от элементарной работы A(M0M1)=M0 M1∫FXdx+FYdy+FZdz
Мощность величина, определяющая работу, совершаемая силой в единицу времени. V=A/t – равномерное движение N=dA/dt= Fτ dS/dt = FτV
Мощность – произведение касательной составляющей силы на скорость. В технике за единицу мощности применяются ЛС (лошадиные силы) 1ЛС=736 Вт Работу произведенную машиной можно измерять произведением ее мощности на время работы – кВт*ч
62. Теорема об изменении кинетической энергии точки.
Кинетич энергия т – скалярная величина: mV2/2, равная половине произведения массы на квадрат скорости. EK= mV2/2
Рассмотрим мат т с массой m. Из положения М0 перемещающуюся в т Мi со скоростью Vi в этой точке.
maτ= ∑Fτ i, aτ=V* dV/dS, aτ=dV/dt *dS/dS= mV*dV/dS= ∑Fτ i | ∑ dAi= ∑Fτi*dS mV dV= ∑dAi d(mV2/2)=∑dAi mV2i / 2 – mV20 / 2= ∑A(M1M0) Изменение кинетич энергии т при некотором ее перемещении равно алгебраич сумме работ всех действующих на точку сил на том же перемещении.
63. Прямолинейные колебания точки
64. Свободные колебания без учета сил сопротивления.
Рассмотрим т М, движущуюся прямолинейно под действием только 1й восстанавливающей силы f направленной к неподвижному центру О и пропорциональной расстоянию от этого центра # Сила F стремится вернуть т в равновесное положение О, где F=0, отсюда и наименование – восстанавливающая сила. FX= -cx, где c –коэфф пропорциональности, maX= ∑FX=FX, т.е. 1 сила aX=x” разделим обе части на m, с/m=k2 – введем обозначения x”+k2x=0 – диф ур-е свободных колебаний при отсутствии сопротивления.
Колебания, совершаемые т по з-ну x=Asin(kt+α) – называется гармоническими. Св-ва своб кол-й: 1) Амплитуда и начальная фаза колебаний зависит от начальных условий. 2) Частота k, а следовательно и период колебаний от начальных условий не зависят и являются неизменными хар-ками данной колеблющейся сист.
65. Свободные колебания при вязком сопротивлении. (Затухающие колебания).
Пусть на точку при ее движении действует восстанавливающая сила F и сила сопротивления R. R= μV, Тогда: FX= -cx mx”= -cx- μV разделим на m: x”+bx’+k2x=0, где μ/m=b, x’=V – д.у. своб кол-й при сопротивлении пропорциональном скорости.
66. Общие свойства вынужденных колебаний.
Рассм случай колебаний, когда на т кроме восст силы F действует еще периодически изменяющаяся со временем сила Q. Проекция которой на ось ox равна QX=Q*sin pt. Эта сила – возмущающая сила – гармоническая. А колебания происходящие при действии такой силы – вынужденные. Величина p является частотой возмущающей силы (с силой сопротивления и без) 1) при отсутствии сопротивления вынужд кол-я – только восстанавливающая сила FX= -cx. QX=Q0 sin pt, mx”=-cx+Q0 sin pt, x”+k2x=p0sin pt – (з-н движ вын кол-й) д.у. вынужд кол-й т при отсутствии сопротивления. k=p – частота вынуждающей силы= частоте собственных колебаний – резонанс, + (радиотехнека) и – (обвал моста). 2) вынужд колебания при вязком сопротивлении Рассм движение т на к-ю действует восстан сила F, сила сопротивления R и возмущающая сила Q. mx= -cx- μx”+Q0sin pt x”+bx’+k2x=P0sin pt – д.у. вынужденных кол-й при наличии вязкого сопротивления.
Общие свойства вынужденных колебаний: 1) Амплитуда вынужденных колебаний от начальных условий не зависит. 2) Вынужд кол-я при наличии сопротивления не затухают. 3) Частота вынужденных колебаний = частоте возмущающей силы и от характеристик колеблющейся системы не зависит. (возмущающая сила «навязывает» системе свою частоту колебаний) 4) Даже при малой Q (возмущающей силе) можно получить интенсивные вынужденные колебания, если сопротивление мало, а частота р (возмущающей силы) близка к k (p≈k) 5) даже при больших значениях возмущающей силы вынужденные колебания можно сделать скольугодно малыми (p>>k)
67. Динамика системы.
68. Механическая система. Внешние и внутренние силы.
Системы мат т или тел, движение (равновесие) к-х рассматривается –т будем называть механической системой. Внешними силами называют действующие точки системы, со стороны точек или тел, не входящих в состав данной сист. Внутренними силами наз-ют силы, с которыми т или тела действуют друг на друга. Св-ва внутр сил: 1) Геом сумма всех внутр сил (главный вектор) равняется 0 2) Сумма моментов – гл момент системы всех внутренних сил, относительно любого центра или оси =0.
69. Масса системы. Центр масс.
Масса сист= арифм сумме масс всех точек, или тел, образующих эту сист. M(m)n M= ∑mi, i=1n. xC= ∑mixi/ ∑M, yC= ∑miyi/ ∑M M*rC= ∑miri Геом т С, координаты к-й определены формулами центра тяжести, наз-ся центром масс или центром инерции механической системы. xC=1/M ∑mkxk yC=1/M ∑mkyk rC=1/M ∑mkrk - если положение т задать радиус-вектором.
70. Момент инерции тела относительно оси
Моментом инерции тела, относительно данной оси oZ (или осевым моментом инерции) наз-ся скалярная величина = сумме произведений масс всех точек тела на квадраты их расстояний от этой оси. JZ= ∑mih2i Осевой момент инерции является мерой инертности тела при вращательном движении. (при поступательном - масса). Радиусом инерции тела, относительно оси oz наз-ся линейная величина определяемая равенством JZ=Mρ2Z, ρZ – радиус инерции. Радиус инерции геометрически равен расстоянию от оси oz до той точки тела,в к-й нужно сосредоточить всю массу тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
71. Моменты инерции некоторых однородных тел.
Тонкий однородный стержень: JZ=M l2/ 3 (посередине ось), JZ=M l2/ 12 (ось через конец проходит)
Тонкое круглое однородное кольцо JC=M R2
Тонкая круглая пластина, диск JC=M R2 /2
Прямоугольная пластина JY=M a2/3
Момент инерции конуса JC=0,3 M R2
Момент инерции шара JC=0,4 M R2.
72. Теорема о движении центра масс.
|
|
|


