 |
Применение теоремы Гаусса для расчета электростатических полей
|
|
|
|
Билет № 3
Потенциал поля.
Силы электростатического поля консервативные т.е. независимые от траектории движения заряда.
F=- gradП
Fx= -¶П/¶x аналогич Fy и Fz
1) F= - dП/dr
Для электростатич. сил F=f(r). Воспользуемся этой зависемостью для введения третей характеристики поля - потенцеала. Преобр. 1) 2) dП= - Fdr F - куллоновская сила взаимодействия между двумя точечн. зарядами q и q0.
F=k(÷qq0÷/r2) Подставим F в 2) и проинтегрируем лев. и прав. часть.
3) òdП=ò -k(÷qq0÷/r2)dr из 3)
П= -k÷qq0÷òdr/r2=
=k÷qq0÷´(1/r)+C
Разделим лев. и прав. часть 4) на q0.
5) j=П/q0=(1/4pe0 )´(q/r)+C
6) j=П/q0 Потенцеал поля в данной точке численно равен потенцеальной энерии пробного заряда помещенного в данную точку.
[j]=B=Дж/К
7) j=(1/4pe0 )´(q/r) при j=0 r®¥, j ~ d при r=const,
j ~1/r при q=const
При q>0 j>0 +
При q<0 j<0 -
Связь между напряженностью поля и потенциалом в дифференциальной форме.
Для получения связи между Е и j в одной точке воспользуемся выражением для элементарной работы при перемещении q0 на dl по произвол. траектории.
dA=q0Eldl
В силу потенциального характера сил электростатического поля эта работа совершается за счет убыли потенциальной энергии.
dA= - q0 dj = - П
Eldl = - dj
3) El= - (dj /dl)
Проекция вектора напряженности поля на произвольном направлении (l) равна взятой с обратным знаком производной по этому направлению.
4) Ex= - (dj /dx)
Ey= - (dj /dy) Ez= - (dj /dz)
_ _ _
E= - (i (¶/¶x)+j (¶/¶y)+
_
+k (¶/¶z))´j
E= -grad
Напряженность поля в данной т. равна взятому с обратным знаком градиенту потенциала в этой точке.
Градиент скалярной функции является вектором.
Градиент показывает быстроту изменения потенциала и направлен в сторону увеличения потенциала.
Билет № 4
Теорема Гаусса в отсутствии диэлектрика (вакуум): поток вектора E
|
|
|
через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов Σ q, охватываемых этой поверхностью, и деленной на ε0
Применение теоремы Гаусса для расчета электростатических полей
В случае электростатических полей, обладающих той или иной
симметрией (осевая и сферическая симметрия, однородное поле), теорема
Гаусса позволяет достаточно просто получить выражение для модуля
вектора E. При применении теоремы Гаусса выделяют следующие этапы:
1) изсимметрии распределения зарядов определяют направление вектора E вкаждой точке поля;
2) выбирают произвольную замкнутую поверхность ирассчитывают поток вектора E через нее. Поверхность должна содержатьвнутри себя заряд (часть заряда), создающий поле, и отражать симметрию поля(цилиндр, сфера);
3) рассчитывают заряд, попадающий внутрь поверхности;
4)применяют теорему Гаусса для определения модуля вектора E.
Рассмотрим конкретные пример применения теоремы Гаусса.
Пример. Поле равномерно заряженной бесконечно длинной
прямолинейной нити.
1 этап. Введем линейную плотность τ заряда нити. Для этого на
заряженной нити выбираем элемент длины dl, содержащей заряд dq, и
рассчитываем τ по формуле 
т.е. τ представляет собой заряд, приходящийся на единицу длины нити.
Для равномерно заряженной нити во всех ее точках τ будет одинаковой
(τ = const), поэтому поле такой нити обладает осевой симметрией - линии E
представляют собой прямые, выходящие из нити и лежащие в плоскостях,
перпендикулярных к ней (рис.а). Причем на одинаковых расстояниях от
нити, т.е. на цилиндрических поверхностях, модуль E будет одинаковым.
2 этап. Выбираем замкнутую поверхность в виде цилиндра, имеющего
высоту H и радиус r, ось цилиндра совпадает с нитью. Поток E Φ через
основания цилиндра равен нулю (α=900), поэтому остается поток только через его боковую поверхность
|
|
|
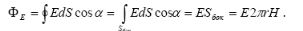
3 этап. Рассчитываем заряд отрезка нити длины Н, попадающий внутрь
цилиндра,
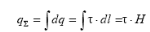
4 этап. Применяем теорему Гаусса для расчета модуля вектора E
(2)
Формула (2) позволяет оценить разность потенциалов между двумя
точками, находящимися на расстоянии r1 и r2 от нити (рис.а).
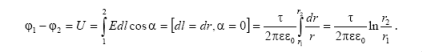
На рис.б приведен график зависимости модуля вектора E поля нити
от расстояния r до нее
Билет № 6
 | ||
 |
Законы сохранения.
Закон сохранен. энергии
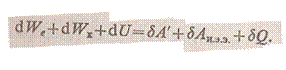Будем считать, как это обычно бывает, что в рассматриваемых процессах температура системы поддерживается постоянной, а изменение плотности диэлектриков и теплота, выделяющаяся или поглощающаяся в них при изменении вх поляризован-ности, пренебрежимо малы. В таком случае можно считать, что dU=0 и dQ== — dQ д-л, т. е. что от системы отводится только теплота Джоуля — Ленца, которая выделяется электрическими токами, связанными с перераспределением зарядов в проводниках системы. Подставив эти значения dQ и d Q в уравнение,
 |
получим выражение закона сохранения
Закон сохранения заряда
Алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяются при любых процессах, происходящих в этой системе.
Билет №7
|
|
|
