Напряженность Поле у поверхн. заряж. проводника.

Рассм. произаольную форму проводника заряж. по поверх. с поверхностной плотностью s.

Воспольз. теор. Гаусса в интегральной форме.

òDdS=Sq_i

^s

На заряж. поверхности отсечем круг площадью S.

òe₀EdS=e₀EòdS

^{s s}

e₀E´S=s´S

в т. А E=s/e₀

D=e₀E D=s

Напр. поля прямопропорц. поверх. плотности заряда проводника в окрестностях этой точке.

Разделение зар. по проводнику завис. от его поверх. (у острых углов заряд больше, напряж. сильнее).

 

 

Билет № 13

Электрическая ёмкость уединённого проводника и конденсатора: уединенным проводником наз. проводник, который находится столь далеко от других тел, что влиянием их электриче­ских полей можно пренебречь. Характер распределения зарядов по поверхности за­ряженного уединенного проводника, нахо­дящегося в однородной, изотропной диэлек­трической среде, зависит только от формы поверхности проводника. R£r£¥; E=k×(Q/r²); j_ш=k×(Q/R_ш); j=k×(Q/r), где k=k(x,y,z) – функция координат точки A, зависящая от формы и размеров поверхности. Q=4pee₀R_шj_ш, где 4pee₀R_ш=С. Величина С, равная отношению заря­да q уединенного проводника к его потен­циалу j, наз. электрической ем­костью этого проводника (при j=0 в бесконечно удалённой точке): C=Q/j. [C] – фарад, 1Ф=1Кл/1В. Электроемкость уединенного проводни­ка зависит от его формы и размеров. Потенциалы одинаково заряжен­ных и геометрически подобных проводников обратно пропорциональны их линейным размерам, а электроемкости этих проводни­ков ~ им. Электроемкость уединенного проводни­ка зависит также от диэлектрических свойств окружающей его среды. Ни от материала проводника, ни от фор­мы и размеров возможных полостей внутри проводника его электроемкость не зависит, так как свободные заряды находятся только на внешней поверхности проводника. j_R= ò^¥ _RE­_rdr, где j¯, а C­. Электроемкость неуединенного проводника всегда больше электроемкости того же про­водника, когда он уединен. Плоский конденсатор сост. из двух || металлических пластин пло­щадью S каждая, расположенных на близ­ком расстоянии d одна от другой. Заряды пластин q>0 и –q. Если линейные разме­ры пластин велики по сравнению с d, то электростатическое поле между пластинами можно считать таким же, как поле между двумя плоскостями, заряженными разнои­менно с поверхностными плотностями заря­дов s=q/S и –s. Если ось ОХ проведена ^ пластинам конденса­тора в направлении от положительно заря­женной пластины 1 (х₁=0) к отрицатель­но заряженной пластине 2 (x₂=d}, то напряженность поля конденсатора между пластинами Е_x=s/ee₀(0£x£d), где e – относительная диэлектрическая проницаемость среды, заполняющей кон­денсатор. Т. к. dj/dx=–E_x=–s/ee₀ то разность потенциалов пластин j₂–j₁=–(s/ee₀) ò ^d₀dx=–sd/ee₀=

=–qd/ee₀S. Т. о., электрическая емкость плоского конденсатора С=q/j₁–j₂=ee₀S/d. Формула справедлива только при малых значениях расстояния d между пластинами (d<<ÖS), когда можно прене­бречь нарушением однородности электро­статического поля у краев пластин. Сферический конденсатор сост. из двух концентрических металлических об­кладок 1 и 2 сферической формы, радиусы которых соотв. равны R₁, и R₂>R₁. Пусть q>0 – заряд обкладки 1, а –q – заряд обкладки 2. Равномерно заряженная сфера создает электростатическое поле только в области пространства вне этой сферы. Вне наружной обкладки поля разноименно заря­женных обкладок взаимно уничтожаются, а поле внутри конденсатора, т.е. между обкладками, создается только заря­дом q внутренней обкладки. Напряжённость поля в конденсаторе направлена радиально: Е=Е _r, причём E _r =q/4pee₀ r ², где e – относительная диэлектрическая проницаемость среды, заполняющей кон­денсатор. Т. к. dj/d r =–E _r =–q/4pee₀ r ², то разность потенциалов обкладок j₂–j₁=–q/4pee₀ ò ^R2_R1d r / r ²=q/4pee₀((1/R₂)–(1/R₁)). Электрическая ёмкость сферического конденсатора: C=q/j₁–j₂=4pee₀/(1/R₁)–(1/R₂)= =4pee₀R₁R₂/R₂–R₁ [1]. При R₂®¥ конденсатор превращается в уединенную сферу радиуса R₁, а электри­ческая ёмкость конденсатора приближается по значению к электрической емкости уеди­нённой внутренней обкладки С₁=4pee₀R₁. При любом конечном значении R₂ электри­ческая емкость сферического конденсатора больше электрической емкости одной уеди­ненной его внутренней обкладки. Если R₂–R₁=d<<R₁, то из формулы [1] сле­дует, что C»ee₀S/d, где S=4pR²₁ – пло­щадь внутренней обкладки. Цилиндрический конденсатор сост. из двух соосных тонкостенных металлических цилиндров высотой h и радиусов R₁и R₂>R₁, вставленных друг в друга. Пусть заряд внутренней обкладки радиуса R₁q>0, а внешней –q. Если h>>(R₁ и R₂), то, пренебрегая искажениями поля вблизи кра­ев конденсатора, можно приближенно счи­тать, что поле конденсатора такое же, как поле двух соосных цилиндров бесконечной длины, заряженных с линейными плотностями зарядов t=q/h и –t. Внутри конденса­тора поле создается только внутренней обкладкой. Из s=t/(2pR₁)q/(2pR₁h), следует, что напряженность поля в диэлектрике с относи­тельной диэлектрической проницаемо­стью e, заполняющем поле между обклад­ками конденсатора (R₁£r£R₂), равна E _r =q/(2pee₀h r). Т. к. dj/d r =–E _r =–q×1/2pee₀h× r, то разность потенциалов обкладок конден­сатора j₂–j₁=

=–q/2pee₀h ò ^R2_R1d r / r =–(q/2pee₀h)ln(R₁–R₂). Электрическая ёмкость цилиндрического конденсатора C=q/j₁–j₂=2pee₀h/ln(R₂/R₁). Если зазор между обкладками конден­сатора d=(R₂–R₁)<<R₁, то ln (R₂/R₁)=ln(1+d/R₁)»d/R₁ и C»ee₀S/d, где S=2pR₁h – площадь внутренней обкладки. При || соединении конденсаторов их общая С=åС_i. При последовательном соединении к. величина, обратная электрической ёмкости батареи = å величин, обратных электрическим ёмкостям всех конденсаторов, которые входят в батарею.

 

Билет №14

Энергия заряженного проводника, конденсатора, системы проводников и зарядов. Энергия электростатического поля: Сообщение проводнику электрического заряда связано с совершением работы по преодолению кулоновских сил отталкивания между одноименными зарядами. Эта работа идет на увеличение электрической энергии заряженного проводника. Элементарная ра­бота dА', совершаемая внешними силами при перенесении малого заряда dq из беско­нечности на уединенный проводник, равна:

dА'=j dq=Cj dj, где С и j – электроемкость проводника и его потенциал, начало отсчета которого выбрано в бесконечно удаленной точке.

Работа, совершаемая при увеличении потенциала проводника от 0 до j, т. е. при сообщении проводнику заряда q=Сj, равна: A'= ò ^j₀Cj dj=Cj²/2, =>, энергия заря­женного конденсатора. Если q – заряд кон­денсатора, а Dj=j₁–j₂ – разность потенциалов положительно и отрицательно заряженных его обкладок 1⁺ и ­2^– то для переноса малого заряда dq с обкладки 2 на обкладку 1 внешние силы должны совер­шить работу dA'=(j₁–j₂)dq=q dq/C. Ра­бота внешних сил при увеличении заряда конденсатора от 0 до q равна: A'= ò ^q₀q dq/C=q²/2C. =>, электрическая энергия заряженного конденсатора:

W_e= q²/2C=C(j₁–j₂)²/2=q(j₁–j₂)/2. Учитывая, что конденсатор – это систе­ма из двух проводников 1 и 2, заряды кото­рых q₁=q и q₂=–q, =>, W_e=½(q₁j₁–q₂j₂). Электрическая энергия системы из n неподвижных заря­женных проводников равна W_e=½åq_ij_i, где q_i – заряд i-го проводника, а j_i – его потенциал (относительно бесконечно уда­ленной точки) в электростатическом поле всей системы из n проводников. q_i= ò _(Si)s_idS, где s_i, – поверхностная плотность свобод­ных зарядов на малом элементе поверхно­сти i-го проводника площадью dS. =>, W_e=½å ò _(Si)j_is_idS

 

Магнитное поле - особая форма существования материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами. Магнитное поле:

- является формой электромагнитного поля;

- непрерывно в пространстве;

- порождается движущимися зарядами;

- обнаруживается по действию на движущиеся заряды;

- описывается уравнениями Максвелла.

Энергия магнитного поля - энергия, связанная с магнитным полем и преобразующаяся в другие формы энергии при изменении магнитного поля.

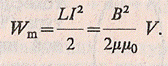Электрическое поле - особая форма существования материи, посредством которой осуществляется взаимодействие между покоящимися или движущимися электрическими зарядами.

Энергия Электрического пол я:

 

 

Электромагнитное поле - особый вид материи:

- посредством которого осуществляются электромагнитные взаимодействия;

- представляющий собой единство электрического и магнитного полей.

В каждой точке электромагнитное поле характеризуется:

- напряженностью и потенциалом электрического поля; а также

- индукцией магнитного поля.

Энергия электромагнитного поля W _{Эл. маг} = W_e +W_m

Билет № 15

Объёмная плот­ность энергии электростатического поля (для однородных и неоднородных полей): w _e=dW_e/dV=½ee₀E²=½ED, где D=ee₀E, а dW_e – энергия малого элемента dV объема поля, в пределах которого величину w _e можно считать всюду одинаковой. Энергия электростатического (однородного и неоднородного) поля: W_e= ò _(Vполя)(ee₀E²/2)dV= ò _(Vполя)(DE/2)dV.

Билет № 16

Постоянный электрический ток -электрический ток, не изменяющийся с течением времени по силе и направлению I=q/t

Для постоянства электрического тока проводимости необходимо, чтобы напряженность электрического поля во всех точках проводника, по которому идет этот ток, сохранялась не изменой. Поэтому заряды не должны накапливаться или убывать где-либо в проводнике, по которому идет постоянный электрический ток. В противном случае изменялось бы электрическое поле этих зарядов. Указанное условие означает, что цепь постоянного тока должна быть замкнутой, а сила тока – одинаковой во всех поперечных сечениях цепи.

Закон Ома:

Сила тока,протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах: I= U / R

Закон Видемана-Франца:

Для всех металлов при одной и той же температуре отношение теплопроводимости K к удельной электрической проводимости g

K/g = C

Друде в 1900 году построил первую классическую теорию проводимости металлов, основанную на представлении о газе свободных электронов.

Основные положения теории

1) Электропроводность металлов обусловлена большим количеством носителей зарядов – электронов. Их совокупность рассматривают как электронный газ, подчиняющийся законам идеального газа. Вследствие сильного взаимодействия между атомами металла при соединении последних в кристаллическое твердое тело, самые внешние их электроны перестают быть связанными с отдельными атомами и легко переходят от одного атома к соседнему и далее через всю кристаллическую решетку. В узлах кристаллической решетки располагаются положительные ионы металла, а между ними хаотически движутся свободные электроны.

2) Вводится характеристика λ – средняя длина свободного пробега электронов, которая по порядку величины равна периоду кристаллической решетки металла 10–10 м.

3) Пользуясь закономерностями кинетической теории газов, можно определить среднюю кинетическую энергию теплового движения электронов

где m − масса электрона; v кв– средняя квадратичная скорость, определяемая классическим распределением Максвелла электронов по скоростям.

При T = 273 К 5 v кв ≈ 10 м/с, таков же порядок средней арифметической скорости. Тепловое движения электронов хаотично, как и молекул газа, поэтому оно не может привести к возникновению электрического тока.

4) Упорядоченное движение электронов, т.е. электрический ток, создается лишь под действием внешнего электрического поля. При этом скорость направленного движения (дрейфа) электронов v ≈ 8⋅10−4 м/с очень мала по сравнению со скоростями теплового движения при обычных температурах,

что объясняется частыми столкновениями электронов с ионами кристаллической решетки.

5) Практически одновременное начало движения электронов по проводнику объясняется мгновенным (со скоростью света c = 3⋅108 м/c) распространением вдоль проводника электромагнитного поля.

Билет № 17

Разность потенциалов - скалярная величина, равная отношению работы электрического поля по перемещению положительного заряда из одной точки поля в другую точку к величине этого заряда. В СИ разность потенциалов измеряется в вольтах.

(j₁- j₂)= A\ q

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: