Связь систем замыканий с операторами замыкания

Основные понятия и примеры

 

Понятие упорядоченного множества является фундаментальным для современной теоретико-множественной математики, поэтому первым делом ведём именно это понятие и понятия с ним связанные.

Определение 1. Пусть L – непустое множество с бинарным отношением , которое является рефлексивным, транзитивным и антисимметричным. Тогда введенное отношение – отношение порядка. Множество L – упорядоченное множество.

Определение 2. Упорядоченное множество, в котором два элемента сравнимы, называется линейно-упорядоченным множеством или цепью.

Определение 3. Решеткой называется упорядоченное множество, в котором любые два элемента имеют точную верхнюю и точную нижнюю грани.

В качестве второго шага введём те определения и предложения, которые непосредственно связаны с темой дипломной работы и которыми будем пользоваться в дальнейшем.

Определение 4. Пусть A – произвольное множество и B (A) – его булеан, то есть множество всех его подмножеств. Будем рассматривать некоторые подмножества булеана B (A), или системы подмножеств множества A. Система D подмножеств множества A называется системой замыканий, если само множество A принадлежит D и система D замкнута относительно пересечений, то есть

∩ Y D для любой непустой подсистемы Y D.

Так как система замыканий замкнута относительно произвольных пересечений, то из предложения 1 следует, что система замыканий является полной решеткой (относительно упорядоченности по включению). Но это не обязательно подрешетка в B (A), так как операция объединения в D, вообще говоря, отлична от этой операции в B (A).

Одним из примеров системы замыканий является следующий:

Пример 1.1:   Система всех подгрупп группы G является системой замыканий, так как G является подгруппой в G и пересечение любого непустого семейства подгрупп группы G само будет подгруппой в G.

Введем ещё одно важное понятие – понятие оператора замыкания на множестве.

Определение 5. Оператором замыкания на множестве A называется отображение  множества B (A) в себя, которое подчиняется следующим трём аксиомам:

J. 1. X (X);

J. 2. Если , то (X) (Y);

J. 3. (X) = (X)

для всех X, Y B (A).

Для каждой системы замыканий D на множестве A можно определить оператор замыкания  равенством

(X) = ∩{ Y D | Y X } для всех X A.

Отметим, что группа аксиом J. 1 – J. 3 является независимой. Покажем это.

Приведём пример отображения, при котором выполняются аксиомы J. 2, J. 3, а аксиома J. 1 не выполняется. Каждому подмножеству X множества A поставим в соответствие пустое множество. Очевидно, что при таком задании оператора не выполняется лишь первая аксиома.

Отображение , при котором выполняются только аксиомы J. 1, J. 2, определим так. Пусть A = { a, b, c }, опишем оператор  следующим образом: каждому элементу поставим в соответствие множество, состоящее из самого этого элемента и элемента, находящегося рядом с ним. Пустое и само множество A при этом отображении переходят в себя:

, A A;

{ a } { a, b }, { b } A, { c } { b, c };

{ a, b } A, { a, c } A, { b, c } A.

Очевидно, что первая и вторая аксиомы выполняются, а третья не выполняется, так как (a) = A ≠{ a, b } = (a).

Пример отображения, при котором не выполняется только аксиома J. 2 следующий. Пусть A = { a, b, c }. Отображение  зададим так: пустое, все двухэлементные подмножества и само множество A переходят в себя, а всем одноэлементным подмножествам поставим в соответствие множество A:

, A A;

{ a } A, { b } A, { c } A;

{ a, b } { a, b }, { a, c } { a, c }, { b, c } { b, c }.

Очевидно, что аксиома J. 2 не выполняется, так как { a } { a, b }, но ({ a }) = A 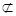{ a, b } = ({ a, b }).

Следовательно, мы показали, что система аксиом J. 1 – J. 3 будет независима.

Одним из видов операторов замыкания является алгебраический оператор замыкания. Дадим определение.

Определение 6. Оператор замыкания  на множестве A называется алгебраическим, если для любых X A и a A

а (X) влечет a (F)

для некоторого конечного подмножества F множества X.

С определением алгебраического оператора замыкания тесно связано понятие алгебраической системы замыканий.

Определение 7. Система замыканий D на множестве A называется алгебраической, если соответствующий оператор замыкания  является алгебраическим, то есть для любого X A

a { D D: X D} влечёт a { D D: F D}

для некоторого конечного F X.

Приведём один из наиболее важных примеров оператора замыкания, который широко применяется в топологии. Этот оператор ставит в соответствие каждому подмножеству X топологического пространства A его замыкание.

Пример 1.2: Пусть  – топологическое пространство. Введем на множестве A отображение , заданное следующим образом: X [ X ], где [ X ] – замыкание множества X A. Покажем, что  – оператор замыкания на множестве A.

Для этого проверим выполнимость свойств J. 1 – J. 3.

1) Если X Y, то [ X ] [ Y ].

Возьмем x ₀ [ X ]. Тогда любая окрестность точки x ₀ содержит точки множества X в любой окрестности точки x ₀ содержатся точки множества Y x ₀ [ Y ].

2) X [ X ].

Каждая точка множества является его точкой прикосновения. Значит, каждая точка множества X лежит и в [ X ].

3) [[ X ]] = [ X ]. Докажем методом двойного включения.

a) [ X ] [[ X ]]. Доказано во втором пункте.

b) x ₀ [[ X ]] Возьмем U (x ₀), для неё y ₀ U (x ₀) [ X ] y – точка прикосновения множества X U (y ₀) найдутся точки множества X. Возьмем U (y ₀) U (x ₀), z ₀ U (y ₀) X. Отсюда z ₀ U (x ₀) X. Тогда x ₀ – точка прикосновения множества X x ₀ [ X ]. Таким образом, [[ X ]] [ X ].

Пример 1.3:   Каждому множеству X точек плоскости A = R ² поставим в соответствие его выпуклую оболочку . Ясно, что X  оператор замыкания на множестве A.

Предложение 1. Если A – такое упорядоченное множество с наибольшим элементом, в котором каждое подмножество обладает точной нижней гранью, то A является полной решеткой.

Доказательство:

∆ Заметим, что если каждое подмножество точной нижней гранью обладает, следовательно, ей обладает и пустое множество, то есть в A существует наибольший элемент.

Требуется доказать, что A – полная решетка, то есть любое непустое подмножество имеет наибольший и наименьший элемент.

Рассмотрим X A, Y – множество всех верхних граней множества X в A и положим y = inf Y. Тогда любой элемент из X будет нижней гранью множества Y и, следовательно, x y для любого x X; если также x z для любого x X, то z Y и, следовательно, y z. Поэтому y = sup X. ▲

Определение 8. Упорядоченное множество (I, ) называется направленным, если для любых i, j I существует такой элемент k I, что i k, j k, то есть для любого двухэлементного множества из I существует верхняя граница.

Предложение 2. Пусть A – упорядоченное множество; тогда следующие три условия эквивалентны:

(i) Каждое непустое направленное подмножество множества A имеет точную верхнюю грань.

(ii) Каждая непустая цепь множества A имеет точную верхнюю грань.

Доказательство:

∆ Каждая вполне упорядоченная цепь является цепью, и каждая цепь направлена, следовательно, (i) (ii); чтобы закончить доказательство, покажем, что (ii) (i). Возьмем максимальную цепь, в ней существует точная верхняя грань. Тогда по лемме Цорна и направленное подмножество множества A имеет точную верхнюю грань.       ▲

Предложение 3 (лемма Цорна). Непустое упорядоченное множество, в котором каждая цепь обладает верхней гранью, имеет максимальный элемент, точнее для любого элемента a из A существует элемент b a, являющийся максимальным в A.

Лемма Цорна была предложена в 1935 году. Она часто заменяет рассуждения, основанные на таких эквивалентных ей принципах, как принцип максимальности Хаусдорфа, аксиома выбора, теорема Цермело о вполне упорядоченности.

Можно показать эквивалентность этих утверждений лемме Цорна, но мы не будем этого делать, так как это не является целью дипломной работы. Лемма Цорна принимается нами в качестве аксиомы.

 

Связь систем замыканий с операторами замыкания

 

В параграфе 1 были даны определения систем замыканий и операторов замыкания. Между ними существует взаимосвязь. Сформулируем эту взаимосвязь в качестве теоремы и докажем её.

Теорема 1. Каждая система замыканий D на множестве A определяет оператор замыкания  на A по правилу

(X) = ∩ { Y D | Y X }.

Обратно, каждый оператор замыкания  на A определяет систему замыканий

D = { X A | (X) = X }.

Доказательство:

∆ 1) Пусть дана система замыканий D и оператор , определенный по правилу (X) = ∩ { Y D | Y X }. Докажем, что  – оператор замыкания. Для этого проверим выполнимость условий J. 1 – J. 3. Этот оператор удовлетворяет условиям J. 1 – 2 по определению. По условию, D – система замыканий. Тогда

(X) = X X D,                                                    (1)

так как (X)  D, то отсюда вытекает J. 3.

2) Обратно, пусть задан оператор замыкания  (удовлетворяющий J. 1 – 3) и пусть

D = { X A | (X) = X }.                                           (2)

Докажем, что D – система замыканий. Если (X_i) _{i I} – произвольное семейство в D и ∩ X_i = X, то X X_i; следовательно, по J. 1. (X) (X_i) = X_i для всех i, и поэтому

(X) ∩ X_i = X.

Вместе с условием J. 2 это показывает, что (X) = X, то есть X D. Таким образом, с помощью  мы построили систему замыканий D.

3) Покажем, что соответствие D  взаимно однозначно.

Во-первых, пусть D – произвольная система замыканий,  – оператор, определенный равенством (X) = ∩{ Y D | Y X } для всех X A, и D ' – система замыканий, определенная оператором  по формуле (2). Тогда D ' = D в силу (1). Возьмем затем произвольный оператор замыкания , и пусть D – система замыканий, определенная оператором  по формуле (2), а  ' – оператор, определенный системой D по формуле (X) = ∩{ Y D | Y X }. Как только что было показано, D тогда также определяется оператором  ', и, следовательно,

(X) = X  ' (X) = X.                                           (3)

В силу J. 3, (X) = (X); поэтому из (3) вытекает, что  ' (X) = (X). Но X (X) и, применяя  ' получаем  ' (X)  ' (X) = (X), а обратное включение следует из соображений симметрии. ▲

Системы замыканий и операторы замыкания могут быть определены на любой полной решётке L и соотношения между ними, установленные в теореме 1, сохраняются.

На самом деле теорема 1 является частным случаем соответствующей теоремы (при L = B (A)) для произвольной полной решётки L.

Элементы системы D называются замкнутыми множествами множества A, а (X) называется замыканием множества X в A ((X) на самом деле замкнуто в силу J. 3). Как было отмечено, D является полной решеткой относительно . Точнее, если задано некоторое семейство (X_i) _{i I} в D, то множество ∩ X_i будет наибольшим замкнутым множеством, содержащимся во всех множествах X_i, а ∩{ Y D | Y X_i для всех i 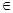I } – наименьшим замкнутым множеством, содержащим все множества X_i.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: