Алгебраические системы замыканий

 

Начнем с понятия алгебраической операции.

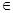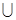Пусть A – универсальная алгебра с множеством алгебраических операций Ω. Каждая операция ω из Ω имеет определённую арность n, n N {0}.

Для любого натурального n n -арная операция ω – это отображение из Aⁿ в A, то есть каждой упорядоченной n -ке { a ₁; …; a_n } 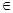Aⁿ операция ω ставит в соответствие однозначно определённый элемент ω(a ₁; …; a_n) из A.

В случае п = 1 это будет любое преобразование множества A (отображение A в себя).

Если n = 0, то a ⁰ – это одноэлементное множество и 0-арная операция ω переводит элемент a ⁰ в некоторый элемент ω(a ⁰) = ω из A, то есть 0-арная операция ω фиксирует некоторый элемент в A: является некоторым выделенным элементом алгебры A.

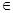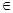Если дана универсальная алгебра A с множеством алгебраических операций Ω, то подмножество B A называется подалгеброй алгебры A, если оно замкнуто относительно всех операций из Ω. Иными словами, для любого ω Ω, n 1, и любых а ₁, а ₂, …, а_п B должно быть

ω(а ₁, а ₂, …, а_п) 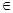B.

С другой стороны, элементы, отмечаемые в A всеми 0-арными операциями из Ω (если такие существуют), должны содержаться в подалгебре B.

Очевидно, что пересечение любой системы подалгебр универсальной алгебры A, если оно не пусто, будет подалгеброй этой алгебры.

Отсюда следует, что если X – непустое подмножество алгебры A, то в A существует наименьшая среди подалгебр, содержащих целиком множество X. То есть существует наименьшая подалгебра в A, содержащая X и она равна пересечению всех подалгебр алгебры A, содержащих X. Обозначим её через  и назовём подалгеброй, порожденной множеством X.

Стоит отметить, что пересечение подалгебр может быть пустым, если множество алгебраических операций Ω алгебры не содержит 0-арных операций.

Заметим, что система S (А) всех подалгебр алгебры A является алгебраической системой замыканий, то есть соответствующий оператор замыкания X  является алгебраическим.

Очевидно, что соответствие X  является оператором замыкания. Проверим, является ли он алгебраическим.

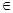
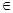Возьмём a , тогда a будет принадлежать и , где  – конечное подмножество множества X, так как элемент a получается путём применения конечного числа конечноместных n -арных операций ω Ω.

Справедливо и обратное утверждение:

Если D – произвольная алгебраическая система замыканий на множестве A, то для подходящего набора алгебраических операций Ω и соответствующей структуры   универсальной алгебры на A, имеем S (A) = D.

Для доказательства обозначим через (X) оператор замыкания для алгебраической системы замыканий D на множестве A. Зададим алгебраические операции на A следующим образом. Каждой n -ке a ₁, …, a_n 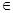A, где n 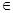N, и произвольному элементу b 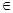({ a ₁, …, a_n }) поставим в соответствие свою n -арную операцию ω, определенную следующим правилом:

ω(x ₁, …, x_n) = 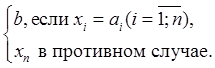              (4)

Это определяет структуру универсальной алгебры  на A, где для каждого натурального числа n операции из Ω заданы формулой (4). Таким образом определено бесконечно много алгебраических операций на множестве A, если A бесконечно.

Пусть _Ω(X) =  – оператор замыкания, соответствующий системе S (A) подалгебр универсальной алгебры A. Проверим, что (X) = _Ω(X).

Пусть X A и предположим сначала, что X конечно, то есть X = { c ₁, …, c_m }. Тогда (X) _Ω(X) по определению (4) алгебраических операций ω.

C другой стороны, так как (X) = (X), то для любой n -ки a ₁, …, a_n 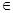(X) и для любой n -арной операции ω 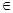Ω ω(a ₁, …, a_n) 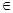({ a ₁, …, a_n }) (X) = (X). Поэтому (X) является подалгеброй алгебры  и, значит, _Ω(X) (X).

Пусть теперь X – произвольное подмножество множества A, тогда, так как оба оператора замыкания (X) и _Ω(X) – алгебраические (первый по предположению, а второй в силу доказанного выше), имеем

(X) = 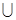(X ') = 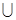_Ω(X ') = _Ω(X),

где X ' пробегает конечные подмножества множества X.

Итак, доказан следующий результат:

Теорема 2. Система S (A) подалгебр универсальной алгебры A является алгебраической системой замыканий. Обратно, если дана алгебраическая система замыканий D на множестве A, то для подходящего множества алгебраических операций Ω можно определить такую структуру универсальной алгебры на A, что S (A) = D.

Полученный выше результат можно использовать при построении оператора замыкания_Ω(X), соответствующего системе S (A) подалгебр универсальной алгебры A.

Отметим, что примеры 1 и 3 дают алгебраические системы замыканий, а система замкнутых множеств топологического пространства (пример 2), как правило, не алгебраическая.

Соответствия Галуа

 

Соответствия Галуа могут определятся разными взаимосвязями, имеющимися между различными понятиями. Нам будет наиболее интересен тот факт, что соответствия Галуа являются одним из наиболее важных примеров систем замыканий.

Для начала сформулируем понятие соответствия Галуа.

Пусть M и M ' упорядоченные множества, в которых отношение порядка обозначаются одинаково . И пусть указаны отображения
φ: M M ' и ψ: M ' M, удовлетворяющие (для любых a, b 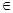M, a ', b ' 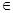M ') следующим требованиям:

a) если a b, то aφ bφ,

если a ' b ', то a ' ψ b ' ψ,

b) aφψ a, a ' ψφ a '.

Тогда пара (φ, ψ) называется соответствием Галуа между упорядоченными множествами M и M '.

Данное определение наиболее общее и формальное.

Рассмотрим теперь более конкретное задание соответствия Галуа, переобозначив отображения φ и ψ одинаково – символом ^*. Но при этом будем иметь в виду, что эти отображения всё-таки разные.

Пусть A и B – некоторые множества и Ф – соответствие из A в B, то есть подмножество прямого произведения A B. Для любого подмножества X множества A определим подмножество X ^* множества B равенством

X ^* = { y 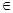B | (x, y) 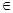Ф для всех 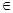x X }

и аналогично для любого подмножества Y множества B определим подмножество Y ^* множества A равенством

Y ^* = { x 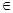A | (x, y) 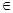Ф для всех y Y }.

Таким образом, имеем отображения

X X ^*, Y Y ^*                                                    (5)

множеств B (A), B (B) друг в друга, обладающие следующими свойствами:

если X ₁ X ₂, то   X ₁ ^* X ₂ ^*;                                                 (6)

если Y ₁ Y ₂, то Y ₁ ^* Y ₂ ^*;

X X ^**, Y Y ^**;                                                        (7)

X ^*** = X ^*, Y ^*** = Y ^*.                                                  (8)

Условия (6) и (7) вытекают непосредственно из определений; если (6) применить к (7), получаем X ^* X ^***, в то время как (7), примененное к X ^*, дает обратное неравенство. Таким образом, любые отображения (5), удовлетворяющие (6) и (7), удовлетворяют также (8).

Пара отображений (5) между булеанами B (A) и B (B) с отношением включения , или в более общем случае между любыми упорядоченными множествами, называется соответствием Галуа, если выполняются условия (6), (7) (и, следовательно, (8)).

Приведём наиболее интересные примеры соответствий Галуа.

Пример 4.1:   Пусть R – коммутативное кольцо с единицей. Определим соответствие в R правилом x y. Это соответствие устанавливает, в частности, соответствие Галуа между простыми идеалами кольца R и некоторыми мультипликативно замкнутыми подмножествами кольца R.

Идеал P кольца R назовём простым, если для 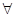a, b R: a ∙ b P a P или b P.

Возьмем простой идеал P кольца R. Поставим ему в соответствие множество P ^* = { y R: x y для всех x P } = R \ P – замкнутое относительно умножения.

Возьмем мультипликативно замкнутое подмножество Y. Поставим ему в соответствие множество Y ^* = { x R: x y для всех y Y} = R \Y – простой идеал.

Покажем выполнимость свойств.

Если P ₁ P ₂, то R \ P ₁ R \ P ₂ − очевидно, так как R \ P ₁ является дополнением к P ₁, а R \ P ₂ – дополнением к P ₂. Аналогично для Y ₁ Y ₂.

Возьмем подмножество P из множества простых идеалов R. Поставим ему в соответствие множество P ^* = R \ P, а P ^* поставим в соответствие P ^** = R \(R \ P) = P P P ^**.

Аналогично доказываются эти свойства для Y ₁ Y ₂.

Таким образом, построенное соответствие есть соответствие Галуа.

Пример 4.2:  В кольце A каждому его подмножеству X отвечает (левый) аннулятор, состоящий из тех элементов a A, для которых a ∙ x = 0 для каждого x из X:

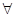Ann Х = { a A | x X a ∙ x = 0}.

Для подмножества X множества A определим подмножество X ^* множества A равенством

X ^* = { a A | a ∙ x = 0 для всех x X } = Ann Х

и аналогично для любого идеала I кольца A определим подмножество I ^* множества A равенством

I ^* = { x A | a ∙ x = 0 для всех a I } = Ann I.

Заметим, что в этом примере Ф = {(a, b) A ² | a ∙ b = 0}.

Таким образом, построены отображения X X ^* = Ann Х, I I ^* = Ann I. Проверим, является ли построенное соответствие соответствием Галуа.

1) Пусть X ₁ X ₂. Тогда X ₁ Ann Х ₁ = { a A | a ∙ x = 0 для всех x X ₁} и X ₂ Ann Х ₂ = { a A | a ∙ x = 0 для всех x X ₂}. Пусть a Ann Х ₂, a Х ₂ = 0, X ₁ X ₂ a Х ₁ = 0 a Ann Х ₁. Следовательно, Ann Х ₁ Ann Х ₂ или X ₁^* X ₂^*. Для I ₁ I ₂ аналогично получаем I ^*₁ I ^*₂.

2) Поставим множеству X в соответствие множество X ^* = Ann Х = I, а X ^* поставим в соответствие I ^* = Ann I = Ann (Ann Х). Если x Х, тогда a ∙ x = 0 для a Ann Х x Ann (Ann Х). Следовательно, X X ^**.

Аналогично получаем I I ^**, если поставить множеству I в соответствие множество I ^* = Ann I = X, а I ^* поставить в соответствие X ^* = Ann X = Ann (Ann I).

Таким образом, построенное соответствие есть соответствие Галуа.

Пример 4.3:   В группе G каждому подмножеству A соответствует централизатор C, который состоит из всех элементов c, коммутирующих с каждым элементом a из A:

C = { c G: для всех a A a · c = c · a }.

Пример 4.4:   В евклидовом пространстве V каждому подмножеству A множества V отвечает множество, состоящее из всех векторов, ортогональным векторам из A:

A  = { a A: для всех x V x a },

так что определена связь Галуа для подмножеств V. Здесь x a означает равенство 0 скалярного произведения (x, a).

Последние два примера обосновываются аналогично примеру 4.2.

Чтобы установить связь соответствий Галуа с системами замыканий, заметим, что при любом соответствии Галуа отображение X X ^** будет оператором замыкания в A, а Y Y ^** оператором замыкания в B (в силу (7) – (9)). При этом отображения X X ^*, Y Y ^* определяют взаимно однозначное соответствие между двумя этими системами замыканий.

Чтобы иметь более непосредственное описание алгебраических систем замыканий, нам необходимо еще одно определение.

Определение 8. Непустая система D подмножеств множества A называется индуктивной, если каждая цепь в D обладает точной верхней гранью в D.

В силу предложения 2 (примененного к B (A)) слово «цепь» здесь можно заменить словами «направленное множество».

Таким образом, мы получили следующую характеризацию алгебраических систем замыканий:

Теорема 3. Система замыканий является алгебраической тогда и только тогда, когда она индуктивна.

Доказательство:

∆ Пусть D − алгебраическая система замыканий на некотором множестве, K − цепь в D и K = sup K. Для доказательства включения K D нужно только проверить, что (H) K для каждого конечного подмножества H множества K. Пусть H = { x ₁, …, x_n }; тогда каждое x_i принадлежит некоторому члену цепи K, а так как K − цепь, то можно найти член L K, содержащий все x_i. Тогда H L K и L D; следовательно, (H) (L) = L K, то есть (H) K, что мы и хотели показать.

Обратно, пусть D – индуктивная система замыканий на A и  – соответствующий оператор замыкания. Нужно показать, что для любого X A

(X) = sup {(F) | F X, F конечно}.

Пусть K = {(F) | F X, F конечно} для фиксированного X A; тогда нужно показать, что sup K D. Отсюда будет следовать, что sup K = (X), поскольку sup K является наименьшим замкнутым множеством, содержащим все элементы множества X. Теперь для любых Y, Z A имеем

(Y) (Z) (Y Z),

и если Y, Z – конечные подмножества множества X, то Y 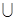Z также конечно. Это показывает, что K направлено, и, следовательно, sup K D, что и утверждалось.    ▲

Используя предложение 2, получаем

Следствие 1. Если D – алгебраическая система замыканий на A и K – направленная подсистема системы D, то sup K D.

Доказательство:

∆ Из леммы Цорна вытекает, что каждая непустая индуктивная система подмножеств множества A содержит максимальное подмножество.

Это приводит к следствию 2 из теоремы 2, в котором содержатся наиболее важные применения леммы Цорна к алгебре.

Следствие 2. Пусть D – алгебраическая система замыканий в A, и пусть A ₀, A ₁, B – такие подмножества множества A, что B D и B A ₁ = A ₀. Тогда D содержит элемент C, который является максимальным в D относительно свойств C B, C A ₁ = A ₀.

Доказательство:

∆ Для доказательства этого утверждения возьмём систему D ' всех таких множеств X D, что X B и X A ₁ = A ₀, и покажем, что D ' обладает максимальным элементом. Во-первых, D ' ≠ , так как B D '. Пусть теперь (X_i) – некоторая цепь в D ' и положим X = sup X_i. Тогда X D, так как система D индуктивна. Далее X B и X A ₁ = A ₀; поэтому X D '. Таким образом, система D ' индуктивна, и по лемме Цорна D ' обладает максимальным элементом.    ▲

 

Задачи

Задача 1. Установить, что при соответствии Галуа X X ^*, Y Y ^* выполняется тождество ( X_i)^* = X_i ^*, для произвольных семейств подмножеств (X_i) _{i I}.

Решение:

Без ограничения общности возьмём два множества X ₁ и X ₂ и покажем, что (X ₁ X ₂)^* = X ₁^* X ₂^*.

Множеству X ₁ поставим в соответствие множество X ₁^*:

X ₁^* = { y ₁ B |(x ₁, y ₁) Ф для всех x ₁ X ₁}.

Аналогично для множества X ₂:

X ₂^* = { y ₂ B |(x ₂, y ₂) Ф для всех x ₂ X ₂}.

Пусть X ₃ = X ₁ X ₂. Тогда (X ₁ X ₂)^* или X ₃^* будет иметь следующую структуру: X ₃^* = { y ₃ B |(x ₃, y ₃) Ф для всех x ₃ X ₃} или другими словами это такие y ₃ из B, что пары (x ₁, y ₃) и (x ₂, y ₃) должны принадлежать соответствию Ф одновременно для всех x ₁ и x ₂ из X ₁ X ₂. То есть множество элементов y ₃ из B это множество, состоящее из элементов y ₁ X ₁^* и y ₂ X ₂^*, которые одновременно должны удовлетворять соотношениям (x ₁, y ₁) Ф, (x ₁, y ₂) Ф, (x ₂, y ₁) Ф, (x ₂, y ₂) Ф. То есть элементы y ₃ принадлежат пересечению множеств X ₁^* и X ₂^*, что и требовалось показать.

Задача 2. Пусть X H (X) – произвольное отображение множества B (A) в себя. Показать, что (X) = H (X) X определяет оператор замыкания тогда и только тогда, когда X (Y) влечёт (X) (Y).

Решение:

a) докажем прямое утверждение: если (X) = H (X) X определяет оператор замыкания тогда X (Y) влечёт (X) (Y).

Пусть X (Y), то есть X H (Y) Y. Так как по условию (Y) = H (Y) Y – оператор замыкания, то для него выполняются аксиомы J. 1 – J. 3. Применим аксиому J. 1 к X H (Y) Y и аксиому J. 3 к ((Y)):

X H (Y) Y H (X) X H (H (Y) Y) (H (Y) Y) H (X) X H (Y) Y. То есть (X) (Y).

b) докажем обратное утверждение: если X (Y) влечёт (X) (Y) тогда (X) = H (X) X определяет оператор замыкания.

Для доказательства обратного утверждения, необходимо проверить выполнимость аксиом J. 1 – J. 3 оператора замыкания.

Для начала докажем вспомогательное утверждение о том, что Y X ^* тогда и только тогда, когда X Y ^*.

Доказательство:

∆ Докажем прямое утверждение.

Пусть Y X ^*. Тогда, применив к нему свойство (7), получим Y ^* X ^**. По свойству (7) имеем включение X X ^**. Следовательно, получаем X X ^** Y ^* или X Y ^*.

Докажем обратное утверждение.

Пусть X Y ^*. Тогда X ^* Y ^** Y   ▲

J. 1: пусть X Y и Y (X), тогда по доказанному выше утверждению включение Y (X) равносильным образом можно заменить на X (Y). Получим, что X X (Y) или X (Y). Тогда по условию пункта b) задачи X (Y) влечёт (X) (Y). Следовательно, если X Y, то (X) (Y).

J. 2: пусть X Y и Y (X) по утверждению, значит, X (X).

J. 3: по J. 2 X (X). Применим к нему свойство (7), получим (X) (X). Применим это же свойство к X (Y) (X) (Y), получим (X) (Y) (X) (Y). Далее по утверждению Y (X) (Y) (X). Получили (Y) (X) (Y). При этом (Y) (X) (по утверждению). Следовательно, мы получаем обратное включение (X) (X). Тем самым получили, что (X) = (X).

Следовательно, (X) = H (X) X – оператор замыкания.

Задача 3. Показать, что множество всех предупорядоченностей ρ на множестве A является алгебраической системой замыканий. Верно ли это для множества всех упорядоченностей?

Решение:

Непустое множество 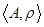 назовём предупорядоченным, если введенное на нём бинарное отношение ρ рефлексивно и транзитивно. Такое отношение ρ называется отношением предпорядка на A.

Пусть X A A, или X B (A A). Обозначим через J (X) пересечение всех предпорядков на A, содержащих X:

J (X) = { ρ – предпорядок на A: X ρ }.

Так как при пересечении бинарных отношений на множестве свойства рефлексивности и транзитивности сохраняются, то J (X) – наименьший предпорядок на A, содержащий X. Ясно, что A A является предпорядком на A. Поэтому система всех предпорядков на A является системой замыканий на этом множестве.

Остаётся проверить, будет ли система предпорядков алгебраической. Для этого возьмём произвольную пару (a, b) J (X), где X A A. Предпорядок J (X) получается из множества пар X добавлением пар вида (c, c), где c A, и его расширением по транзитивности: если уже получены пары (d, e) и (e, f), то добавляем и пару (d, f). При этом пара (a, b) в результате последовательного применения расширений по рефлексивности и транзитивности принадлежит конечному множеству пар F X. Следовательно, (a, b) J (F).

Для множества всех упорядоченностей верно лишь в том случае, когда множество A содержит один элемент. Иначе, не выполняется свойство антисимметричности.

Задача 4. Показать, что совокупность всех алгебраических систем замыканий на данном множестве A является системой замыканий на B (A). Всегда ли эта система замыканий будет алгебраической?

Решение:

Очевидно, что множество всех алгебраических систем замыкания на данном множестве A является системой замыкания на булеане B (A). Чтобы показать, является ли эта система алгебраической, воспользуемся теоремой 2.

Будем считать, что имеется семейство алгебр , i I. Каждой из них поставлена система подалгебр S (). Пересечению соответствующих систем замыканий соответствует алгебра 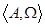, при Ω= . Для произвольного подмножества X в A рассмотрим подалгебру  алгебры