Группировка промышленных предприятий по численности рабочих за 19__г.

Группы предприятий по числу рабочих, чел	Число предприятий	Среднегодовая численность
	% к итогу	кумулятивные итоги	% к итогу	кумулятивные итоги
до 100	35,00	35,0	3,3	3,3
101-200	19,6	54,6	5,4	8,7
201-500	22,9	77,5	14,2	22,9
501-1000	11,3	88,8	15,3	38,2
1001-3000	8,4	97,2	26,8	65,0
3001-10000	2,5	99,7	23,6	88,6
10001 и более	0,3	100,0	11,4	100,0

 

РАЗДЕЛ 3. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ

 

3.1. Абсолютные величины

Абсолютной величиной называется статистический показатель, выражающий абсолютные размеры изучаемого явления.

По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные, которые отражают абсолютные размеры каждой отдельной единицы совокупности, и суммарные (групповые), которые получаются суммированием индивидуальных абсолютных величин.

Абсолютные величины - всегда числа именованные, имеющие определенную размерность, единицу измерения. В зависимости от различных причин и целей анализа применяют натуральные, условно-натуральные, трудовые и стоимостные единицы измерения.

Натуральные измерители в большинстве своем соответствуют природным или потребительским свойствам предмета изучения и выражаются в физических мерах веса, длины и т. д. Учет в натуральных единицах измерения называется натуральным учетом. Иногда применяется составная единица измерения (например, тоннокилометры - ткм и т. д.).

Однородная, но неодинаковая продукция измеряется в условно-натуральных единицах измерения. Такие единицы получают, приводя различные натуральные единицы к одной, принятой за базу, например, в консервной продукции емкость банки в 354,4 см³ принята за условную и вся продукция пересчитывается в этих условных банках. Аналогично производится пересчет в условно-натуральные измерители и в других отраслях (топливной, текстильной и пр.).

Показатели, отражающие результаты труда, измеряются в трудовых единицах измерения, а наиболее распространенные – в стоимостных (или денежных) единицах измерения.

3.2. Относительные величины: сущность, виды, единицы измерения

Статистические показатели, выражающие относительные размеры изучаемого явления, называются относительными величинами.

Относительные величины получаются в результате деления одной величины на другую, принимаемую за базу сравнения (или основание относительной величины). Причем следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучает, т.е. сравнимый показатель, а в знаменателе - показатель, с которым производится сравнение.

База сравнения выступает в качестве своеобразного измерителя. Если значение базы принимается за единицу (производится простое деление двух величин), то относительная величина выражается в коэффициенте (например, темпы роста), если основание (база) - 100%, то относительная величина выражается в процентах.

Иногда за базу принимают 1000 (при расчете коэффициентов рождаемости или смертности, естественного или механического прироста показателя, в фармации и т. д.). Такие единицы измерения называются промилле и обозначаются %₀.

Все относительные величины делятся на относительные величины выполнения плана и планового задания (в настоящее время лучше говорить о выполнении договорных обязательств), динамики, структуры, координации, интенсивности, сравнения, уровня экономического развития.

Относительная величина выполнения плана (ОВВП) - соотношение величины показателя, достигнутое за какое-то время или какому-либо моменту, и величины его, установленной по плану за это же время:

ОВВП = Факт(95)/План(95)

- факт (95) - фактическое выполнение за 1995 г.;

- план (95) - плановое значение за 1995 г.

Относительная величина планового задания (ОВПЗ) - соотношение плановой величины показателя к его фактически достигнутому уровню в предыдущем периоде (или в периоде, принятом за базу):

ОВПЗ = Факт(94)/План(95)

- факт (94) - фактическое выполнение за 1994 г.

Произведение этих двух величин дает относительную величину динамики (см. ниже): ОВД = ОВВП × ОВПЗ;

Относительная величина динамики (ОВД) - соотношение величины показателя за данное время и величины его за какое-либо аналогичное предшествующее время, принятое за базу сравнения. Относительная величина динамики характеризует степень, скорость изменения показателя во времени, в частности, темпы роста. Она выражается в виде краткого отношения (коэффициента) или в процентах. Если имеется ряд динамики (ряд во времени) абсолютных величин, то ОВД может исчисляться как отношение величины показателя за каждое последующее время к величине его за непосредственно предшествующее ему время или как отношение к величине его за одно и то же время, принятое за базу сравнения. В первом случае относительная величина динамики называется ОВД с переменной базой или цепная, во втором - с постоянной базой сравнения или базисная.

Если уровни ряда обозначить через Y _i , то ОВД вида:

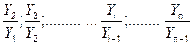называются цепными, а вида:

базисными (более подробно эта тема раскрывается в разделе рядов динамики).

Относительная величина структуры характеризует состав изучаемой совокупности и показывает какой удельный вес (какую долю) в общем итоге составляет каждая ее часть. Она получается в результате деления значения каждой части совокупности на их общий итог, принятой за базу.

Относительная величина координации характеризует соотношение отдельных частей целого, одна из которых принимается за базу сравнения и является дополнением к относительной величине структуры. Например, число сельских жителей, приходящихся на 100 городских и т. д.

Относительная величина интенсивности (степени) показывает степень распространенности данного явления в определенной среде. Обычно это отношение двух разноименных абсолютных величин (плотность населения на квадратный километр; производство сельскохозяйственной продукции на 1 га сельхозугодий и пр.).

Относительная величина сравнения характеризуют соотношение одноименных показателей, относящихся к различным объектам или территориям, но за один и тот же период времени.

Относительная величина уровня экономического развития – обычно соотношение величины важнейших экономических показателей (страны, региона, отрасли) и численности населения (так называемые показатели на душу населения).

 

Решение типовых задач

Задача 1. Мыловаренный завод произвел за отчетный период следующее количество продукции, т.:

мыло хозяйственное 40%-ное – 25,0; мыло туалетное – 20,0;

мыло хозяйственное 60%-ное – 22,0; порошок стиральный – 55,0.

Определите общий выпуск продукции в пересчете на условное 40%-ное мыло по следующим переводным коэффициентам: мыло 60%-ное и туалетное – 1,75, порошок стиральный – 0,5.

Решение. Перемножив фактический выпуск продукции на коэффициенты пересчета в условное 40%-ное мыло, получим:

25·1.0 + 22.0·1.75 + 20.0·1.75 + 55.0·0.5 =

= 126 тыс. т условного 40%-ного мыла.

Задача 2. По плану предусматривалось собрать по 30 ц пшеницы с гектара, а собрано по 33 ц. Определить выполнение плана по урожайности.

Решение. Поделим фактическую урожайность на плановую и получим:

(33 × 100)/30 = 110%

План по урожайности выполнен на 110%, или перевыполнен на 10%.

Задача 3. Планом предприятия предусматривалось повысить производительность труда на 5% и снизить затраты на 2%. Фактически производительность труда возросла на 6%, затраты были снижены на 4%. Определите выполнение плана по росту производительности труда и снижению затрат.

Решение. Степень выполнения плана по повышению производительности труда равна отношению достигнутого уровня - 106% (100% + 6%) к показателю плана - 105% (100% +5%) в процентах:

(106 × 100)/105 = 101%

Аналогично, фактическое снижение затрат - 96% (100% - 4%), а плановое - 98% (100% - 2%) их отношение дает 98%, т.е. план по снижению затрат перевыполнен на 2%.

Задача 4. Плановое задание по выпуску продукции на 1995 г. составило 04%, а выполнено на 105%. Определить относительную величину динамики.

Решение. Здесь 104% - это относительная величина планового задания, а 105%- это относительная величина выполнения плана, а так как ОВД = ОВВП × ОВПЗ, то (104 × 105)/100 = 109,2%, т.е. выпуск продукции в 1995 г. составил по сравнению с 1994 годом 109,2% или увеличился на 9,2%.

Задача 5. По данным переписи населения 1970 г. в СССР проживало в возрасте 100 лет и старше 19304 чел., из них мужчин - 4252 чел., женщин - 15052. Определите структуру долгожителей по полу и относительную величину координации, приняв число мужчин за базу, равную 100.

Решение. Для вычисления относительных величин структуры нужно разделить значение каждой части на общий итог, принимаемый за целое (100%). Количество мужчин и женщин в возрасте 100 лет и старше надо поделить на общее их число или исчислить удельный вес мужчин, а затем отнять его от 100%:

(4250 × 100)/19304 = 22% мужчин

женщин - 78% (100%-22%).

Относительные величины координации характеризуют соотношение отдельных частей совокупности. В задаче требуется вычислить соотношение между численностью мужчин и женщин в возрасте 100 лет и старше. Для этого, приняв число мужчин за базу сравнения, равную 100, поделим численность женщин на численность мужчин и получим

(15052 × 100)/4252 = 354

Это значит, что на каждые 100 мужчин в возрасте 100 лет и старше приходится 354 женщины в том же возрасте.

 

РАЗДЕЛ 4. СРЕДНИЕ ВЕЛИЧИНЫ

 

Средней величиной называется показатель, который дает обобщенную характеристику варьирующего признака единиц однородной совокупности.

Средняя отражает то общее, что скрывается в каждой единице совокупности, улавливает общие черты, общую тенденцию, закономерность, присущую данному распределению, она является равнодействующей, потому что в ней находит свое отражение, суммируется и синтезируется влияние всей совокупности факторов, под воздействием которых формируется ряд распределения. Средняя дает также характеристику центра распределения.

 

4.1. Средняя арифметическая

Обозначив индивидуальные значения признака через

x ₁, x ₂, x ₃, … …, x _n,

их количество - через n, можно записать:

Исчисленная таким образом средняя называется средней арифметической простой, т.е. она равна частному от деления суммы индивидуальных значений признака на их количество.

Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается один, или одинаковое количество раз, т. е. когда средняя рассчитывается по несгруппированным данным.

В том случае, когда мы имеем дискретный ряд распределения, т. е. когда значение признака встречается несколько раз, применяют среднюю арифметическую взвешенную, рассчитываемую по формуле:

Таблица 4.1

Заработная плата рабочих цеха за месяц, тыс. руб.

з/п (Х)
кол. (f)

По данным таблицы средняя заработная плата рассчитывается:

(100×2+200×5+300×20+400×30+500×15+600×10+700×5) / 87 = 36200 / 87 = 416 тыс.руб.

Таким образом, средняя арифметическая взвешенная равна сумме произведений индивидуальных значений признака x на их частоты или веса f, поделенной на сумму частот ∑ f.

Довольно часто в статистике приходится вычислять среднюю арифметическую в интервальном ряду, среднюю из групповых средних и среднюю из относительных величин.

При вычислении средней интервального ряда необходимо найти середину каждого интервала, и, взяв ее за значение признака использовать формулу средней арифметической взвешенной.

При вычислении средней из групповых (или частных) средних (например, при вычислении средней заработной платы по отрасли, когда имеется средняя заработная плата по предприятиям этой отрасли), в качестве индивидуальных значений признака берется соответствующая групповая средняя и рассчитывается по формуле средней арифметической взвешенной.

При вычислении средней из относительных величин в качестве весов (или частот) берут основание относительной величины, а в качестве значения признака - соответствующую этому основанию относительную величину.

 

Свойства средней арифметической

1) Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин.

2) Алгебраическая сумма отклонений индивидуальных значений признака от средней равно нулю.

3) Если все варианты ряда (значения признака) изменить на одно и то же число a или изменить в A раз, то и средняя изменится на a или в A раз соответственно.

4) Если все частоты ряда изменить в A раз, то средняя не изменится.

 

4.2. Средняя гармоническая

Во многих статистических исследованиях приходится сталкиваться с таким положением, когда известны значения индивидуального признака - x и произведения x×f, т.е. действительные значения весов (частот) неизвестны. В этом случае расчет средней производится с использованием среднейгармонической взвешенной, которая определяется по формуле:

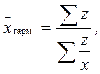
где Z=x×f, т.е. произведению значения признака на частоту.

В тех случаях, когда произведения x×f одинаковы или равны единице

x ₁∙ f ₁ = x ₂∙ f ₂ = … … = x_n ∙ f_n; x ₁∙ f ₁ = x ₂∙ f ₂ = … … = x_n ∙ f_n = 1,

применяется средняя гармоническая простая, определяемая по формуле:

где x - отдельные варианты (значения признака);

n - число наблюдений (общее число признаков или вариант).

Таким образом, средняя гармоническая представляет собой особый вид средней, которая применяется в тех случаях, когда известны варианты x и произведения вариантов на частоты - x×f, при отсутствии действительных весов.

4.3. Средняя геометрическая

В некоторых случаях приходится вычислять средний коэффициент роста в единицу времени. Коэффициент роста характеризует скорость изменения статистических показателей и представляет собой отношение величины показателя за два периода времени, как правило, за ряд смежных лет (табл. 4.2).

Таблица 4.2

Выпуск продукции предприятием за 1990 - 1993 гг. (у.д.е.)

Годы Показатели
Выпуск продукции, y	20.0	22.0	26.4	50.1
Коэффициент роста выпуска продукции по сравнению с предыдущим годом, к	-	22.0:20.0=1.1	26.4:22.0=1.2	50.1:26.4=1.9

 

Средняя, которая отражает средний коэффициент роста показателя за определенный период называется средней геометрической, которая равна корню степени m из произведений коэффициентов роста (m - число коэффициентов роста),

Средний коэффициент роста (среднюю геометрическую) можно определить и по значениям первого и последнего членов динамического ряда. Если первый уровень ряда обозначить , а последний - , то ,

где n - число членов ряда (число лет).

4.4. Средняя квадратическая

В тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Средние диаметры колес, труб, стволов, средние стороны квадратов и т.д. определяются при помощи средней квадратической.

Средняяквадратическая простая вычисляется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число: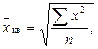

4.5. Соотношение между различными видами средних
(мажорантность средних)

Все выше рассмотренные виды средних величин можно получить из формулы степенной средней вида

При различных значениях показателя получаются различные средние, средняя арифметическая, гармоническая, геометрическая и квадратическая.

Мажорантность средних состоит в том, что средняя некоторого вида всегда больше средней некоторого другого вида (для признака, не могущего иметь отрицательных значений). В частности, если для одной совокупности вычислить средние гармоническую, геометрическую, арифметическую и квадратическую, то по численному значению они расположатся в возрастающем порядке. Порядок возрастания этих средних определяет показатель степени k в формуле степенной средней, т.е. чем больше k, тем больше средняя (табл.4.3).

Таблица 4.3

Порядок возрастания средних

k	-1
Название средней	гармоническая	геометрическая	арифметическая	квадратическая

Подробно общее условие мажорантности т.е. соотношения между различными видами средних было сформулировано А. Я. Боярским. Проиллюстрируем правило мажорантности геометрически (см. рисунок).

 

 

 

 

Соотношение между средней арифметической и средней геометрической двух чисел

 

Опишем на отрезке c = a + b, как на диаметре, полукруг и восстановим из общей точки отрезка a и b перпендикуляр, длина которого будет равна. . Восстановим также перпендикуляр из центра полукруга, длина которого будет равна (a + b)/2.

Из рисунка видно, что средняя геометрическая меньше средней арифметической. При этом, чем меньше отличаются отрезки а и b друг от друга, тем меньше разница между средними.

 

4.6. Мода и медиана

Кроме средних в статистике для описательной характеристики величины варьирующего признака пользуются показателями моды и медианы.

Мода - это наиболее часто встречающийся вариант ряда. Мода применяется, например при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар и пр.

Модой в дискретном ряду называется варианта (значение признака), имеющая наибольшую частоту (повторяющаяся самое большое количество раз), например: имеем данные о продаже магазином обуви по размерам (табл.4.4):

Таблица 4.4

Размер обуви x								Итого
Число пар f
Накопленная частота

 

В этом примере модой является 35-й размер, так как обуви такого размера продано больше всего - 187 пар.

Если мы имеем интервальный ряд, то для определения моды необходимо сначала определить модальный интервал, причем, если интервалы равны, то модальный интервал определяется по наибольшей частоте, а если неравны, то по наибольшей плотности. При равных интервалах мода внутри модального интервала может определяться по формуле:

Мо

где x ₀ - нижняя граница модального интервала;

h - величина (ширина) интервала; f _m - частота модального интервала;

f_{m -1} - частота интервала, предшествующего модальному;

f _m+1 - частота интервала, следующего за модальным.

Мода является наиболее распространенной и в этом смысле типичной величиной в распределении. Но мода и средняя величина по разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Поэтому мода по своему обобщающему значению уступает средней, которая характеризует совокупность в целом, так как складывается под воздействием всех без исключения элементов совокупности.

При наличии одной моды распределение называют унимодальным, при двух модах - бимодальным, при трех и более модах - мультимодальным.

Медианой называется варианта, которая приходится на середину ряда, расположенного в порядке возрастания или убывания численных значений признака. Медиана делит ряд на две равные части.

Если в совокупности нечетное число единиц, т. е. 2 m +1, то значение признака у (m +1)-ой единицы будет медианным. Если в совокупности четное число, т.е. 2∙ m единиц, то медиана равна средней арифметической из двух серединных значений вариантов.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот, а затем определяют, какое значение признака приходится на нее. В примере с размером обуви (см. табл.4.4) медианой является 35-й размер, так как именно он приходится на полусумму частот (500:2=250). Это значит, что 35-й размер делит ряд на две равные части.

При вычислении медианы для интервального вариационного ряда вначале определяют медианный интервал, т.е. первый интервал, накопленная частота которого принимает полусумму частот, а затем приближенное значение медианы по формуле:

Ме

где f_m - сумма частот;

x ₀ - нижняя граница медианного интервала; h - ширина интервала;

S_{m -1} - сумма накопленных частот интервалов, предшествующих медианному;

f_m - частота медианного интервала.

Главное свойство медианы состоит в том, что сумма абсолютных отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):

∑| x -Ме| = min.

Медиану, являющуюся описательной характеристикой вариационного ряда, иногда называют непараметрической средней. Медиана меньше, чем средняя арифметическая, зависит от формы распределения признака. Она не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда. Вот почему в медиане не находят отражения важные свойства совокупности и она используется обычно для решения некоторых частных задач, связанных с определением оптимума, совпадающего с вариантой, приходящейся на середину ряда.

Мода и медиана являются описательными характеристиками совокупностей с количественно варьирующими признаками и не могут заменить среднюю обобщающую величину. Величина моды и медианы, как правило, отличается от величины средней, совпадая с ней только в случае симметрии вариационного ряда.

 

Решение типовых задач

Задача 1. По следующим данным определите средний стаж рабочего (табл.4.5):

Таблица 4.5

Общий стаж работы, лет	до 5	5-10	10-15	15-20	20-25	25 и более	Итого
Число рабочих

Решение. Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения - интервальный, причем первый и последний интервал - открытые.

Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала

.

Задача 2. Все частоты уменьшились в два раза, а все варианты увеличились на две единицы. Что произойдет со средней?

Решение. Согласно свойствам средней арифметической, если все частоты ряда уменьшить или увеличить в одинаковое количество раз, то средняя не изменится, т.е. с точки зрения частот - средняя не изменится. Если все варианты увеличить или уменьшить на одно и то же число, то и средняя изменится на это же число. В нашем случае средняя увеличится на две единицы.

Задача 3. Двое рабочих в течение 8-часового рабочего дня изготовляют одни и те же детали. Первый из них тратит на изготовление детали 30 мин., второй - 40 мин. Вычислите среднюю затрату времени на изготовление одной детали.

Решение. В этой задаче явно даны только значения признака - затраты времени, а частоты, которыми является количество изготовленных каждым рабочим деталей, в явном виде не присутствуют. Однако произведения значений признака на частоты дает количество проработанного времени - 8 час. Так как произведения признака на частоту равны, то средняя определяется по формуле средней гармонической простой:

мин.

Задача 4. Автомобиль проехал 1000 км, из них 480 км он прошел со скоростью 60 км/час, 320 - со скоростью 80 км/час и 200 км - со скоростью 50 км/час. Определите среднюю скорость, с которой совершался рейс.

Решение. В этой задаче опять известны только значения признака, а значения частот (время) не даны, однако имеются данные о пройденном расстоянии, которое является произведением признака на частоту. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:

км/ч.

Задача 5. Определите среднегодовой темп роста выпуска продукции на заводе, если в 1990 г. было произведено продукции на 21,15 у.д.е., а в 1995 г. было запланировано произвести продукции на 35 у.д.е.

Решение. Для определения средних темпов роста применяется средняя геометрическая. Когда имеются данные о первом периоде (в нашем случае - выпуск продукции в 1990 г. на сумму 21,15 у.д.е.) и в последнем периоде (в задаче — выпуск продукции по плану в 1995 г. на сумму 35 у.д.е.), среднегодовой темп роста определяется по формуле:

Задача 6. Определить моду и медиану по следующим данным (табл. 4.6):

Таблица 4.6

Распределение студентов заочного отделения по возрасту

Возрастные группы	Число студентов	Накопленные частоты
до 20 лет
20-25
25-30
30-35
35-40
40-45
45 лет и выше
Итого:

 

Решение. Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда

Мо лет.

Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 25-30, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (3462: 2=1731). Тогда медиана определится как:

Ме года.

 

РАЗДЕЛ 5. ПОКАЗАТЕЛИ ВАРИАЦИИ И ДРУГИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ

5.1. Понятие о вариации

При изучении процессов и явлений общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующей отдельные единицы совокупности. Величина признака изменяется, колеблется под влиянием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.

Таблица 5.1

Дневная выработка рабочих двух бригад

Номер бригады	Число рабочих	Дневная выработка деталей отдельных рабочих, шт.	Средняя дневная выработка
		75 90 78 82 93 86
		65 122 84 70 105 58

Одна и та же средняя может характеризовать совокупность, в которой размеры вариации признака существенно отличаются друг от друга (табл.5.1). Как видно, средняя дневная выработка в обеих бригадах одинакова, хотя в первой бригаде средняя значительно меньше отличается от индивидуальных значений признака, чем во второй.

Следовательно, для всесторонней характеристики рядов распределения необходимы показатели, определяющие меру, степень колеблемости отдельных значений признака от средней, т.е. степень вариации, а также форму (тип) распределения, характеризующую ее закономерности.

5.2. Показатели вариации и способы их расчета

а) Размах вариации является наиболее простой мерой колеблемости значений признака и представляет собой разность между максимальным и минимальным значением признака: R = Х _max - Х _min.

Размах вариации имеет недостаток, проявляющийся в том, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость признака.

В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней.

Такими показателями являются среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

б) Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений индивидуальных значений признаков от их средней:

; .

Недостаток среднего линейного отклонения в том, что оно берется без учета знака. Поэтому в статистике чаще используют дисперсию и среднее квадратическое отклонение.

в) Дисперсия и среднее квадратическое отклонение. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины

; .

Дисперсия имеет очень большое значение в анализе. Однако ее применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому вычисляют среднее квадратическое отклонение, равное корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии

.

Сопоставление линейных или средних квадратических отклонений по нескольким совокупностям дает возможность определять степень их однородности в отношении того или иного признака. Чем меньше: R, d, σ²,σ, тем совокупность более однородна, тем более типичной будет средняя величина.

г) Коэффициент вариации. Так как дисперсия и среднее квадратическое отклонение характеризуют абсолютный размер отклонений, то представляет интерес сопоставить среднее квадратическое отклонение с его средней величиной. Такой показатель называется коэффициентом вариации

.

Если взять отношение среднего линейного отклонения к средней арифметической, то получим линейный коэффициент вариации .

Отношение размаха вариации к средней арифметической называется коэффициентом осцилляции: .

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: