Взаимосвязь показателей вариации

В нормальном ряду распределения между показателями вариации имеются следующие примерные соотношения:

5.3. Основные свойства дисперсии

1. Если все значения признака уменьшить или увеличить на какое-то постоянное число а, то дисперсия не изменится.

2. Если все значения признака уменьшить или увеличить в К раз, то дисперсия изменится в К ² раз.

3. Сумма квадратов отклонений индивидуальных значений признака x от их средней меньше суммы квадратов отклонений индивидуальных значений признака от любого числа а, при условии, что

.

4. Дисперсия признака равна разности между средним квадратом значения признака и квадратом их средней:

.

Дисперсия альтернативного признака

В ряде случаев возникает необходимость измерить вариацию альтернативного признака, то есть такого, который может принимать только два значения. Обозначив отсутствие интересующего нас признака через 0, его наличие через 1, долю единиц, обладающих данным признаком - через р, не обладающих — через q, дисперсию этого признака можно определить как

Например, если 64% работников предприятия имеют высшее образование р, то дисперсия будет равна:

.

5.4. Правило сложения дисперсий

На вариацию признака влияют различные причины и факторы, которые делятся на случайные и систематические. Поэтому и вариация может быть случайной, вызванной действием случайных причин и систематической, обусловленной воздействием постоянных причин и факторов. В связи с этим возникает необходимость в определении случайной систематической составляющей и её роли в общей вариации. Общую дисперсию мы уже рассматривали. Она характеризует общую вариацию признака под влиянием всех условий, всех причин, вызывающих эту вариацию и исчисляется по формуле:

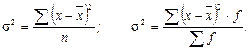
Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой. Вариация, обусловленная фактором, положенным в основание группировки, называется межгрупповой вариацией. Размеры ее определяются при помощи дисперсии групповых средних или межгрупповой дисперсии, которая характеризует колеблемость групповых или частных средних около их общей средней:

,

где - средняя по каждой отдельной группе; - средняя по всей совокупности; n - число единиц совокупности; f - частоты или веса.

Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней. Она характеризует систематическую вариацию, которая возникает под влиянием фактора, признака, положенного в основание группировки.

Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем и среднюю из внутригрупповых дисперсий:

где x - индивидуальные значения признака; - групповые или частные средние:

В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.

Это правило называется правилом сложения дисперсий.

5.5. Ряды распределения и их моделирование

а) Моменты распределения

Одной из важных задач анализов рядов распределения является выявление закономерности распределения, определение ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.

Кроме рассмотренных выше важной характеристикой рядов распределения являются моменты распределения.

Моментом распределения (М _к) называется средняя арифметическая из отклонений значений признака x от некоторой постоянной величины а в степени к:

Величина к определяет порядок момента. В зависимости от величины а различают начальные, центральные и условные моменты (табл. 5.2).

 

Таблица 5.2

Значение моментов распределения

Величина	Название момента	Обозначение момента	Величина момента
			к =0	к =1	к =2
	начальный	М
	центральный	M			σ
а	условный	М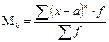

 

Условные моменты используются для определения дисперсий высоких степеней. Практически используются моменты первых четырех порядков. Если в качестве весов взять не частоты, а вероятности, то получим теоретические моменты распределения.

б) Кривые распределения

Для обобщенной характеристики особенностей формы распределения применяются кривые распределения, которые выражают закономерность распределения единиц совокупности по величине варьирующего признака.

Эмпирическая кривая - это фактическая кривая, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение (кривая 1, рис.5.3)

Теоретическая кривая распределения - это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения (кривая 2, рис.5.3).

По форме кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута, различаютправостороннюю асимметрию илевостороннюю асимметрию (рис.5.1). Кривые распределения также могут иметь различную островершинность (рис.5.2).

Для характеристики степени асимметрии кривой используют коэффициент асимметрии, который представляет собой отношение центрального момента третьего порядка к среднему квадратическому отклонению в кубе

.

Если А > 0, то асимметрия правосторонняя, а если А < 0, то асимметрия левосторонняя, в симметричном распределении - А = 0. Кроме этого коэффициента для характеристики асимметрии применяют и соотношение между и модой или медианой по отношению к среднеквадратическому отклонению.

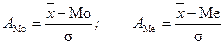. Он менее точен по сравнению с коэффициентом асимметрии и применяется реже.

Для характеристики островершинности кривой распределения применяют коэффициент эксцесса, который равен отношению центрального момента четвертого порядка к дисперсии в квадрате

.

В нормальном распределении Е =3, поэтому, если Е >3, то эксцесс выше нормального (островершинная кривая), Е <3, эксцесс ниже нормального (плосковершинная кривая).

в) Моделирование рядов распределения

Все рассмотренные выше показатели характеризуют отдельные свойства совокупности. Общую характеристику ряда распределения можно представить аналитически, в виде функции, характеризующей зависимость между изменениями признака и частотами. Если имеется эмпирический ряд распределения, то необходимо найти функцию распределения, т. е. подобрать такую теоретическую кривую, которая наиболее полно бы раскрывала закономерность распределения. Нахождение функции кривой распределения называется моделированием.

Для аппроксимации (выравнивания) эмпирических кривых распределения в статистике часто пользуются нормальным распределением, функция которого ,

где F (x) - интегральная функция распределения; t - нормированное отклонение; e - основание натуральных логарифмов.

Теоретическое распределение вероятностей и частот дает представление о форме, типе распределения, о закономерности, свойственной изучаемому явлению.

>Ме>Мо =Ме=Мо <Ме<Мо

Правосторонняя Симметричная Левосторонняя

Асимметрия кривая асимметрия

Рис.5.1. Типы кривых распределения (по асимметрии)

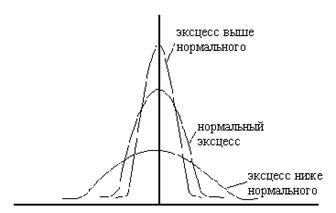Рис. 5.2. Типы кривых распределения (по островершинности)

Эмпирическое и теоретическое распределение рабочих по степени выполнения норм приведено в табл.5.3 и на рис.5.3.

Таблица 5.3

Распределение рабочих по степени выполнения норм выработки

Группы рабочих по степени выполнения норм,%	Число рабочих (эмпирические частоты) (f)	Теоретические частоты (f’)
до 100
100-110
110-120
120-130
130-140
140-150
150 и выше
Итого:

г) критерии согласия

Для оценки близости эмпирического и теоретического распределения используются специальные показатели, которые называются критериями согласия. Критерии согласия как правило тем или иным способом оценивают степень расхождения между эмпирическими и теоретическими частотами.

Наиболее часто используется критерий, который называется хи-квадрат Пирсона и рассчитывается ,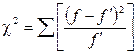

где f’ -теоретические частоты, f -эмпирические частоты.

Чем меньше значение , тем лучше теоретическое распределение отражает реальное положение в совокупности и наоборот. Если =0, то расхождение между f и f’ отсутствует.

Для проверки согласия с помощью рассчитанное значение сравнивают с табличным и при условии < можно с определенной вероятностью сказать, что расхождение теоретического и эмпирического распределения случайно, и наоборот.

Также применяется и критерий согласия Колмогорова , который равен , где D - максимальная разность накопленных частот (без учета знака), n - объем совокупности.

Вычислив фактический критерий , по специальной таблице находят вероятность достижения критерием этого значения. Если вероятность значительна, то расхождение между эмпирическим и теоретическим распределением можно считать случайным.

В явлениях общественной жизни асимметричные распределения встречаются гораздо чаще, чем симметричные. Некоторые асимметричные распределения могут быть приведены к симметричному путем преобразования признака Х, например логарифмированием. В этом случае распределение называется логарифмически нормальным. Такое преобразование производится, как правило, для сильно асимметричных распределений.

 

Решение типовых задач

Задача 1. Проверка пряжи на крепость в лаборатории дала следующие результаты (табл. 5.4):

Таблица 5.4

Крепость пряжи, г (х)
Количество проб, (f)

Вычислить все показатели вариации.

Решение. В задаче значения признака имеют различную численность, поэтому значения, , d, , , V должны вычисляться как средние взвешенные величины. Для вычисления показателей вариации проводим дополнительные расчеты (табл. 5.5)

Таблица 5.5

x	f	xf	(x - )	(x - ) f	(x - )2	(x - )2 f
			-29	-58
			-19	-247
			-9	-216
Итого				+521 -521

 

Средняя крепость пряжи определяется по формуле

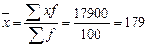г.

Размах вариации

г.

Среднее линейное отклонение вычисляется по формуле

г.

Дисперсия, взвешенная по частоте вариантов, равна

г².

Среднее квадратичное отклонение равно:

г.

коэффициент вариации составляет

.

Задача 2. На предприятии 64% работников имеют среднее и высшее образование. Определить дисперсию доли рабочих, имеющих среднее и высшее образование.

Решение. Дисперсия альтернативного признака определяется как = pq,где p – доля единиц совокупности, обладающих данным признаком, а q =1- p – доля единиц совокупности, не обладающих данным признаком, следовательно: =0,64·0,36=0,2304.

Задача 3. Имеются следующие данные (табл.5.6):

Таблица 5.6

Заработная плата рабочих по профессиям (1997 год), тыс. руб.

№ п/п	Группы рабочих по профессиям	Число рабочих	З/п одного рабочего в месяц
	Токари		140, 160
	Слесари		120, 200, 160
	Кузнецы		140, 180, 200, 220, 260

Вычислить:

среднюю месячную заработную плату для каждой группы и для всех рабочих; групповые дисперсии; среднюю из внутригрупповых дисперсий; межгрупповую дисперсию; общую дисперсию; проверить правило сложения дисперсий и сделать выводы.

Решение. В задаче требуется определить, как влияют на изменение заработной платы рабочих постоянные причины, положенные в основание группировки (в данном случае - различия в профессии), и случайные причины. Для этого необходимо определить систематическую и случайную вариации и их роль в общей вариации. Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу (табл.5.7).

Таблица 5.7

№ п/п	x	x –
Токари
		-10		-38
				-18
Итого:
Слесари
		-40		-58
				-18
Итого:
Кузнецы
		-60		-38
		-20
Итого:
Всего:

Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:

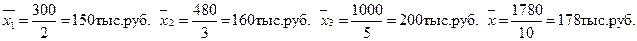
Внутригрупповые дисперсии вычисляем по формуле:

Средняя из внутригрупповых дисперсий равна:

Межгрупповая дисперсия определяется как:

,

Общая дисперсия равна:

По правилу сложения дисперсий общая дисперсия равна сумме средней внутригрупповых и межгрупповой дисперсии: s² = ² + d² = 1140 + 496 = 1636.

 

Задача 4. Средняя успеваемость студентов экономического факультета =4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).

Решение. В симметричном распределении =Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как <Ме<Мо, то разности между –Ме и –Мо отрицательные и асимметрия левосторонняя.

Задача 5. Урожайность сахарной свеклы в сельхозпредприятиях области характеризуется следующими показателями: =300 ц/га, =120 ц/га, Мо=240 ц/га, а урожайность зерновых - =30ц/га; =10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?

Решение.

Асимметрия правосторонняя, так как >0, и больше в первом случае.

Задача 6. Центральный момент третьего порядка =34,56 при =12. Вычислить коэффициент асимметрии и сделать выводы; центральный момент четвертого порядка =64,32 при =2. Вычислить коэффициент эксцесса и сделать выводы.

Решение.

Асимметрия правосторонняя, так как A>0, и незначительная

Эксцесс выше нормального, потому что E>3.

 

 

РАЗДЕЛ 6. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

6.1. Общие сведения о выборочном наблюдении

В связи с тем, что статистика имеет дело с массовыми совокупностями статистические исследования весьма трудоемки. Поэтому давно возникла мысль о замене сплошного наблюдения выборочным.

Выборочное наблюдение - это наиболее совершенный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь ее часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.

При проведении выборочного наблюдения нельзя получить абсолютно точные данные. Как при сплошном, так как при выборочном наблюдении неизбежны ошибки, которые делятся на ошибки регистрации и ошибки репрезентативности. В свою очередь, ошибки репрезентативности бывают случайные и систематические.

Важнейшим условием применения выборочного метода является правильный отбор единиц совокупности, а именно:

а) строго объективный отбор единиц совокупности, при котором каждая из них получала бы абсолютно одинаковую возможность попасть в выборку;

б) достаточное количество отобранных единиц совокупности. При соблюдении этих условий выборка будет репрезентативной или представительной.

Вся совокупность единиц, из которой производится отбор, называется генеральной совокупностью и обозначается буквой N. Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью и обозначается n.

Обобщающие показатели генеральной совокупности - средняя, дисперсная и доля - называются генеральными и соответственно обозначается σ, р, где p - доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численности генеральной совокупности, т.е. . Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно , ², ω.

Теоретической основой выборочного метода является теорема П.Л.Чебышева, которая формулируется следующим образом: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала:

< ε.

При практическом использовании теоремы Чебышева генеральную дисперсию , которая неизвестна, заменяют выборочной дисперсией.

 

6.2. Виды и схемы отбора

Формирование выборочной совокупности из генеральной может осуществляться по-разному. Различают следующие виды отбора: собственно-случайный; механический; типический; серийный; комбинированный.

5. Собственно-случайный отбор. Он ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. Либо применяется жеребьевка, либо используются таблицы случайных чисел.

6. Механический отбор. Он состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы), причем все единицы генеральной совокупности должны располагаться в определенном порядке. Размер интервала или группы равен обратной величине доли выборки (или количеству отбираемых единиц). Из каждой группы (интервала) берется только одна единица. Так, при 2%-ной выборке отбирается каждая 50-ая единица (1:0,02; или формируется 50 групп или интервалов), при 20%-ной выборке - каждая 5-я единица (1:0,2) и т. д.

7. Типический отбор. При его осуществлении вся генеральная совокупность делится на группы по типическому признаку, а затем в каждой группе проводится тот или иной отбор. Наиболее часто из каждой группы выбирается количество единиц, пропорциональное удельному весу группы в общей совокупности и как правило - механическим отбором. Такой отбор часто называют пропорциональным типическим отбором с механической выборкой.

8. Серийный отбор с равновеликими сериями состоит в выборке не отдельных единиц генеральной совокупности, а целых серий (гнезд). Попавшие в выборку серии подвергаются сплошному наблюдению. Сами серии могут формироваться различными методами и способами.

9. Комбинированный отбор. Все вышеперечисленные виды отбора комбинируются между собой.

Используя различные виды отбора, можно применить и различные схемы отбора: бесповторный отбор (схема невозвращенного шара)- после выбора какой-либо единицы она обратно в генеральную совокупность не попадает и не может быть выбрана снова; повторный отбор (схема возвращенного шара) - после выбора какой-либо единицы она вновь возвращается в генеральную совокупность и может быть выбрана снова.

 

6.3. Определение средних и предельных ошибок при

различных видах отбора

Ошибка выборки - разность между характеристиками выборочной и генеральной совокупности.

Если 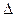представляет собой предел, которого не превосходит абсолютная величина то

Ошибка выборки зависит от многих факторов, и, если из одной и той же генеральной совокупности можно сформировать бесконечное множество выборочных совокупностей, каждая из них даст и свою ошибку. Поэтому при выборочном наблюдении говорят о средней из возможных ошибок ( средняя или стандартная ошибка выборки), которую обозначают как .

Величина 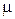прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности;

, для доли, соответственно .

Эти формулы справедливы для повторной схемы отбора. При бесповторном отборе вводится поправочный коэффициент, равный

, тогда .

В тех случаях, когда выборка небольшая этим множителем можно пренебречь, так как его значение близко к единице (обычно при ).

Для решения практических задач важна не средняя ошибка выборки, а пределы, за которые она не выйдет, т.е. говорят о предельной ошибке выборки.

Предельная ошибка выборки связана со средней ошибкой соотношением , где t - коэффициент доверия, или t - статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t =1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t =2 - P =0,954 или 95,4%; t =3 - P =0,997 или 99,7%.

Таким образом, предельная ошибка выборки зависит от трех факторов: дисперсии , объема выборки n, и коэффициента доверия t. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6.1.

Таблица 6.1

Определение предельной ошибки выборки при различных видах отбора

	Схема отбора	Предельная ошибка выборки
	для средней	для доли
Собственно - случайный и механический отбор
Повторный отбор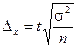
Бесповторный отбор
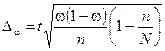
Типический отбор
Поторный отбор
Бесповторный отбор
Серийный отбор
Повторный отбор
Бесповторный отбор

 

6.4. Определение необходимой численности выборки

При разработке выборочного наблюдения предполагают заранее заданными величину допустимой ошибки выборки и вероятность ответа (и t). Неизвестным, следовательно, остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Из формулы и формул предельных ошибок выборки устанавливаем необходимую численность выборки. Формулы для определения численности выборки n зависят от способа отбора (табл.6.2).

Таблица 6.2

Формулы расчета численности выборки при собственно-случайном отборе

Способ отбора	Для средней	Для доли	Для доли, если даже приблизительно она неизвестна
Повторный
Бесповторный

Численность выборки можно выразить через отношение , т.е. предельную ошибку выборки выражают в единицах среднего квадратичного отклонения. Так, например, формула численности бесповторной собственно-случайной выборки для средней при t =3 примет вид .

Для типического и серийного отбора объем выборки определяется по специальным формулам.

Решение типовых задач

Задача 1. Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате был установлен средний вес детали - 30 г при среднеквадратическом отклонении равном 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес детали в генеральной совокупности.

Решение.

Предельная ошибка средней при собственно-случайном отборе (повторная выборка) определится по формуле

.

Нам известно, что t =2 (т.к. P =0.954); ; n =200, тогда

.

Следовательно, с вероятностью 0,954 можно утверждать, что средний вес детали в генеральной совокупности будет находиться в пределах

.

Задача 2. Был проведен учет городского населения города А методом случайного бесповторного отбора. Из общей численности населения 500 тыс. человек было отобрано 500 тыс. и установлено, что 15% имеют возраст старше 60 лет. С вероятностью 0,683 определить предел, в котором находится доля жителей города А в возрасте старше 60 лет.

Решение.

Предельная ошибка доли при собственно-случайном бесповторном отборе определится как

.

Здесь 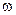=0.15; 1- 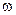= ; n =50; N =500; t =1 (P =0.683), тогда подставляя эти данные в формулу получим:

Следовательно, с вероятностью 0,683 можно утверждать, что доля жителей старше 60 лет находится в пределах:

0,15-0,048< P <0,15+0,048; или 10,2%< P <19,8%.

Задача 3. Проведена 10%-ная типическая выборка пропорциональна численности отобранных групп (табл. 6.3).

Таблица 6.3

Группировка рабочих разных профессий по степени выполнения

норм выработки

Группы рабочих	Число рабочих	Среднее выполнение норм, %
Токари
Слесари
Фрезеровщики

 

Требуется с вероятностью 0,954 определить пределы, в которых находится средний процент выполнения норм рабочими завода в целом. Выборка бесповторная.

Решение: Вычислим общий средний процент выполнения норм выработки:

.

Далее определим среднюю из групповых дисперсий

.

Рассчитаем предельную ошибку выработки для типического отбора

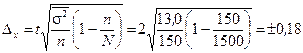. (N =1500, т.к. выборка 10%-ная).

Таким образом, с вероятностью 0,954 можно утверждать, что средний процент выполнения норм рабочими завода в целом находится в пределах

или

т.е. он не меньше 103,82% и не больше 104,18%.

Задача 4. Для определения средней урожайности сахарной свеклы в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25. Средняя урожайность по каждому отобранному району составила: 250, 260, 275, 280, 300 ц/га. Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность сахарной свеклы по области.

Решение. Найдем общую среднюю

ц/га.

Определим межсерийную дисперсию по формуле

ц/га.

Рассчитаем предельную ошибку выборки при серийном бесповторном отборе

ц/га.

Следовательно, с вероятностью 0,954 можно утверждать, что средняя урожайность сахарной свеклы в области будет находиться в пределах от 272,66 до 287,34 ц/га.

Задача 5. Предполагается, что партия деталей содержит 8 % брака. Определить необходимый объем выборки, чтобы с вероятностью 0,954 можно было установить долю брака с погрешностью не более 2%. Исследуемая партия содержит 5000 деталей.

Решение. По условию задачи t =2, доля бракованных деталей