 |
Матричные игры. Равновесная ситуация.
|
|
|
|
РАЗДЕЛ 2. ИГРОВЫЕ МЕТОДЫ
Глава 4. Матричные игры
Предмет и задачи теории игр.
Матричные игры. Равновесная ситуация.
Смешанные стратегии матричных игр.
Игры с природой.
Глава 5. Биматричные игры.
Игры с ненулевой суммой.
Борьба за рынки.
Дилемма узников.
Кооперативные игры.
Принятие решений в условиях неопределенности или частичной неопределенности.
Глава 4. Матричные игры
Предмет и задачи теории игр.
В экономике часто сталкиваются с ситуациями, когда эффективность решений одних участников экономического процесса зависит от решений, принятых другими участниками. При этом каждое предприятие сознательно стремится добиться наилучших результатов за счет других. Такие ситуации называются конфликтными. При этом ни одна из сторон не может полностью контролировать положение, так как все участники процесса принимают решения в условиях неопределенности.
Построением математических моделей конфликтных ситуаций и разработкой методов решения возникающих в этих ситуациях задач занимается теория игр.
Методы и рекомендации теории игр применимы к однократно повторяющимся конфликтным ситуациям. Если конфликтная ситуация реализуется ограниченное число раз, то рекомендации теории игр теряют смысл.
Игра – это упрощенная математическая модель конфликтной ситуации.
Игра ведется по определенным правилам. Суть игр состоит в том, что каждый участник принимает такое решение, которое, как он полагает, обеспечит ему наилучший исход. Исходом игры называется значение некоторой функции, называемой функцией выигрыша (платежной функцией), которая может задаваться в матричном или аналитическом виде.
|
|
|
Величина выигрыша зависит от стратегии, принимаемой игроком.
Стратегия – это совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игр.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш. Количество стратегий у каждого игрока может быть конечным или бесконечным. В зависимости от этого игры подразделяются на конечные и бесконечные.
Игра состоит из отдельных партий.
Партия – это каждый вариант реализации игры.
В партии игроки совершают ходы.
Ход – это выбор и реализация игроком одного из допустимых вариантов поведения.
В игре могут сталкиваться интересы двух или нескольких игроков, поэтому игры бывают парные и множественные. В зависимости от взаимоотношений участников различают игры некооперативные (бескоалиционные), когда участники имеют права заключать соглашения, и кооперативные (коалиционные).
В экономике нередко приходится сталкиваться с ситуацией, когда один из участников безразличен к результату игры. Такие игры называются играми с природой. Под термином «природа» понимают все совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решения.
Матричные игры. Равновесная ситуация.
Пусть в игре участвуют два игрока. Игрок 
имеет m стратегий, а игрок 
– n стратегий.
Обозначим стратегии игрока 
как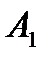 
, 
, …, 
, а стратегии игрока 
– как 
, 
, …, 
.
Если игрок 
выбрал стратегию 
, а игрок 
– стратегию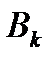 
, то выигрыш игрока составит 
, а игрока – 
, причем
= - 
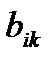. (4.1)
Поэтому при анализе такой игры достаточно рассмотреть выигрыш только одного игрока, например выигрыш игрока А. Зная выигрыш аik по формуле (4.1) легко определить выигрыш .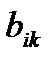
Матричные игры называются парными играми с нулевой суммой, в которых выигрыш одного игрока равен проигрышу другого.
|
|
|
Если известны все значения для каждой пары стратегий {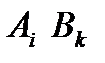 
}, 
= 1, 2, …, m, 
= 1, 2, …, n, то их удобно записать в виде прямоугольной таблицы, строки 
которой соответствуют стратегиям игрока , а столбцы – стратегиям игрока В (табл. 4.1).
Таблица 4.1
| 
| … | 
| |
…
| 
…
| 
…
| … … … … | 
…
|
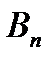
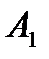
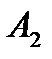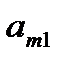
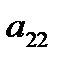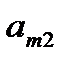
Чаще эти выигрыши записывают в виде платежной матрицы (матрицы игр) размера 
, поэтому такие игры называются матричными играми 
:
А= 
Матричные игры относятся к разряду антагонистических, т.е. игр, в которых интересы игроков противоположны.
Пример 4.1. Каждый из двух игроков 
и 
одновременно и независимо друг от друга записывают на листе бумаги любое целое число. Если записанные числа имеют одинаковую четность, то игрок 
выигрывает одно очко, если разные, то одно очко выигрывает игрок 
Построить платежную матрицу данной игры.
Решение. У игрока две стратегии: 
– записать четное число и 
– записать нечетное число. У игрока 
также две стратегии: 
– записать четное число и 
– записать нечетное число. Матрица выигрышей игрока в этой игре 2×2 имеет вид
= 
.
В данной матрице строки соответствуют стратегиям игрока 
, а столбцы – стратегиям игрока .
Действительно, если игрок делает ход 
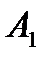, а игрок – ход 
, то одно очко выигрывает игрок и 
= 1. Если игрок делает ход 
, а игрок – ход 
, то одно очко выигрывает игрок , соответственно игрок 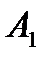это очко проигрывает, т.е. 
= -1 и т.д.
В примере 4.1 рассмотрена простейшая математическая модель конечной конфликтной ситуации, когда имеются два участника и выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой.
Равновесная ситуация
Пусть матричная игра m×n задана платежной матрицей
= (4.2)
Строки этой матрицы соответствуют стратегиям игрока , а столбцы – стратегиям игрока . В теории игр предполагается, что оба игрока действуют разумно, т.е. стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим для себя образом. Определим оптимальные стратегии каждого из игроков. Начнем с анализа стратегий игрока . На стратегию 
, игрока игрок ответит такой стратегией 
, при которой выигрыш игрока будет минимальным. Аналогично игрок B будет отвечать на все m стратегий игрока . Другими словами, найдем в каждой строке матрицы минимальный элемент (минимальные выигрыши игрока )
|
|
|
и запишем их в правом столбце табл. 4.2.
Таблица 4.2.
| 
| … | 
| … | 
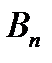
| Минимальные выигрыши игрока А | |
…
…
| 
| 
| 
| 
| 
| 
| 
|
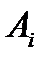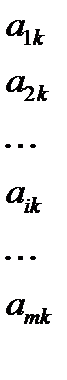
| Максимальные выигрыши игрока А | 
| 
| 
| 
| 
| 
|
Действуя разумно, игрок остановится на той стратегии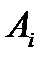 
, для которой 
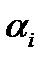окажется максимальным. Поэтому среди чисел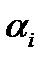
выбираем максимальное число
(4.3)
Число 
называется нижней ценой игры.
Принцип построения стратегии игрока , основанный на максимизации минимальных выигрышей, называется принципом максимина (maxmin).
Проведем анализ стратегий игрока 
. Для этого найдем в каждом столбце матрицы максимальный элемент (максимальные выигрыши игрока ):
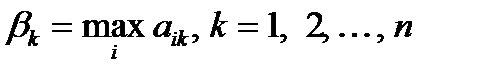
и запишем их в нижней строке табл. 4.2. Действуя разумно, игрок B остановится на той стратегии 
, для которой 
выбираем минимальное число
(4.4)
Число β называется верхней ценой игры.
Принцип построения стратегии игрока B, основанный на минимизации максимальных выигрышей, называется принципом минимакса (minmax).
Нижняя цена игра α и верхняя цена игра β связаны неравенством
α ≤ β. (4.5)
Если 
или
(4.6)
то ситуация 
оказывается равновесной, и ни один игрок не заинтересован в том, чтобы ее нарушить. В том случае, когда верхняя цена игры равна нижней, их называют просто ценой игры.
Если α=β, то такую игру называют также игрой с седловой точкой, а пара оптимальных стратегий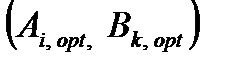 
– седловой точкой матрицы. Цена игры обозначается буквой v. Тогда 
.
Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.
Пример 4.2. Игроки и записывают одну из трех цифр: 1, 2 или 3. Затем сравнивают эти цифры и расплачиваются друг с другом так, как показано в платежной матрице размера 3×3:
= 
Определить оптимальные стратегии.
Решение. Здесь строки соответствуют стратегиям игрока , а столбцы – стратегиям игрока .
|
|
|
Стратегия игрока : 
; 
; 
.
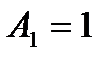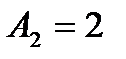Стратегия игрока : 
; 
; 
.
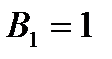Определим оптимальные стратегии каждого из игроков. Начнем с анализа стратегий игрока . Игрок анализирует свою стратегию на максимин (maxmin), т.е. на максимальный из своих минимальных выигрышей. На стратегию 
игрока игрок В ответит стратегией 
, т.е. то стратегией, при которой выигрыш игрока будет минимальным (выигрыш – 2 игрока означает его выигрыш +2). На стратегию 
игрока игрок В ответит стратегией 
(минимальный выигрыш игрока равен 1). На стратегию 
– стратегией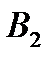 
(минимальный выигрыш игрока равен –3). Запишем минимальный выигрыш игрока А в правом столбце табл. 4.3.
Таблица 4.3.
| 
| 
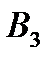
| Минимальные выигрыши игрока А | |
| -2 | -3 | -1 | -2 -3 |
| Максимальные выигрыши игрока А |
Игрок , проанализировав правый столбец таблицы, оставит свой выбор на стратегии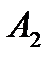 
, при которой его минимальный выигрыш максимален. Это максимальное значение называется максимин (maxmin). В данном случае maxmin = 1. Если игрок будет придерживаться этой стратегии, то ему гарантирован выигрыш, не менее 1, при любом поведении противника.
Аналогично проведем анализ стратегий игрока . Игрок В анализирует свою стратегию на минимакс (minmax), т.е. на минимальный из максимальных выигрышей игрока . На стратегию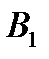 
игрока игрок ответит стратегией 
, т.е. той стратегией, при которой его выигрыш будет максимальным и равен 3. На стратегию 
игрока игрок ответит стратегией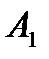 
(его максимальный выигрыш равен 2), на стратегию 
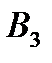– стратегией (его максимальный выигрыш равен 1). Запишем максимальные выигрыши игрока в нижней строке табл. 5.3. В данном случае minmax = 1. Если игрок В будет придерживаться этой стратегии, то он проиграет не больше 1 при любом поведении противника.
Таким образом, в рассматриваемой игре maxmin и minmax совпали:
maxmin =minmax = 1.
Таким образом, ситуация оказывается равновесной, матрица игры имеет седловую точку
.
|
|
|
