 |
Пример 16. 3. 4 задачи для самостоятельного решения
|
|
|
|
Пример 16
option explicit
dim a
'Программа определения количества бит в двоичном
'представлении целого положительного числа
a=Cint(InputBox(" Ввод числа", " Введите число типа INT", 0))
dim i 'параметр цикла
dim m
m=14
i=2^m
While ((a\i) and 1)< > 1
m=m-1
i=2^m
Wend
msgbox m+1
3. 4 ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Операторы цикла.
1. Вычислите множество значений функции y=x 52 0+b для аргумента х, изменяющегося от -10 до 10 с шагом 2, при b=5.
2. Вычислите k первых членов арифметической прогрессии, заданных следующим рекуррентным образом: a0 =1, an+1 =a n+2, где n=0, 1, 2,...
3. Вычислите произведение m членов арифметической прогрессии, если известны её первый член a1 и разность арифметической прогрессии h.
4. Найдите последовательность {a1, a2,..., a20 }, элементы которой вычисляются по формуле an=n/(n+1).
5. Вычислите значение n! для n=7. Ответ: 5040.
6. *Вычислить кубический корень из A с помощью применения итерационной формулы: 
. Начальное приближение выберите самостоятельно. Прекратите вычисления, если разность двух последовательных итераций станет меньше, чем произведение последнего приближения на 10-7.
7. Определите, существует ли такая четверка последовательных натуральных чисел, сумма квадратов которых равна сумме квадратов трёх следующих натуральных чисел.
8. Напишите программу вычисления при заданном х выражения:
Sin(x)+ Sin(Sin(x)) + Sin(Sin(Sin(x)))+…+Sin(Sin(…Sin(x)…))
n
9. Вычислите наибольший общий делитель натуральных чисел A и B.
10. Вычислите (1-1/22)·(1-1/32)·…· (1-1/n2), n> 2.
11. Вычислите cos(1+cos(2+ … +cos(39+cos40)... )).
12. Пусть k> 0 - целое число. Вычислите k-й член последовательности {xn},
|
|
|
где x0=1, xn=n·xn-1+1/n, n=1, 2, 3,...
13. Подсчитайте количество цифр в десятичной записи целого неотрицательного числа N.
14. Присвойте логической переменной T значение TRUE или FALSE в зависимости от того, является натуральное число k степенью 3 или нет.
15. Вычислите (2n-1)!! =1·3·5·…·(2n-1), n> 0.
Вычислите: 
16. Вычислите 1! +2! +3! +…+n!, для n> 1.
17. Числа Фибоначчи f n определяются итерационными формулами
f 0=f 1=1; f n=fn-1+f n-2, n=2, 3,... Определите десятое число Фибоначчи.
18. Числа Фибоначчи f n определяются итерационными формулами
f 0=f 1=1; f n=fn-1+f n-2, n=2, 3,... Найдите первое число Фибоначчи, большее заданного m, m> 1.
19. Вычислите sin(1)+sin(1. 1)+sin(1. 2)+ … +sin(2).
20. Вычислите сумму квадратов всех целых чисел, попадающих в интервал (ln(x), exp(x)), x> 1.
21. Присвойте логической переменной P значение TRUE, если целое n (n> 1) является простым числом, и значение FALSE - в противном случае.
22. Вычислите
23. Определите, является ли заданное натуральное число совершенным, т. е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 является совершенным числом, т. к. 6=1+2+3). Приведём ещё несколько совершенных чисел: 28, 496, 8128, 33550336, 8589869056. Отметим, что если сумма делителей числа больше самого числа, то такое число называется избыточным числом, если меньше - дефектным числом.
24. Дано целое n> 2. Найдите все простые числа из [2, n].
25. Найдите сумму цифр заданного натурального числа.
26. Определите натуральное число, получаемого выписыванием в обратном порядке цифр заданного натурального числа.
27. Определите, является ли заданное натуральное число палиндромом, т. е. таким натуральным числом, десятичная запись которого читается одинаково слева направо и справа налево.
28. Установите, верно ли, что все четыре цифры данного натурального числа n< 10000 различны?
29. Дано натуральное k. Напечатайте k-ю цифру последовательности 1234567891011121314..., в которой выписаны подряд все натуральные числа.
|
|
|
30. Дано натуральное k. Напечатайте k-ю цифру последовательности 149162536..., в которой выписаны подряд квадраты всех натуральных чисел.
31. Дано натуральное k. Напечатайте k-ю цифру последовательности 1123581321..., в которой выписаны подряд все числа Фибоначчи.
32. Не используя стандартные функции (за исключением Abs), вычислите с точностью Eps> 0 сумму функционального ряда 1+x/1! +x 2/2! + … +xn/n! +…. Считайте, что требуемая точность достигнута, если очередное слагаемое по модулю меньше Eps (все последующие слагаемые можно уже не учитывать).
33. Определите, в каких двузначных числах удвоенная сумма цифр равна их произведению?
Ответ: 36, 44, 63.
34. Найдите двузначное число, равное утроенному произведению его цифр.
Ответ: 15, 24.
35. Найдите двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.
Ответ: 27.
36. Найдите все трёхзначные числа, представимые в виде сумм факториалов своих цифр.
Ответ: 145.
37. Найдите все двузначные числа, сумма квадратов цифр которых делится на 17.
Ответ: 14, 28, 29, 35, 41, 53, 67, 76, 82, 92.
38. Найдите все трёхзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.
Ответ: 100, 147.
39. Найдите все трёхзначные числа, средняя цифра которых равна сумме первой и второй цифр.
40. Найдите все трехзначные числа, сумма цифр которых равна данному целому числу.
41. Найдите все делители числа 1234.
42. Найдите все двузначные числа, сумма цифр которых не меняется при умножении числа на 2, 3, 4, 5, 6, 7, 8, 9.
43. Даны целое число а и натуральное число n. Вычислите: a ·(а+1) ·... · (а+n-1).
44. Установите, можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел?
45. Найдите первую степень числа 3, превышающую данное целое число a.
46. Найдите наибольшую степень числа 2, делящую данное целое число a.
47. Проверьте, содержит ли квадрат данного натурального числа n цифру 3 в своей записи.
48. Приведите дробь вида a/b, b≠ 0, к несократимому виду.
49. Найдите среднее арифметическое последовательности целых чисел произвольной длины.
50. Найдите наименьшее положительное число x, удовлетворяющее условию 1+x> 1.
|
|
|
51. Письма-вызовы, содержащие предложение решить ряд трудных математических задач, были распространены в XVI-XVII вв. П. Ферма направил свой вызов математикам Франции, Голландии и Англии, в частности Дж. Валлису. П. Ферма в письме, названном " Первый вызов математикам" (3 января 1657 г), привёл следующие две задачи: (1) найти куб, который при добавлении всех его аликвотных частей дал бы квадрат. Например, число 343 есть куб со стороной 7. Все его аликвотные части это: 1, 7, 49; если их прибавить к самому 343, получится число 400, которое является квадратом со стороной. Найти другой куб с таким же свойством; (2) найти квадратное число, которое при прибавлении всех своих аликвотных частей составило бы кубическое число. Напишите программы, решающие указанные задачи.
52. Вычислите множество значений функции y для х, изменяющихся от -10 до 10 с шагом 2.
(a) y=x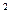 
+3x-1; (e) y= 
;
(b) y=2x+4; (f) y=x 
;
(c) y=x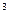 
-16x; (g) y= 
;
(d) y=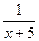 
;
|
|
|
