 |
4. 4 задачи для самостоятельного решения
|
|
|
|
Пример 2
' Имя файла Yes param. vbs
'Вывести на экран значение пяти введённых переменных, а также их 'удвоенную величину
option explicit
dim a, i
Sub print(x)
MsgBox i& " -е " & " Введённое число: " & x& ", удвоенное число: " & _
(2*x), vbInformation, " Результат: "
End Sub
For i=1 to 5
a=InputBox (" Введите число: ", " Окно ввода числа: " )
print a
Next
Пример 3
' Имя файла ByVal_sub. vbs
'Вывести на экран информацию о зарплате сотрудника с вычетом
'налога и без вычета, используя в программе процедуру
option explicit
dim a
Sub nalog(ByVal a)
a=a-(13*a)/100
MsgBox " Зарплата с вычетом налога: " & a
End Sub
a=InputBox (" Введите вашу зарплату без вычета налога: ", " Окно ввода: " )
nalog a
MsgBox " Зарплата без вычета налога: " & a
Пример 4
' Имя файла rasstoyanie. vbs
'Совместное использование функции и процедуры
'Определение расстояния, пройденного физическим телом
option explicit
dim v, t, a
'--------------
Function Rasst(x, y, z)
rasst=x*y+z*y*y/2
end function
'--------------
Sub Input(param, x)
x=inputbox(" Введите значение параметра " & param, _
" Окно ввода " & param, " 0" )
end sub
'--------------
msgbox " Задача: " & vbcrlf& _
" Определить расстояние пройденное физическим телом" & VbCrLf& _
" за время t, со скоростью v, с ускорением a", vbInformation
input " скорости", v
input " времени", t
input " ускорениия", a
Msgbox " Тело прошло расстояние " & rasst(v, t, a), vbExclamation
Пример 5
' Имя файла style. vbs
'Демонстрация стиля программирования, который называется
'процедурным программированием
option explicit
dim a, b
Sub input(x)
'ввод значения переменной
x=InputBox (" Введите переменную: ", " Окно ввода переменной: " )
End Sub
|
|
|
Sub change(x, y)
Dim z
'обмен значениями двух переменных a и b
z=x
x=y
y=z
End Sub
Sub output (x, y)
'вывод значений переменных
MsgBox " Переменные после обмена значениями: a = " & x& ", b = " & _
y, vbInformation, " Результат: "
End Sub
'Процедурный стиль программирования состоит
'просто в последовательном вызове процедур
input a
input b
change a, b
output a, b
см. также примеры в каталоге лаб. раб 4
4. 4 ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Видоизмените программу демонстрационного примера, чтобы она печатала следующее:
***********************************************************
Санкт-Петербург
Набережная р. Мойки, 48, РГПУ
***********************************************************
Воспользуйтесь функцией для печати нужного количества пробелов.
2. Напишите программу нахождения всех корней биквадратного уравнения.
3. Напишите программу вычисления P по формуле:
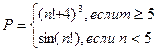
4. Напишите программу вычисления
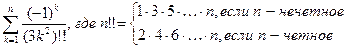
5. Проверьте, делится ли заданное натуральное число на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, делится на 19.
6. Вычислите max(min(3, 5), min(2, 6)).
7. Задача Ферма. Найдите квадрат, который в сумме со всеми его собственными делителями дает куб.
8. Вычислите (результат принадлежит Сринивазу Рамануджану).
Ответ: 3
9. Вычислите (результат принадлежит Сринивазу Рамануджану)
, где знаки перед корнями периодически повторяются группами по три: " -", " +", " -".
Ответ: 
10. Вычислите (результат принадлежит Сринивазу Рамануджану)
где знаки перед корнями периодически повторяются группами по три: " -", " +", " -".
Ответ: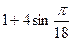 
11. Вычислите (результат принадлежит Сринивазу Рамануджану)
где знаки перед корнями периодически повторяются группами по три: " -", " +", " +".
|
|
|
Ответ: 
12. Замечательным достижением Франсуа Виеты является введение в математику задачи о нахождении бесконечного произведения. Вычислите
Разумеется, Виета не доказывает сходимости полученного бесконечного произведения, будучи интуитивно уверенным в справедливости своего предельного утверждения.
Ответ: 
13. По вещественному x вычислите значение функции
sh(x)· tg(x+1)-tg2(2+sh(x-1))
14. Опишите функцию Stepen(x, n), зависящую от вещественного x и натурального n и вычисляющую (посредством умножения) величину xn, и используйте её для вычисления значения выражения 2. 7k+(a+1)-5.
15. Даны три натуральных числа. Определите их наибольший общий делитель.
16. Даны отрезки a, b, c и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, найдите площадь данного треугольника. Определите процедуру Plo(x, y, z), определяющую площадь треугольника со сторонами x, y и z, если такой треугольник существует.
17. Опишите процедуру Socr(a, b, p, q), зависящую от целых параметров (b≠ 0), которая приводит дробь 
к несократимому виду 
.
18. Пусть процедура Socr(a, b, p, q), зависящая от целых параметров (b-0), приводит дробь к несократимому виду . Опишите данную процедуру и использовать ее для приведения дроби 1+1/2+1/3+…+1/20 к несократимому виду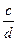 
.
19. Пусть процедура MaxMin(x, y) присваивает параметру x большее из вещественных чисел x и y, а параметру y - меньшее. Опишите данную процедуру и используйте её для перераспределения значений вещественных переменных a, b и c так, чтобы выполнилось a≥ b≥ c.
20. Даны длины a, b и c сторон треугольника. Найдите медианы треугольника, сторонами которого являются медианы исходного треугольника.
Указание. Длина медианы, проведённой к стороне a, равна
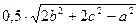
21. Опишите функцию F(m, n)=n! m! /(n+m)!, где n и m - неотрицательные целые числа.
22. Даны координаты вершин двух треугольников. Определите, какой из них имеет большую площадь.
23. Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найдите расстояние от данной точки до ближайшей стороны треугольника. (При определении расстояний учесть, что площадь треугольника вычисляется и через три его стороны, и через основание и высоту. )
24. Три прямые на плоскости заданы уравнениями akx+bky=ck, k=1, 2, 3. Если эти прямые попарно пересекаются и образуют треугольник, то найдите его площадь.
|
|
|
25. Найдите наименьшее общее кратное четырех заданных натуральных чисел.
26. Два простых числа называются близнецами, если они отличаются друг от друга на 2 (таковы, например, числа 41 и 43). Найдите все пары чисел-близнецов из отрезка [n, 2n], где n - заданное натуральное число, большее двух, с помощью функции распознавания простых чисел. Приведём несколько примеров чисел-близнецов: (5, 7), (11, 13), (17, 19), (22271, 22273).
27. Два натуральных числа называются дружественными числами, если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284, известные ещё Пифагору). Найдите все пары " дружественных" чисел, не превосходящих заданного натурального числа. Приведём ещё несколько примеров дружественных чисел: 1184 и 1210 (Н. Паганини), 17296 и 18416 (П. Ферма), 9363584 и 9437056 (Р. Декарт).
28. Задача Ферма. Найдите куб, который в сумме со всеми его собственными делителями дает квадрат.
29. Дано чётное число n> 2. Проверьте для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое чётное n, большее двух, представляется в виде суммы двух простых чисел. Воспользуйтесь функцией распознавания простых чисел.
30. Дано натуральное число n. Выясните, является ли оно квадратом. Определите функцию, позволяющую распознавать квадраты.
31. Даны натуральное число n. Выясните, является ли оно степенью пятерки. Определите функцию, позволяющую распознавать степени пятерки.
32. Дано натуральное число n. Выясните, является ли оно простым. Определите функцию, позволяющую распознавать простые числа.
33. Даны три натуральных числа. Определите их наибольший общий делитель.
34. Числа Фибоначчи u0, u1, u2,... определяются следующим образом: u0=1, u1=2,
un=un-1+un-2 (n=2, 3,... ). Напишите функцию, вычисляющую un для данного неотрицательного целого n.
35. В XX в. математики обобщили понятие " дружественные числа" и занялись поиском общительных чисел - замкнутых циклов из трёх и более чисел. Например, в тройке чисел (1945330728960, 2324196638720, 2615631953920) делители первого числа в сумме дают второе число, делители второго в сумме дают третье число, а делители третьего числа в сумме дают первое число. Самый длинный из известных циклов [Сингх, 2000, с. 68] состоит из 28 общительных чисел, первое из которых равно 14316. Напишите функцию, устанавливающую, являются ли три заданные натуральные числа общительными числами.
|
|
|
|
|
|
