 |
Нормальная коническая проекция Птолемея
|
|
|
|
Проекция предложена ученым Птолемеем во IIвеке н. э. Она строится на касательном конусе. Масштаб не искажается на всех меридианах и на параллели касания с широтой φ0. Искажения невелики и в полосе карты, ограниченной параллелями, отстоящими на 15° к северу и к югу от параллели касания.
Картографическая сетка создается геометрическим построением. После развертывания конуса в плоскость параллель касания с широтой φ0 изобразится дугой окружности, радиус которой (р0) равен расстоянию от вершины конуса до параллели касания: р0 = АВ (рисунок 19).
Радиус параллели касания можно рассчитать по формуле:
 .
.
Все остальные параллели у этой сетки тоже дуги окружностей с центром в точке А. Расстояние а между параллелями (рисунок 15) равно:
 ,
,
где φ0– широта параллели касания; ∆φ – разность широт соседних параллелей;R= 6 371 км; М – знаменатель масштаба.
Меридианы в этой проекции имеют форму прямых линий, сходящихся в точке А под равными углами γ (рисунок 19). Угол γ не равен ∆λ. Это связано с тем, что окружность касания на эллипсе при развертывании конуса на плоскость превращается лишь в дугу окружности, т. е. ее угол уменьшается. Угол γ между меридианами равен:
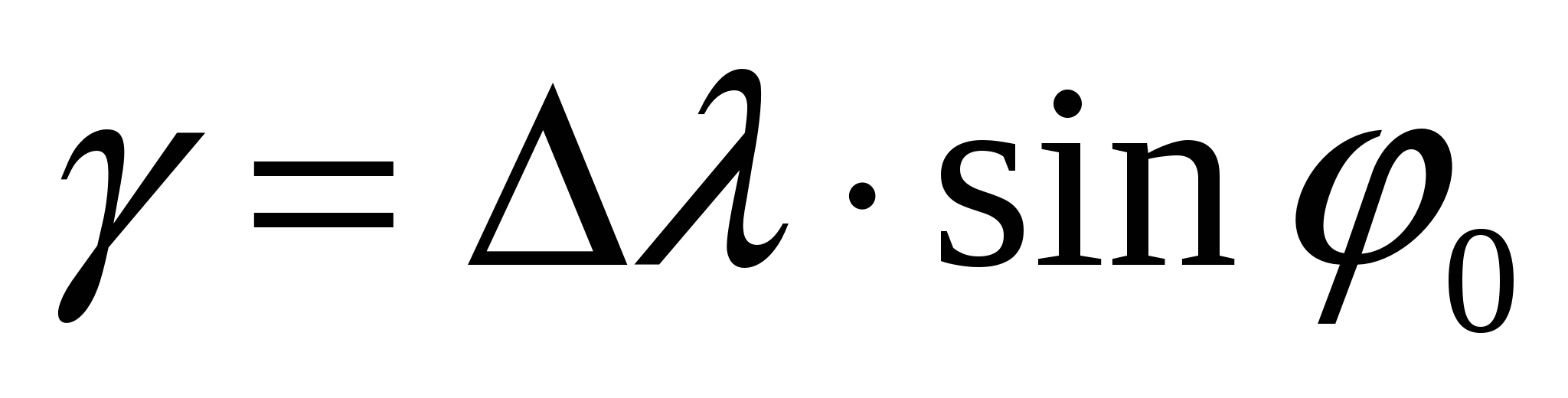 .
.
На чертеже выбирается точка А, которая является центром дуг всех параллелей Первой строится параллель касания с широтой φ0, в нашем случае φ0= 50°.
Радиус этой параллели равен:
 .
.
Расстояние а между параллелями будет равно:
 .
.

Рисунок 19 – Коническая проекция Птолемея
Таким образом, радиусы соседних параллелей будут различаться на 1,1 см. Радиус параллели 60° составит 4,3 см (эта параллель ближе к центру), а радиус параллели 40° – 6,5 см.
Угол γ между меридианами равен:
|
|
|
 .
.
Радиально расходящиеся прямые под углом 7,7º из точки А и будут являться меридианами.
Цилиндрическая прямоугольная проекция
В этой проекции для проектирования берется секущий цилиндр. Главный масштаб сохраняется на двух параллелях сечения, а также на всех меридианах. Расстояния между меридианами равны действительным дугам параллели сечения с широтой φ0.
Картографическая сетка – взаимно перпендикулярные линии, образующие при пересечении прямоугольники со сторонами с и d (рисунок 17).
Расстояния с и d рассчитываются по формулам:
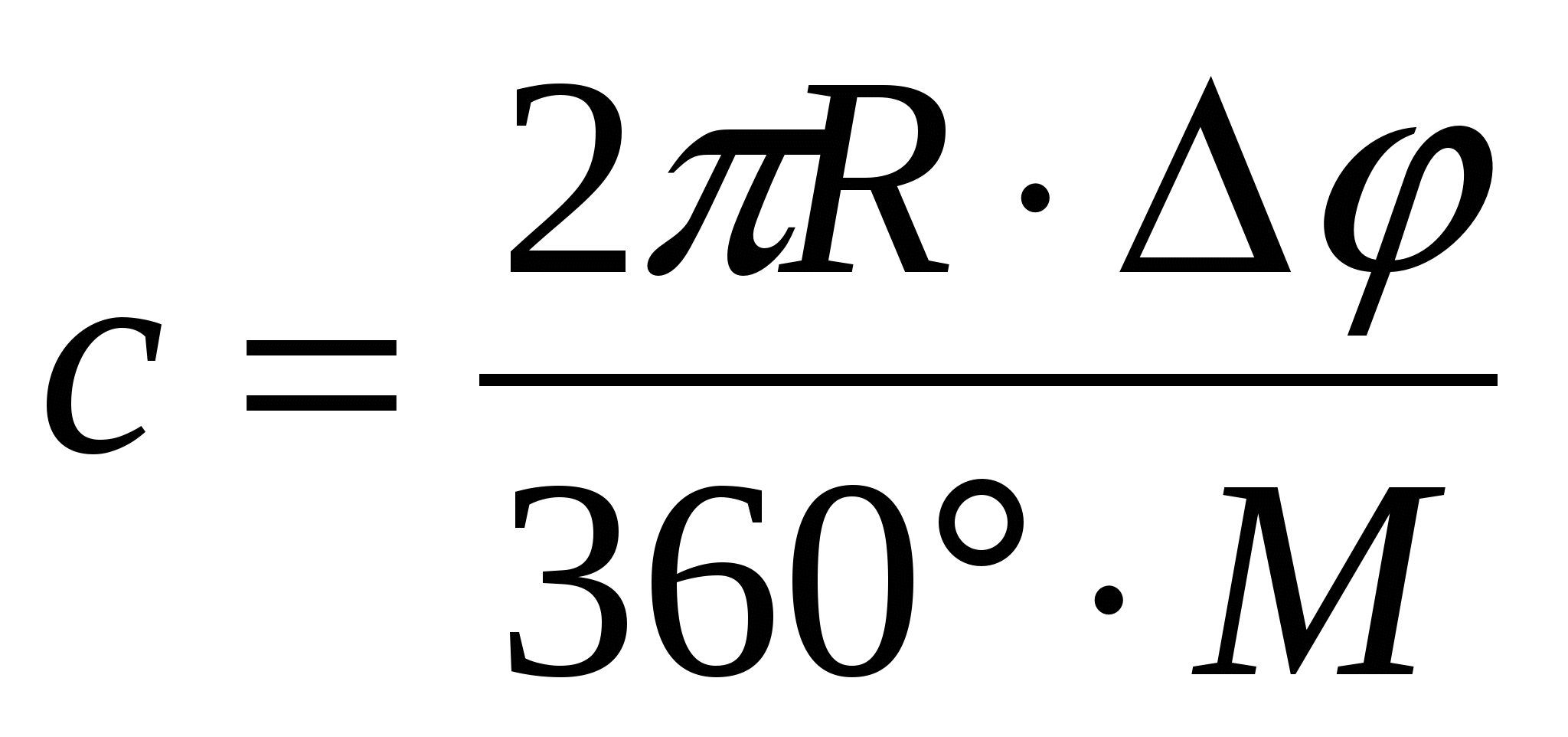 ,
,
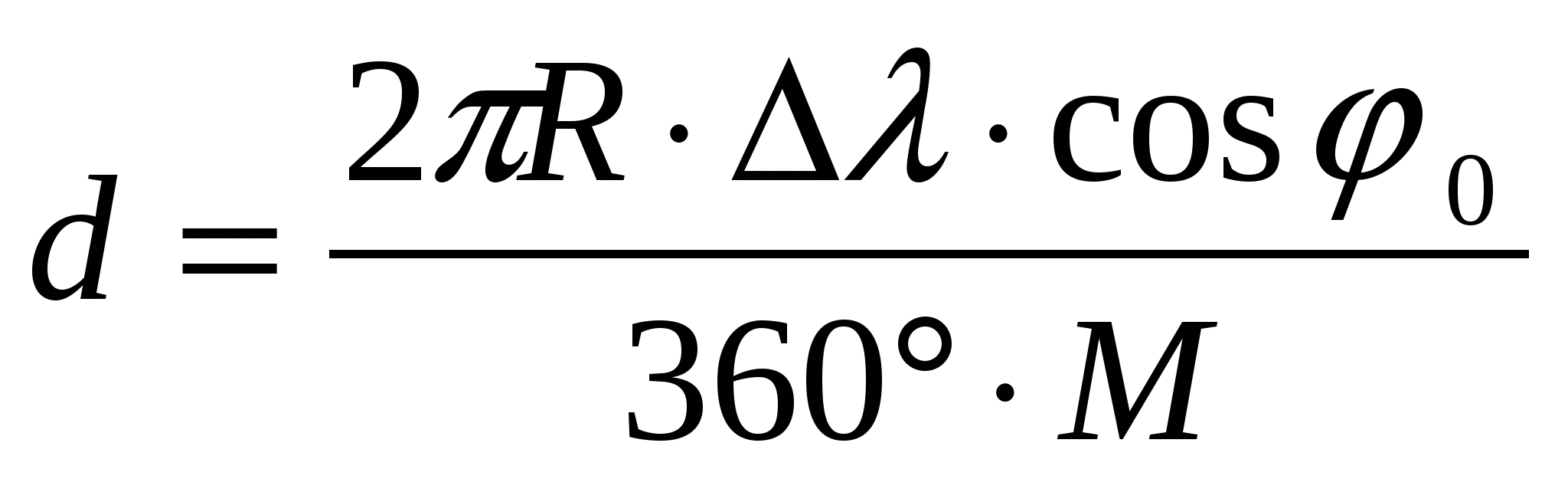 ,
,
где R= 6 371 км (средний радиус Земли); ∆φ – разница широт соседних параллелей; ∆λ – разница долгот соседних меридианов; М – знаменатель масштаба; φ0– широта сечения.
Если же  , то
, то  .
.

Рисунок 17 – Картографическая сетка в цилиндрической
прямоугольной проекции
Пример вычисления с и d,если φ0= 50; ∆φ = ∆λ = 10º; масштаб 1: 100 000 000 (знаменатель – 1000 км/см). Вычисляем величину с по формуле:
 .
.
Проекция Аитова- Гаммера.
Проекция Гаммера-Аитова - это модифицированная Равновеликая азимутальная проекция Ламберта.
МЕТОД ПРОЕЦИРОВАНИЯ
Видоизмененная азимутальная проекция. Центральный меридиан представляет собой прямую линию, длиной в половину длины экватора. Другие меридианы представляют собой сложные кривые, выгнутые по направлению от центрального меридиана и расположенные через неравные интервалы вдоль экватора. Экватор представлен прямой линией, все другие параллели представлены сложными кривыми, выгнутыми по направлению от ближайшего полюса и расположенными через неравные интервалы вдоль центрального меридиана.
ТОЧКА КАСАНИЯ Пересечение центрального меридиана с экватором. ЛИНЕЙНЫЕ ЭЛЕМЕНТЫ КАРТОГРАФИЧЕСКОЙ СЕТКИ
Только Экватор и центральный меридиан являются прямыми линиями.
СВОЙСТВА Форма
Искажение возрастает при удалении от начала координат.
|
|
|
Площадь
Равновеликая проекция.
Направление
Локальные углы являются истинными только в центре.
Расстояние
Масштаб уменьшается вдоль экватора и центрального меридиана по мере удаления от начала координат.
|
|
|


